
题目列表(包括答案和解析)
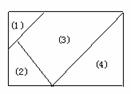
7.用五种不同的颜色,给图中的(1)(2)(3)(4)的各部分涂色,每部分涂一色,相邻部分涂不同色,则涂色的方法共有几种?
6.20个不加区别的小球放入编号为1、2、3的三个盒子中,要求每个盒内的球数不小于它的编号数,求不同的放法种数.
5.有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数.
(1)全体排成一行,其中甲只能在中间或者两边位置.
(2)全体排成一行,其中甲不在最左边,乙不在最右边.
(3)全体排成一行,其中男生必须排在一起.
(4)全体排成一行,男、女各不相邻.
(5)全体排成一行,男生不能排在一起.
(6)全体排成一行,其中甲、乙、丙三人从左至右的顺序不变.
(7)排成前后二排,前排3人,后排4人.
(8)全体排成一行,甲、乙两人中间必须有3人.
4.二次函数y=ax2+bx+c的系数a、b、c,在集合{-3,-2,-1,0,1,2,3,4}中选取3个不同的值,则可确定坐标原点在抛物线内部的抛物线多少条?
3.某人手中有5张扑克牌,其中2张为不同花色的2,3张为不同花色的A,有5次出牌机会,每次只能出一种点数的牌但张数不限,此人有多少种不同的出牌方法?
2.圆周上有2n个等分点(n>1),以其中三个点为顶点的直角三角形的个数为_________.
1.从集合{0,1,2,3,5,7,11}中任取3个元素分别作为直线方程Ax+By+C=0中的A、B、C,所得的经过坐标原点的直线有_________条(用数值表示).
本章内容相对独立性较强,并且密切联系实际应用性较强,分为四个部分:排列组合、二项式定理、概率和概率统计。具有概念性强灵活性强,思维方法新颖等特点,要注意从加深对概念的理解和掌握内在联系与区别方面下功夫,四部分中,排列、组合是基础和工具。
本章主要的数学思想有:化归思想,比较分类思想,极限思想和模型化思维方法。学习时应注意发散思维和逆向思维,通过分类分步把复杂问题分解恰当地应用集合观点、整体思想,从全集、补集等入手,使问题简化。
[例题]
[例1] 四名优等生保送到三所学校去,每所学校至少得一名,则不同的保送方案的总数是_________.
解法一:分两步:先将四名优等生分成2,1,1三组,共有C 种;而后,对三组学生安排三所学校,即进行全排列,有A33种.依乘法原理,共有N=C
种;而后,对三组学生安排三所学校,即进行全排列,有A33种.依乘法原理,共有N=C
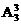 =36(种).
=36(种).
解法二:分两步:从每个学校至少有一名学生,每人进一所学校,共有A 种;而后,再将剩余的一名学生送到三所学校中的一所学校,有3种.值得注意的是:同在一所学校的两名学生是不考虑进入的前后顺序的.因此,共有N=
种;而后,再将剩余的一名学生送到三所学校中的一所学校,有3种.值得注意的是:同在一所学校的两名学生是不考虑进入的前后顺序的.因此,共有N=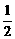 A
A ·3=36(种).
·3=36(种).
答案:36
[例2] 有五张卡片,它们的正、反面分别写0与1,2与3,4与5,6与7,8与9,将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
解:(间接法):任取三张卡片可以组成不同三位数C ·23·A
·23·A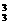 (个),其中0在百位的有C
(个),其中0在百位的有C ·22·A
·22·A (个),这是不合题意的,故共有不同三位数:C
(个),这是不合题意的,故共有不同三位数:C ·23·A
·23·A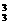 -C
-C ·22·A
·22·A =432(个).
=432(个).
[例3] 在∠AOB的OA边上取m个点,在OB边上取n个点(均除O点外),连同O点共m+n+1个点,现任取其中三个点为顶点作三角形,可作的三角形有( )

解法一:第一类办法:从OA边上(不包括O)中任取一点与从OB边上(不包括O)中任取两点,可构造一个三角形,有C C
C 个;第二类办法:从OA边上(不包括O)中任取两点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C
个;第二类办法:从OA边上(不包括O)中任取两点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C C
C 个;第三类办法:从OA边上(不包括O)任取一点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C
个;第三类办法:从OA边上(不包括O)任取一点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C C
C 个.由加法原理共有N=C
个.由加法原理共有N=C C
C +C
+C C
C +C
+C C
C 个三角形.
个三角形.
解法二:从m+n+1中任取三点共有C 个,其中三点均在射线OA(包括O点),有C
个,其中三点均在射线OA(包括O点),有C 个,三点均在射线OB(包括O点),有C
个,三点均在射线OB(包括O点),有C 个.所以,个数为N=C
个.所以,个数为N=C -C
-C -C
-C 个.
个.
答案:C
[例4]
函数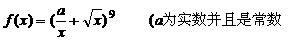 )
)
(1)已知 的展开式中
的展开式中 的系数为
的系数为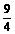 ,求常数
,求常数
(2)是否存在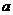 的值,使
的值,使 在定义域中取任意值时,
在定义域中取任意值时, 恒成立?如存在,求出
恒成立?如存在,求出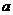 的值,如不存在,说明理由.
的值,如不存在,说明理由.
解(1)Tr+1=C 由
由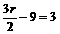 解得
解得

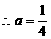
(2) 要使(
要使(
只需
10当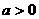 时,设
时,设
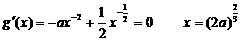
 |
(0, |
 |
(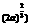 ,+ ,+ ) ) |
 |
- |
0 |
+ |
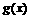 |
 |
极小值 |
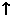 |
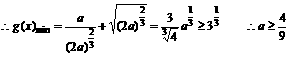
20当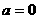 时,不成立 30当
时,不成立 30当 时,不成立 故当
时,不成立 故当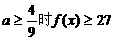
另解法
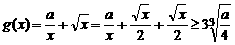 只需
只需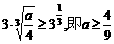
[例5] 五人站成一列,重新站队时,各人都不站在原来的位置上,有多少种站法?
解:设原来站在第i个位置的人是 (i=1,2,3,4,5)。重新站队时,
(i=1,2,3,4,5)。重新站队时, 站在第2
站在第2
个位置的站法有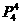 种,其中不符合要求的有:
种,其中不符合要求的有: 站第3位的
站第3位的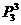 种,
种, 站第4位的
站第4位的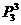 种,但有的站法在考虑
种,但有的站法在考虑 的情形时已经减去了,故只应再算(
的情形时已经减去了,故只应再算( )种,同理,
)种,同理, 站第5位的应再算[
站第5位的应再算[ ]种。
]种。 站在第3,4,5位的情形与站在第2位的情形时对等的,故所有符合要求的站法有:
站在第3,4,5位的情形与站在第2位的情形时对等的,故所有符合要求的站法有:
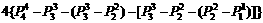 =44(种)
=44(种)
[例6] 一个口袋内装有4个不同的红球,6个不同的白球,若取出一个红球记2分,取出一个白球记1分,从口袋中取5个球,使总分不小于7分的取法有多少种?
解:设取 个红球,
个红球, 个白球,于是:
个白球,于是:
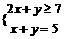 ,其中
,其中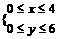 ,
,

因此所求的取法种数是: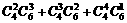 =186(种)
=186(种)
[例7]
已知数列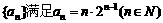 ,是否存在等差数列
,是否存在等差数列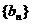 ,使
,使 对一切自然数n都成立?并证明你的结论。
对一切自然数n都成立?并证明你的结论。
解:假设满足要求的等差数列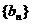 存在,由于所给等式对一切自然数n均成立,故当n=1,2,3时等式成立,从而可解得
存在,由于所给等式对一切自然数n均成立,故当n=1,2,3时等式成立,从而可解得 =1,
=1, =2,
=2, =3,因此若满足要求的等差数列存在,则必须是
=3,因此若满足要求的等差数列存在,则必须是 =n。.然后再证明当
=n。.然后再证明当 =n时所给等式确实成立即可。答案是肯定的。
=n时所给等式确实成立即可。答案是肯定的。
[例8]
若某一等差数列的首项为 ,其中m是
,其中m是 -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
解:由已知得: 。
。
注意到 ,从而等差数列的通项公式是:
,从而等差数列的通项公式是: ,设其前k项之和最大,则
,设其前k项之和最大,则
 ,解得k=25或k=26,故此数列的前25项之和与前26项之和相等且最大,
,解得k=25或k=26,故此数列的前25项之和与前26项之和相等且最大,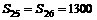 。
。
[例9]
已知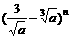 的展开式的各项系数之和等于
的展开式的各项系数之和等于 展开式中的常数项,求
展开式中的常数项,求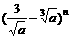 展开式中含
展开式中含 的项的二项式系数。
的项的二项式系数。
解:先求出 的常数项是27,从而可得
的常数项是27,从而可得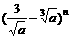 中n=7,对于
中n=7,对于 由二项展开式的通项公式知,含
由二项展开式的通项公式知,含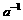 的项是第4项,其二项式系数是35。
的项是第4项,其二项式系数是35。
[例10]
求证: 能被25整除。
能被25整除。
解:注意到 即可。
即可。
[排列、组合与二项式定理练习1]
排列与组合是高中数学中从内容到方法都比较独特的一个组成部分,是进一步学习概率论的基础知识,该部分内容,不论其思想方法和解题都有特殊性,概念性强,抽象性强,思维方法新颖,解题过程极易犯“重复”或“遗漏”的错误,并且结果数目较大,无法一一检验,因此给考生带来一定困难。解决问题的关键是加深对概念的理解,掌握知识的内在联系和区别,科学周全的思考、分析问题。
二项式定理是进一步学习概率论和数理统计的基础知识,把握二项展开式及其通项公式的相互联系和应用是重点。
概率则是概率论入门,目前的概率知识只是为进一步学习概率和统计打好基础,做好铺垫。学习中要注意基本概念的理解,要注意与其他数学知识的联系,要通过一些典型问题的分析,总结运用知识解决问题的思维规律。
纵观近几年高考,排列、组合、二项式定理几乎每年必考,考题多以选择题、填空题出现,题小而灵活,涉及知识点都在两三个左右,综合运用排列组合知识,分类计数和分步计数原理;二项式定理及二项式系数的性质计算或论证一些较简单而有趣的小题也在高考题中常见。
新教材中增添了“概率”及“概率统计”的内容,从近几年新课程卷高考来看,每年都有一道解答题,占12分左右,今年在此处出题可能性也较大。
14、会用样本频率分布去估计总体分布。了解线性回归的方法和简单应用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com