
题目列表(包括答案和解析)
3.集合A=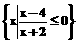 ,集合B=
,集合B=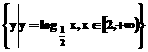 ,则
,则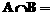 ______________.
______________.
1.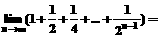 ___________.
___________.
2已知函数
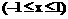 ,则
,则 __________.
__________.
2. 由经验得,在某超市的付款处排队等候付款的人数及其概率如下:
|
排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
|
概 率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
求:(1)至多有2个人排队的概率;
(2)至少有2人排队的概率.
.(1)设没有人排除为事件A,1个人排队为事件B,2个人排队为事件C,则P(A)=0.1, P(B)=0.16, P(C)=0.3,依题意A、B、C彼此互斥,所以至多2个人排队的概率为:
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)设至少2个人排队为事件D,则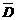 为至多1个人排队,即
为至多1个人排队,即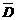 =A+B,因此
=A+B,因此
P(D)=1-P(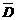 )=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
)=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
3用长为16米的篱笆,借助墙角围成一个矩形ABCD(如图),在P处有一棵树与两墙的距离分别为a米(0<a<12 )和4米。若此树不圈在矩形外,求矩形ABCD面积的最大值M.
解:设AB=x,则AD=16-x
,依题意得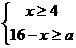 ,即
,即 
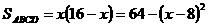
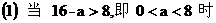 ,
,
 上是增函数,
上是增函数,
所以 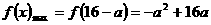 ,故
,故 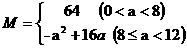
1. 某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为k(k>0),贷款的利率为4.8%,假设银行吸收的存款能全部放贷出去.
(Ⅰ)若存款利率为x,x∈(0,0.048),试写出存款数量g(x)及银行应支付给储户的利息h(x)与存款利率x之间的关系式;
(Ⅱ)问存款利率为多少时,银行可获得最大收益?
解析:(Ⅰ)由题意知,存款量g(x)=kx,银行应该支付的利息h(x)=xg(x)=kx2,x∈(0,0.048).
(Ⅱ)设银行可获得收益为y,则y=0.048kx-kx2=-k(x-0.024)2+0.0242k,
当x=0.024时,y有最大值,∴存款利率定为0.024时,银行可获得最大收益.
6. 已知甲袋中放有编号分别为0,0,1,3的四个红色小球,乙袋中放有编号为0,1,3,3,的四个黄色小球,丙袋中放有编号为1,3,3,3的四个兰色小球,现从中随机摸出红, 黄,兰色小球各一个,求 (1)摸出三个小球的编号相同的概率; (2)摸出小球的编号和不小于7的概率.
解(1)三个小球编号相同的概率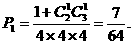
(2)三个小球的编号和不小于7的概率
7某厂使用两种零件A、B装配两种产品P、Q,该厂的生产能力是月产P产品最多有2500件,月产Q产品最多有1200件;而且组装一件P产品要4个A、2个B,组装一件Q产品要6个A、8个B,该厂在某个月能用的A零件最多14000个;B零件最多12000个 已知P产品每件利润1000元,Q产品每件2000元,欲使月利润最大,需要组装P、Q产品各多少件?最大利润多少万元.
7解 设分别生产P、Q产品x件、y件,则有
设分别生产P、Q产品x件、y件,则有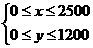 ,
, ,
,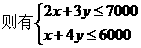 ,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
∴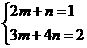 , ∴
, ∴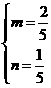 ,有x+2y=
,有x+2y=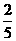 (2x+3y)+
(2x+3y)+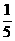 (x+4y)≤
(x+4y)≤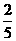 ×7000+
×7000+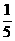 ×6000. 当且仅当
×6000. 当且仅当 解得
解得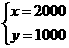 时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元).
时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元).
另外此题可运用“线性规划模型”解决. (万元/百台)=240(元/台).
8某外商到一开放区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.
(1)若扣除投资及各种经费,则从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,有两种处理方案 ①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
8解 由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为f(n),则f(n)=50n–[12n+
由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为f(n),则f(n)=50n–[12n+ ×4]–72=–2n2+40n–72
×4]–72=–2n2+40n–72
(1)获纯利润就是要求f(n)>0,∴–2n2+40n–72>0,解得2<n<18. 由n∈N知从第三年开始获利.
(2)①年平均利润= =40–2(n+
=40–2(n+ )≤16. 当且仅当n=6时取等号. 故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128.
)≤16. 当且仅当n=6时取等号. 故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128.
当n=10时,f(n)|max=128. 故第②种方案共获利128+16=144(万美元).
故比较两种方案,获利都是144万美元,但第①种方案只需6年,而第②种方案需10年,故选择第①种方案.
4 创新试题
5.已知某公司生产品牌服装的年固定成本是10万元,每生产千件,须另投入2.7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且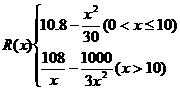 (1)写出年利润W(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大? (注:年利润=年销售收入-年总成本)
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大? (注:年利润=年销售收入-年总成本)
解:(1)当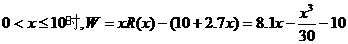
当
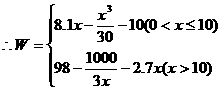
(2)①当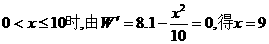
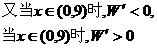
当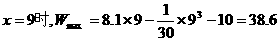
②当x>10时 
当且仅当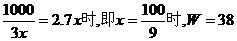
由①②知,当x=9千件时,W取最大值38.6万元.
4. 已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位小时)的函数,记作y=f(t),下表是某日各时的浪高数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1. 5 |
1. 0 |
0. 5 |
1. 0 |
1.49 |
1 |
0. 51 |
0.99 |
1.5 |
经长期观测y=f(t)的曲线可近似地看成函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8 00至晚上20
00至晚上20 00之间,有多少时间可供冲浪者进行运动.
00之间,有多少时间可供冲浪者进行运动.
4解 (1)由表中数据,知T=12,ω=
(1)由表中数据,知T=12,ω=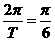 . 由t=0,y=1. 5得A+b=1. 5.
. 由t=0,y=1. 5得A+b=1. 5.
由t=3,y=1. 0,得b=1. 0. 所以,A=0. 5,b=1. 振幅A= ,∴y=
,∴y=
(2)由题意知,当y>1时,才可对冲浪者开放. ∴ >1,
>1, 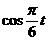 >0. ∴2kπ-
>0. ∴2kπ-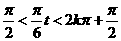 ,即有12k–3<t<13k+3. 由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24. ∴在规定时间内有6个小时可供冲浪者运动即上午9
,即有12k–3<t<13k+3. 由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24. ∴在规定时间内有6个小时可供冲浪者运动即上午9 00至下午15
00至下午15 00.
00.
3. 我校现有教职员工500人,为了开展迎2008奥运全民健身活动,增强教职员工体质,学校工会鼓励大家积极参加晨练与晚练,每天清晨与晚上定时开放运动场、健身房和乒乓球室,约有30%的教职员工坚持每天锻炼. 据调查统计,每次去户外锻炼的人有10%下次去室内锻炼,而在室内锻炼的人有20%下次去户外锻炼. 请问,随着时间的推移,去户外锻炼的人数能否趋于稳定?稳定在多少人左右?
解:设第n次去户外锻炼的人数为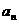 ,去室内锻炼的人为
,去室内锻炼的人为 ,则有:
,则有: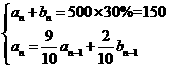 ,
, ,
,
 ,
,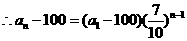 ,
,
 ∴
∴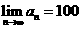 ,
,
∴随着时间的推移,去户外锻炼的人数将稳定在100人左右 。
2. 某工厂拟建一座平面图(如图所示)为矩形且面积为200m2 的三级污水处理池,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).
(1)写出总造价y(元)与污水处理池长x (m)的函数关系式f(x);
(2)若由于地形限制,长、宽都不能超过16m,求f(x)的定义域;
(3)在条件(2)下,污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价.
解析:①因污水处理水池的长为
 .
.
由题设条件 即函数定义域为[12.5,16]
即函数定义域为[12.5,16]
②先研究函数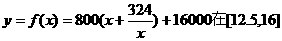 上的单调性,
上的单调性,
对于任意的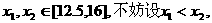
则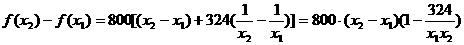
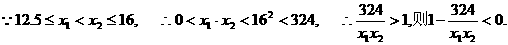
又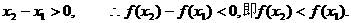
故函数y=f(x)在[12.5,16]上是减函数. ∴当x=16时,y取得最小值,此时

综上,当污水处理池的长为16m,宽为12.5m时,总造价最低,最低为45000元.
1. 要建一间地面面积为20 ,墙高为
,墙高为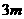 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元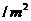 ,其余三面的造价为200元
,其余三面的造价为200元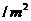 ,屋顶的造价为250元
,屋顶的造价为250元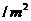 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
解:设地面矩形在门正下方的一边长为 ,则另一边的长为
,则另一边的长为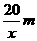 ,设总造价为
,设总造价为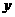 元,则
元,则
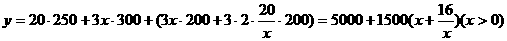
因为  ,当且仅当
,当且仅当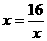 (
( 即
即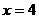 时 取“=”,所以,当
时 取“=”,所以,当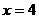 时
时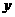 有最小的值
有最小的值 此时
此时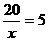 ,
,
答:当储藏室地面矩形在门正下方的一边长为 ,另一边的长为
,另一边的长为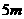 时,能使总造价最低造价为17000元。
时,能使总造价最低造价为17000元。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com