
题目列表(包括答案和解析)
2. 某工厂拟建一座平面图(如图所示)为矩形且面积为200m2 的三级污水处理池,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).
(1)写出总造价y(元)与污水处理池长x (m)的函数关系式f(x);
(2)若由于地形限制,长、宽都不能超过16m,求f(x)的定义域;
(3)在条件(2)下,污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价.
解析:①因污水处理水池的长为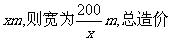
 .
.
由题设条件 即函数定义域为[12.5,16]
即函数定义域为[12.5,16]
②先研究函数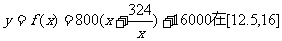 上的单调性,
上的单调性,
对于任意的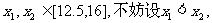
则
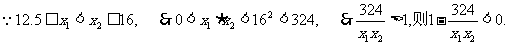
又
故函数y=f(x)在[12.5,16]上是减函数. ∴当x=16时,y取得最小值,此时
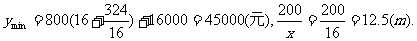
综上,当污水处理池的长为16m,宽为12.5m时,总造价最低,最低为45000元.
1. 要建一间地面面积为20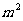 ,墙高为
,墙高为 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元 ,其余三面的造价为200元
,其余三面的造价为200元 ,屋顶的造价为250元
,屋顶的造价为250元 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
解:设地面矩形在门正下方的一边长为 ,则另一边的长为
,则另一边的长为 ,设总造价为
,设总造价为 元,则
元,则
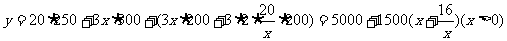 因为
因为  ,当且仅当
,当且仅当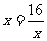 (
( 即
即 时 取“=”,所以,当
时 取“=”,所以,当 时
时 有最小的值
有最小的值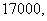 此时
此时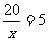 ,
,
答:当储藏室地面矩形在门正下方的一边长为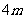 ,另一边的长为
,另一边的长为 时,能使总造价最低造价为17000元。
时,能使总造价最低造价为17000元。
4.一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在 (元)/月收入段应抽出
人
(元)/月收入段应抽出
人
解析:由图知,在 (元)/月收入段应抽出100×
(元)/月收入段应抽出100× =25人
=25人
答案25
3 解答题
3. 两名战士在一次射击比赛中,战士甲得1分、2分、3分的概率分别为0.4、0.1、0.5;战士乙得1分、2分、3分的概率分别为0.1、0.6、0.3,那么两名战士得胜希望大的是
解析:乙 甲获胜的期望与方差分别是:(Eξ)甲=0.4×1+0.1×2+0.5×3=2.1,(Dξ)甲=(2.1-1)2×0.4+(2.1-2)2×0.1+(2.1-3)2×0.5=0.89.
乙获胜的期望与方差分别是:(Eξ)乙=0.1×1+0.6×2+0.3×3=2.2,(Dξ)乙=(2.2-1)2×0.1+(2.2-2)2×0.6+(2.2-3)2×0.3=0.456.
∵乙的期望高于甲,且乙的水平比甲稳定,故得胜希望大的是乙.
答案: 乙

2. 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,则这对双胞胎的作业同时被抽中的概率是 (结果用最简分数表示).
解析: 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,这对双胞胎的作业同时被抽中的概率是

1. 已知A、B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离x表示为时间t(小时)的函数表达式是
答案:
11、设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为 ( )
A.15 B.10 C.20 D.5
解析:因为15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为150×
答案 B
12银行计划将某客户的资金给项目M和N投资一年,其中40%的资金给项目M,60%的资金给项目N,项目M能获得10%的年利润,项目N能获得35%的年利润。年终银行必须回笼资金,同时按一定的回报率支付给客户。为了使银行年利润不小于给M、N总投资的10%而不大于总投资的15%,则给客户的回报率最大值为 ( )
A.5% B.10% C.15% D.20%
解析:设客户投资为a,客户的回报率为x,依题意0.1a≤0.4(1+0.1)a+.06(1+0.35)a-ax≤0.15a,解得0.1≤x≤0.15,选择C。
答案 C
2 填空题
5. 某人从2002年1月1日起,且以后每年1月1日到银行存入a元(一年定期),若年利
率r保持不变,且每年到期后存款均自动转为新一年定期,到2008年1月1日将所有存款及利息全部取回,他可取回的钱数(单位为元)为
?A.a(1+r)7 B.  [(1+r)7-(1+r)]?C.a(1+r)8 D.
[(1+r)7-(1+r)]?C.a(1+r)8 D.  [(1+r)8-(1+r)]
[(1+r)8-(1+r)]
解析:2007年1月1日,2006年1月1日,…,2002年1月1日存入钱的本息分别为:a(1+r),a(1+r)2,…,a(1+r)6.相加即可,选择B
答案B
6停车场划出一排12个停车位置,今有8辆车需要停放,要求空车位连在一起,不同的停车方法有( )
A.A 种
B.A
种
B.A 种
C.A
种
C.A ·C
·C 种 D.A
种 D.A ·C
·C 种
种
解析:插空法.空车位插入8辆车的9个空格,故有C ·A
·A .选择.D?
.选择.D?
答案:D
7某单位有三个科室,为实现减员增效,每科室抽调2人去参加再就业培训,培训后这6人中有2人返回单位,但不回到原科室工作,且每科室至多安排一人,问共有多少种不同的安排方法( )
A.75种 B.42种 C.30种 D.15种
解析:分两类:(1)返回两人来自同一科室,返回有A 种,故有C
种,故有C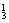 ·A
·A =6;(2)两人来自不同的科室,返回有2+1=3,故有(C
=6;(2)两人来自不同的科室,返回有2+1=3,故有(C C
C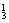 )·3=36种.共有42种. 选择B
)·3=36种.共有42种. 选择B
答案:B
8从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( )
A. 140种 B. 120种 C. 35种 D. 34种
解析: 从反面考虑,7人任意选4人的 方法数减去全选男生的 方法数即为所求
故既有男生又有女生的不同的选法共有 。
。
答案:D
9采用系统抽样的方法,从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的概率是 ( )
A. B.
B.
 C.
C.
 D.
D.
解析:抽样过程中每个个体被抽到的概率是相等的,为
答案C
10抛掷两个骰子,至少有一个4点或5点出现时,就说这些试验成功,则在10次试验中,成功次数ξ的期望是 ( )
A.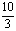 B.
B. C.
C.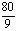 D.
D.
解析:成功次数ξ服从二项分布,每次试验成功的概率为1- =
= ,故在10次试验中,成功次数ξ的期望为
,故在10次试验中,成功次数ξ的期望为 ×10=
×10=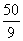
答案 D
4. .设导弹发射的事故率为0.01,若发射导弹10次,其中出事故的次数为ξ,则下列结论正确的是( )
A.Eξ=0.1 B.P(ξ=k)=0.01k·0.9910-k C.Dξ=0.1 D.P(ξ=k)=C 0.99k·0.0110-k
0.99k·0.0110-k
解析:∵P(ξ=k)=C ·0.01k(1-0.01)10-k,Eξ=nP=0.1.选择A
·0.01k(1-0.01)10-k,Eξ=nP=0.1.选择A
答案 A
3. 一个人以6米/秒的速度去追停在交通灯前的汽车,当他离汽车25米时,交通灯由红变绿,汽车以1米/秒的加速度匀加速开走,那么 ( )
A.人可在7秒内追上汽车 B.人可在10秒内追上汽车
C.人追不上汽车,其间距离最近为5米 D.人追不上汽车,其间距离最近为7米
解析:本题是一道加速行程问题,需要运用物理知识建立数学模型,即通过加速运动建立二次函数关系式.若经t秒人刚好追上汽车,则S+25=6t,由S=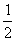 t2,得
t2,得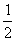 t2-6t+25=0
t2-6t+25=0 t2-12t+50=0.考虑距离差d=(S+25)-6t=
t2-12t+50=0.考虑距离差d=(S+25)-6t=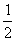 t2-6t+25=
t2-6t+25=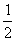 (t-6)2+7,故当t=6秒时,d有最小值7米,即人与汽车最少相距7米,故选D.
(t-6)2+7,故当t=6秒时,d有最小值7米,即人与汽车最少相距7米,故选D.
答案 D
D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com