
题目列表(包括答案和解析)
6.某一批袋装大米质量服从正态分布N(10,0.01)(单位:kg),任选一袋大米,它的质量在9.8kg-10.2kg内的概率是
A、1- (2)
B、2
(2)
B、2 (2)-1 C、F(2)-F(-2) D、F(2)+F(-2)-1
(2)-1 C、F(2)-F(-2) D、F(2)+F(-2)-1
4. 函数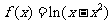 的单调递增区间为
的单调递增区间为
A、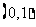 B、
B、 C、
C、 D、
D、
5.下面给出四个命题:
① 直线 与平面
与平面 内两直线都垂直,则
内两直线都垂直,则 。②经过直线
。②经过直线 有且仅有一个平面垂直于直线
有且仅有一个平面垂直于直线 ③过平面
③过平面 外两点,有且只有一个平面与
外两点,有且只有一个平面与 垂直。④直线
垂直。④直线 同时垂直于平面
同时垂直于平面 、
、 ,则
,则 ∥
∥ 。其中正确的命题个数为
。其中正确的命题个数为
A、0 B、1 C、2 D、3
3. 二项式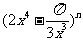 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数 的最小值为
的最小值为
A、7 B、12 C、14 D、5
2. 在等差数列 中,
中, =9,
=9, =3,则
=3,则 =
=
A、0 B、3 C、6 D、-3
1. 复数 满足方程:
满足方程: ,则
,则 =
=
A、 B、
B、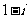 C、
C、
 D、
D、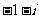
22.(理科)在数列 (n
(n )中,当n为奇数时,
)中,当n为奇数时,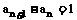 ,当n为偶数时,
,当n为偶数时, ,且
,且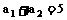 .
.
(1)求 ,
, .
.
(2)令 ,(n
,(n ,判断数列
,判断数列 是否为等差数列,并证明你的结论。求数列
是否为等差数列,并证明你的结论。求数列 的通项公式.
的通项公式.
(3)若对任意给定的正整数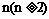 ,数列
,数列 满足
满足
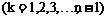 ,
, ,求
,求 .
.
21. (理科)设集合P=
(理科)设集合P=
(1)试判断 ;
;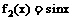 ,是否属于集合P?
,是否属于集合P?
(2)若
 属于P,试寻找其充要条件.
属于P,试寻找其充要条件.
(3)根据对第(1),(2)小题的研究,请你对属于集合P的函数从函数性质方面提出一个有价值的结论,说明理由;若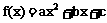
 ,利用研究所得的结论判断
,利用研究所得的结论判断 与集合P的关系.
与集合P的关系.
20. 设A,B分别是双曲线
设A,B分别是双曲线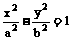
 的左右顶点,双曲线的实轴长为
的左右顶点,双曲线的实轴长为 ,焦点到渐近线的距离为
,焦点到渐近线的距离为 .
.
(1)求此双曲线的方程.
(2)已知直线 与双曲线的右支交于
与双曲线的右支交于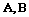 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点 ,使得
,使得 ,求
,求 的值及点
的值及点 的坐标.
的坐标.
19.一长方形泳池中相邻的两条泳道 和
和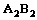 (看成两条互相平行的线段)分别长90米,甲在泳道
(看成两条互相平行的线段)分别长90米,甲在泳道 上从
上从 处出发,以3米/秒的速度到达
处出发,以3米/秒的速度到达 以同样的速度返回
以同样的速度返回 处,然后重复上述过程;乙在泳道
处,然后重复上述过程;乙在泳道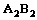 上从
上从 处出发,以2米/秒的速度到达
处出发,以2米/秒的速度到达 以同样的速度游回
以同样的速度游回 处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
 (1)设甲离开池边
(1)设甲离开池边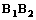 处的距离为y米,当时间
处的距离为y米,当时间 (单位:
(单位:
秒)时,写出y关于t的函数解析式.
(2)在右图的直角坐标系中,x轴表示时间 (单位:秒),
(单位:秒),
y轴表示离开池边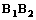 处的距离.在同一个坐标系中画出
处的距离.在同一个坐标系中画出
甲乙两人各自运动的函数图像.(实线表示甲的图像,虚线表示乙的图像).
 (3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.
(3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.


18.已知函数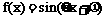 (其中
(其中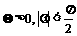 ),
), .若函数
.若函数 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为 ,且直线
,且直线 是函数
是函数 图像的一条对称轴.
图像的一条对称轴.
(1)求 的表达式.
的表达式.
(2)求函数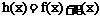 的单调递增区间.
的单调递增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com