
题目列表(包括答案和解析)
5、方程 有实根的概率为( ).
有实根的概率为( ).
A、 B、
B、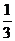 C、
C、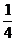 D、
D、
4、若曲线 的一条切线
的一条切线 与直线
与直线
垂直,则切线 的方程为( ).
的方程为( ).
A、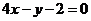 B、
B、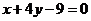
C、 D、
D、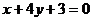
3、如果执行的程序框图(右图所示),那么输出的 ( ).
( ).
A.2450 B.2500 C.2550 D.2652
2、已知椭圆的长轴长是短轴长的 倍,则椭圆的离心率等于( ).
倍,则椭圆的离心率等于( ).
A.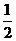 B.
B.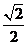 C.
C. D.
D.
1、设函数 的定义域为集合M,集合N=
的定义域为集合M,集合N= ,则
,则 ( ).
( ).
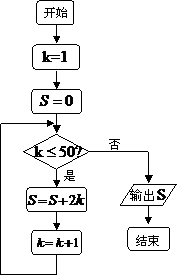 A.
A. B.N C.
B.N C. D.M
D.M
21、(本小题满分14分)设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程
 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 ”.
”.
(Ⅰ)判断函数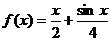 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(Ⅱ)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n] D,都存在
D,都存在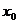
 [m,n],使得等式
[m,n],使得等式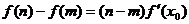 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程 只有一个实数根;
只有一个实数根;
(Ⅲ)设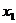 是方程
是方程 的实数根,求证:对于
的实数根,求证:对于 定义域中任意的
定义域中任意的 ,当
,当 ,且
,且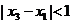 时,
时,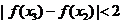 .
.
20、 (本小题满分14分)给定圆P:
(本小题满分14分)给定圆P: 及抛物
及抛物
线S: ,过圆心
,过圆心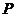 作直线
作直线 ,此直线与上述两曲线
,此直线与上述两曲线
的四个交点,自上而下顺次记为 ,如果线
,如果线
段 的长按此顺序构成一个等差数列,求直
的长按此顺序构成一个等差数列,求直
线 的方程.
的方程.
19、 (本小题满分14分)如图,已知四棱锥
(本小题满分14分)如图,已知四棱锥 的
的
底面 是菱形;
是菱形; 平面
平面 ,
, ,
,
点 为
为 的中点.
的中点.
(Ⅰ)求证: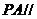 平面
平面 ;
;
(Ⅱ)求二面角 的正切值.
的正切值.
18、(本小题满分14分)一个口袋中装有大小相同的2个白球和4个黑球.
(Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
(方差: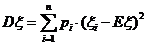 )
)
17、(本小题满分12分)设函数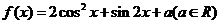 .
.
(Ⅰ)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当 时,
时, 的最大值为2,求
的最大值为2,求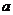 的值,并求出
的值,并求出 的对称轴方程.
的对称轴方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com