22.设二次函数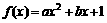 (a>0且b≠0).

(1)已知|f (0)|=|f (1)|＝|f (-1)|=1，求f(x)的解析式和f(x)的最小值.

(2)已知f (x)的对称轴方程是x=1，当f (x)的图象在x轴上截得的弦长不小于2时，试求a、b、c满足的条件.

(3)已知|b|≤a，|f (0)|≤1，|f (1)|≤1，|f (-1)|≤1.证明：当|x|≤1时，|f (x)|≤.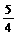

21.已知二次函数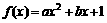(a、b∈R,a>0),设方程f (x)=x的两个实数根为和.

(1)如果<2<<4,设函数f (x)的对称轴为x=,求证：>-1;

(2)如果||<2,|-|=2,求b的取值范围.

20.西部某地区因交通问题严重制约经济发展，某种土特产品只能在本地销售，每年投资x万元，所获利润为p=-(万元).在实施西部大开发战略中，该地区在制订经济发展十年规划时，拟开发此种土特产品.开发前后，财政预算每年均可投入专项资金60万元，要开发此产品，需先用5年时间修通公路，所需资金从60万元的预算资金中每年拿出30万元.公路修通后该土特产品在异地销售，每投资x万元，可获利润：q=-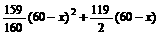(万元). 问从10年的总利润

来看，该项目有无开发价值?

19.已知函数f (x)=(a>0，x>0).

(1)求证：f (x)在(0，+∞)上是递增函数.

(2)若f (x)在［m,n］上的值域是［m,n］(m≠n)，求a的取值范围并求相应的m、n的值.

(3)若f (x)≤2x在(0，+∞)上恒成立，求a的取值范围.

18.对于映射f (x)＝，有适合f (x)＝x的x时，这个x叫做f (x)的不动点.

(1)求使f (x)有绝对值相等且符号相反的两个不动点时a、b所满足的条件.

(2)在(1)的条件下，当a=3时，f (x)的两个不动点对应于函数y=f (x)图象上的两个点，记为A、B，C为函数y=f (x)图象上另一点，且>2，求点C到直线AB距离的最小值及取得最小值时对应的C点的坐标.

17.已知函数f (x)=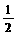lg(kx),g(x)=lg(x+1).

(1)求f (x)-g(x)的定义域；

(2)若方程f (x)=g (x)有且仅有一个实根，求实数k的取值范围.

16.设函数f(x)的反函数为h(x)，函数g(x)的反函数为h(x+1)，已知f (2)=5,f (5)=-2，f (-2)=8，那么g(2)、g(5)、g(8)、g(-2)中，一定能求出具体数值的是　　　　　 .

15.记号［x］表示不超过4的最大整数，则y＝［x］的图象与直线y＝x-1的图象的交点个数是　　　　　 .

14.f (x)与g(x)分别是一个奇函数和一个偶函数，若f (x)-g(x)=,则f (-1)、g(0)、g(-2)从小到大的顺序是　　　　　 .

13.若f (x)=|x-2a|+x-1函数值恒为正,则a的取值范围是　　　　　 .