
题目列表(包括答案和解析)
3.若点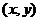 在椭圆
在椭圆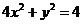 上,则
上,则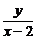 的最小值为
( )
的最小值为
( )
A.1 B.-1 C.-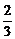
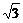 D.以上都不对
D.以上都不对
2.到两定点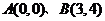 距离之和为
距离之和为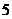 的点的轨迹是
( )
的点的轨迹是
( )
A.椭圆 B.AB所在直线 C.线段AB D.无轨迹
1.设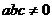 ,“
,“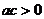 ”是“曲线
”是“曲线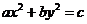 为椭圆”的
( )
为椭圆”的
( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
6.
⑴ 解:设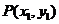 ,
, ,因为双曲线的离心率为
,因为双曲线的离心率为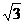 ,
,
所以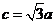 ,
,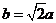 ,双曲线方程为
,双曲线方程为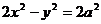 ,
,
因为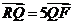 ,所以
,所以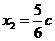 ,
,
因为直线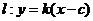 ,所以
,所以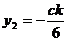 ,
,
点Q是双曲线上一点,所以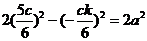 ,
,
整理得,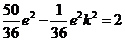 ,解得
,解得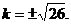
⑵ 证明:设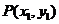 ,
,
由已知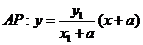 ,
,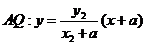 ,
,
所以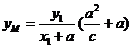 ,
,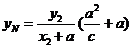 ,
,
所以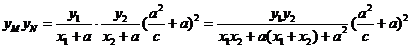 ,
,
由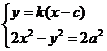 ,得
,得
所以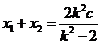 ,
,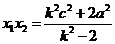 ,
,
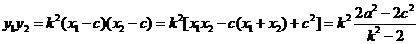
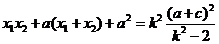
所以,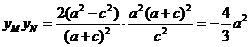
5.
⑴ 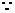
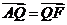
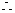
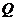 为AF的中点.
为AF的中点.
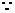

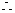
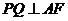
 是
是 的垂直平分线
的垂直平分线 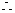
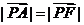
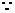
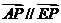
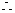 A、E、P三点共线
A、E、P三点共线
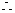 P为AF的垂直平分线与AE的交点
P为AF的垂直平分线与AE的交点
∴ 点P的轨迹为椭圆,且 ,
,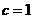
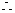
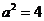 ,
,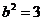
∴ 所求的椭圆方程为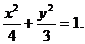
⑵ 设两交点的坐标为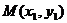 、
、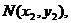 则
则
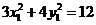 ,
,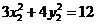
由已知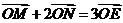 可得:
可得:
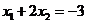 ,
,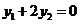
由上式可组成方程组为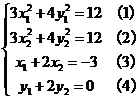
把⑶、⑷代入⑴得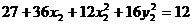 ⑸
⑸
⑸ - ⑵×4得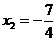 ,把
,把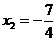 代入⑵得
代入⑵得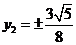
直线MN与x轴显然不垂直,
∴ 所求直线MN的斜率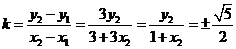
∴ 所求的直线MN的方程为
4.
⑴ 椭圆的右顶点为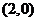 (2,0),
(2,0),
设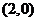 关于直线
关于直线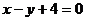 的对称点为
的对称点为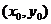 ,
,
则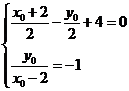 ,解得
,解得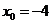 ,
,
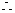
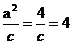 ,
,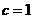
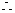
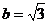 ,所求椭圆方程为
,所求椭圆方程为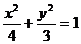
⑵ 设A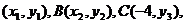
由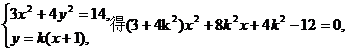
所以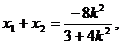 ………① ,
………① ,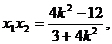 ………②
………②
因为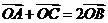 ,即
,即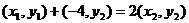 ,
,
所以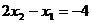 ……③
……③
由①③得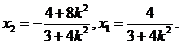
代入②得, ,整理得
,整理得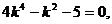
所以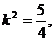 所以
所以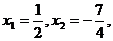
由于对称性,只需求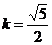 时,△OAB的面积.
时,△OAB的面积.
此时,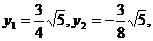 所以
所以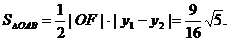
3.
⑴ 设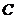 、
、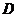 点的坐标分别为
点的坐标分别为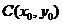 ,
,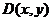 ,则:
,则:
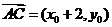 ,
,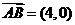 ,
,
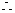

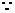
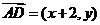
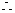
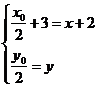 ,解得
,解得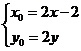
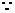
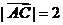 ,即
,即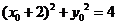
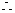
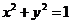 ,即为点
,即为点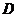 的轨迹方程
的轨迹方程
⑵ 易知直线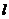 与
与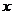 轴不垂直,设直线
轴不垂直,设直线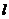 的方程为
的方程为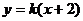 ①.
①.
又设椭圆方程为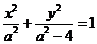
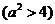 ②.
②.
因为直线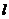 与圆
与圆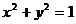 相切,故
相切,故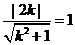 ,解得
,解得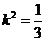
将①代入②整理得,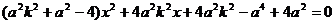 ,
,
而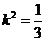 ,即
,即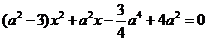 ,
,
设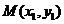 ,
,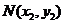 ,则
,则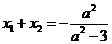 ,
,
由题意有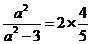
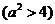 ,求得
,求得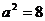 ,经检验,此时
,经检验,此时
故所求的椭圆方程为
2.
⑴  ……2分
……2分
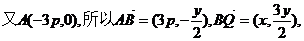
由已知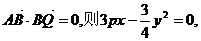 ……………………4分
……………………4分
 …………5分
…………5分
⑵ 设过点A的直线为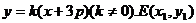 、F(x2,y2)
、F(x2,y2)
联立方程组 ……7分
……7分
y1y2=12p2………………8分
 …………10分
…………10分
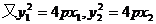 , 所以
, 所以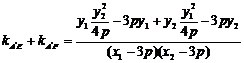
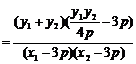 …………………………13分
…………………………13分
由y1y2=12p2,得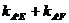 =0…………14分
=0…………14分
1.
⑴由已知,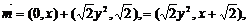
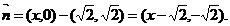
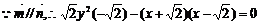
即所求曲线的方程是: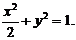
⑵由(I)求得点M(0,1),显然直线l与x轴不垂直,
故可设直线l的方程为y=kx+1.
由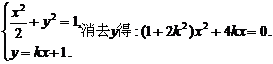
解得x1=0, x2=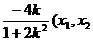 分别为M,N的横坐标).
分别为M,N的横坐标).
由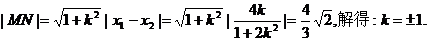
所以直线l的方程x-y+1=0或x+y-1=0.
6.
双曲线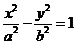
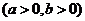 的离心率为
的离心率为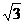 ,
,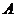 、
、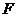 分别是双曲线的左顶点、右焦点,过点
分别是双曲线的左顶点、右焦点,过点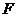 的直线
的直线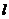 交双曲线的右支于
交双曲线的右支于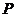 、
、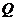 两点,交
两点,交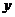 轴于
轴于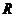 点,
点,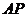 、
、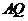 分别交右准线于
分别交右准线于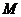 、
、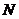 两点.
两点.
⑴ 若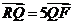 ,求直线
,求直线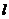 的斜率;
的斜率;
⑵ 证明: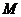 、
、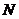 两点的纵坐标之积为
两点的纵坐标之积为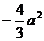 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com