
题目列表(包括答案和解析)
6. 向量的加法法则
(1)三角形法则:(首尾连接)
(2)平行四边形法则:(共起点)
5. 向量的加法:
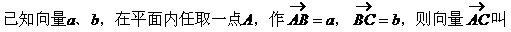
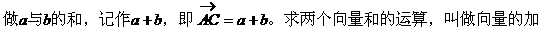 法。
法。
注意:(1)两个向量的和仍为向量。
(2)对于零向量与任一向量a有a+0=0+a=a。
4. 平行向量、相等向量、共线向量。
平行向量(共线向量):方向相同或相反的非零向量叫做平行向量。规定0与任一向量平行,平行向量也叫做共线向量。
相等向量:长度相等且方向相同的向量叫做相等向量。任意两个相等的非零向量都可以用同一条有向线段表示。
3. 零向量与单位向量:
零向量:长度为零的向量叫做零向量,记作0。
单位向量:长度等于1个单位长度的向量叫做单位向量。
2. 向量的表示方法:
(1)几何表示法。向量可以用有向线段表示,如:A→B

1. 向量的概念:向量是既有大小,又有方向的量。向量的大小(长度)叫做向量的模,模是非负数,可以比较大小,但由于方向不能比较大小,所以,向量不可以比较大小,这是数量与向量的最大差异。
向量及其运算习题课
19. 已知 的图象F按
的图象F按 平移得到
平移得到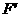 的图象,已知点
的图象,已知点 在
在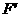 上,F与
上,F与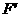 的交点是
的交点是 ,试求F的解析式。
,试求F的解析式。
18. 已知四边形ABCD是梯形,其中 ,A、B、C三点的坐标依次为
,A、B、C三点的坐标依次为 ,
,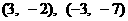 ,且
,且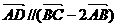 ,求D点坐标。
,求D点坐标。
17. 在 ABCD中,已知
在 ABCD中,已知 ,AE与DB交于F点。设
,AE与DB交于F点。设 ,用a表示
,用a表示 、
、 的值。
的值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com