
题目列表(包括答案和解析)
7. 若 三点共线,则( )
三点共线,则( )
A. 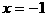 B.
B.

C.  D.
D.

6. 在四边形ABCD中, ,
,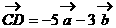 ,其中
,其中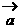 、
、 不共线,则四边形ABCD为( )
不共线,则四边形ABCD为( )
A. 平行四边形 B. 矩形 C. 梯形 D. 菱形
5. 若 ,则向量
,则向量 =( )
=( )
A.  B.
B.  C.
C.  D.
D. 
4. 化简 的结果是( )
的结果是( )
A.  B.
B.  C.
C. 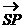 D.
D. 
3.  为非零向量,且
为非零向量,且 ,则( )
,则( )
A.  方向相同
方向相同
B. 
C. 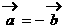
D. 以上都不对
2. 向量
A. 充分不必要条件
B. 必要非充分条件
C. 充要条件
D. 非充分也非必要条件
1. 下列说法中正确的是( )
A. 两个长度相等的向量一定相等,
B. 相等的向量起点必相同
C. 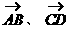 共线,则A、B、C、D四点必在同一直线上
共线,则A、B、C、D四点必在同一直线上
D. 相等的向量一定是平行向量
33. 在平移向量a及平移前后函数图象的解析式y=f(x),y=g(x)三者之中,知道了两个能求出第三个。
[例题选讲]
例1. 设a、b是非零向量,且a与b不平行,求证a+b与a-b不平行。
分析:如果结论不成立,即(a+b)//(a-b),将会得到什么样的结果呢?因为两个向量共线,必定存在一个实数λ,使一个向量的λ倍恰好等于另一个向量。由此得到的关于a、b的等式就能推出与题设矛盾。
解: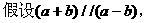

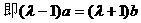
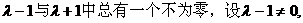

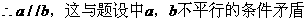

小结:命题由否定形式出现,通常可考虑用反证法来证明。因为本题难度不大,所以也可直接利用向量平行的充要条件验证。如,
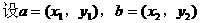

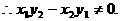



例2. 

分析:(1)注意c2=|c|2,根据向量数量积的定义及运算律先求出c2;

解:




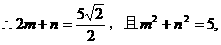

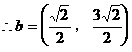
小结:第(2)题把题中的向量a的起点设为原点,在图中旋转容易理解,但实际上与起点的位置无关。解题的思路能推广到一般情况。另外,结合图形可知n>1,从而在二元二次方程组的解中选取适合题意的解。
例3. 

分析: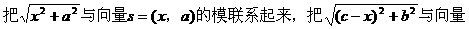

解:


小结:直接用代数的方法求本题中的函数最值很困难,一般情况下转化为几何模型求解。这里借助向量计算,本质上还是几何模型,但运算简捷了。
例4. 如图所示,P、Q是△ABC的边BC上两点,且BP=QC。
求证: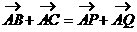

证明:

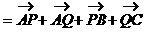
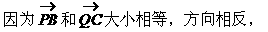
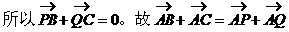
小结:


例5. 

解:
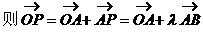
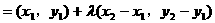



小结:

例6. 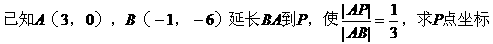
解法一:


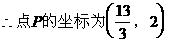
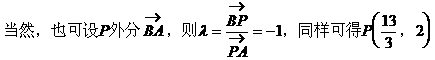
解法二:




小结:在采用定比分点公式解题时,起点、终点、分点及相应的比值λ都是相对的,它们的位置关系可以根据问题的特点作适当调整。
例7. 

解法一:

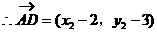
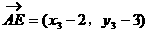




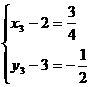
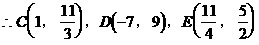
解法二:
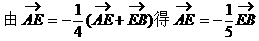

由定比分点公式,可得:





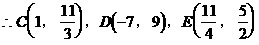
小结:本题是向量坐标表示的典型题,方法一主要是运用若向量相等,则其坐标相等这一原则来解,思路清晰,易于理解,方法二主要运用定比分点公式求点的坐标,此题关 形式,从而分别求出λ。
形式,从而分别求出λ。
例8. 
 解:
解:
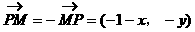

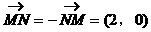

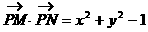





小结:本例为2002年高考题(21)题第(1)小题,主要考查向量的数量积的坐标表示及等差数列基础知识等。
例9. 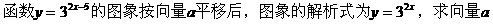
解法一:

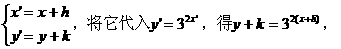



解法二:





小结:从本例可以看出,如果把函数图像的解析式从一种形式变为另一种形式有两种方法,这两种方法实质相同,都应对此深刻理解。
[模拟试题]
28. 数量积的重要性质
设a,b均为非零向量,e是与b方向相同的单位向量,θ是a与e的夹角(则a与b的夹角也为θ),由数量积的定义可得如下五条重要性质:
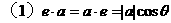
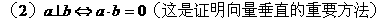



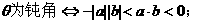

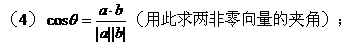


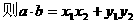




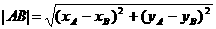
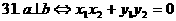

27. a·b的几何意义
数量积a·b等于a的长度|a|与b在a方向上的投影|b|cosθ的乘积,也等于b的长度|b|与a在b方向上的投影|a|cosθ的乘积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com