4．已知数列{a_n}，如果a₁,a₂-a₁，a₃-a₂，…，a_n-a_n-1，…是首项为1，公比为的等比数列，则a_n等于(n∈N)　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.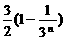　　　　　　 B.　　　 C.　　　　 D.

3．若正数a、b、c依次成公比大于1的等比数列，则当x>1时，log_ax、log_bx、log_cx(　　 )

A.依次成等差数列　　　　　　　 B.依次成等比数列

C.各项的倒数依次成等差数列　　 D.各项的倒数依次成等比数列

2．从{1,2,3,4,5,6,7,8,9,10}中任选3个不同的数使它们成等差数列，则这样的等差数列最多有　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　(　　 )

A.20个　　　　 B.40个　　　　 C.60个　　　　 D.80个

1．下列各命题中，真命题是　　　　　　　　　　　　　　　　　　 　　　　　　(　　 )

A．若{a_n}成等差数列，则{|a_n|}也成等差数列

B．若{|a_n|}成等差数列，则{a_n}也成等差数列

C．若存在自然数n,使得2a_n+1=a_n+a_n+2，则{a_n}一定是等差数列

D．若{a_n}是等差数列，对任何自然数n都有2a_n+1=a_n+a_n+2

17．对任意函数f(x),x∈D，可按图所示构造一个数列发生器，其工作原理如下：

①输入数据x₀∈D，经数列发生器输出x₁=f(x₀)；

②若x₁D，则数列发生器结束工作；若x₁∈D，则将x₁反馈回输入端，

再输出x₂=f(x₁)，并依此规律继续下去．现定义f(x)=.

(1)若输入x₀=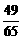，则由数列发生器产生数列{x_n}，请写出数列{x_n}

的所有项(n∈N)；

　 (2)若要数列发生器产生一个无穷的常数数列，试求输入的初始数据

x₀的值；

(3)若输入x₀时，产生的无穷数列{x_n}满足：对任意正整数n，均有x_n<x_n+1，求x₀的取值范围．

16．某工厂年度初借款A元，从该年度末开始，每年偿还一定金额x元，恰在n年内还清(包括借款的利息)，借款的年利率为r，求每年偿还的金额.

15．数列{a_n}的前n项和记为S_n,已知a₁=1,a_n+1=S_n(n=1,2,3,…).证明：

(1)数列{}是等比数列;

(2)S_n+1=4an.

14．已知一个项数为偶数，首项为1的等比数列，其奇数项的和为85，偶数项的和为170，求这个等比数列的公比q及项数n.

13．在和n+1之间插入n个正数，使这n+2个数依次成等比数列，求所插入的n个数之积.

12．设函数f(x)=log₂x-log_x2(0<x<1),数列{a_n}满足f(2^an)=2n(n∈N).

(1)求数列{a_n}的通项公式;

(2)判定数列的单调性.