
题目列表(包括答案和解析)
2.(辽宁6)设P为曲线C: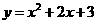 上的点,且曲线C在点P处切线倾斜角的取值范围为
上的点,且曲线C在点P处切线倾斜角的取值范围为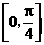 ,则点P横坐标的取值范围为( A
)
,则点P横坐标的取值范围为( A
)
A. B.
B.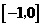 C.
C.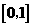 D.
D.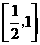
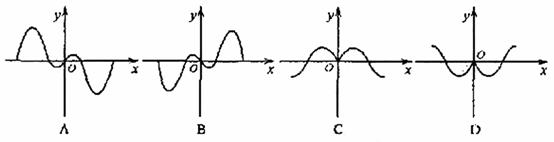
1.(福建11)如果函数y=f(x)的图象如右图,那么
导函数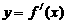 的图象可能是( A )
的图象可能是( A )

33. (重庆文)(18)(本小题满分13分,(1)小问8分,(2)小问5分.)
在每道单项选择题给出的4个备选答案中,只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案,求这4道题中:
(1)恰有两道题答对的概率;
(2)至少答对一道题的概率.
解:视“选择每道题的答案”为一次试验,则这是4次独立重复试验,且每次试验中“选择正确”这一事件发生的概率为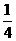 .
.
由独立重复试验的概率计算公式得:
(1)恰有两道题答对的概率为
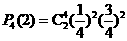

(2)解法一:至少有一道题答对的概率为
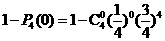

解法二:至少有一道题答对的概率为
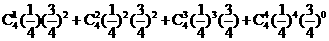

32.(重庆理)(18)(本小题满分13分,(1)小问5分,(2)小问8分.)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为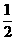 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1) 打满3局比赛还未停止的概率;
(2)比赛停止时已打局数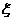 的分别列与期望E
的分别列与期望E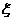 .
.
解:令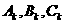 分别表示甲、乙、丙在第k局中获胜.
分别表示甲、乙、丙在第k局中获胜.
(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比
赛还未停止的概率为

(2)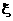 的所有可能值为2,3,4,5,6,且
的所有可能值为2,3,4,5,6,且
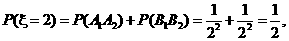
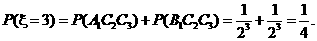
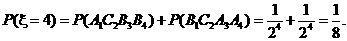

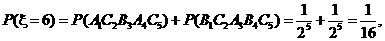
故有分布列
 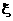 |
2 |
3 |
4 |
5 |
6 |
|
P |
 |
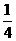 |
 |
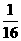 |
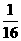 |
从而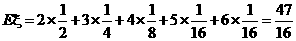 (局).
(局).
31.(浙江文)(19)(本小题满分14分)一个袋中装有大小相同的黑球、白球和红球。已知袋中共有10个球。从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是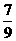 。求:
。求:
(1)从中任意摸出2个球,得到的都是黑球的概率;
(2)袋中白球的个数。
解:(1)由题意知,袋中黑球的个数为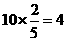 .
.
记“从袋中任意摸出两个球,得到的都是黑球”为事件A,则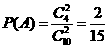 .
.
(2)记“从袋中任意摸出两个球,至少得到一个白球”为事件B,
设袋中白球的个数为 ,则
,则
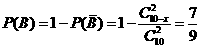 ,得到
,得到 .
.
30.(浙江理)(19).(本题14分)一个袋中装有若干个大小相同的黑球,白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是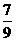 .
.
(1)若袋中共有10个球,(ⅰ)求白球的个数;(ⅱ)从袋中任意摸出3个球,记得到白球的个数为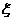 ,求随机变量
,求随机变量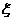 的数学期望
的数学期望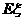 .
.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于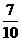 .并指出袋中哪种颜色的球个数最少.
.并指出袋中哪种颜色的球个数最少.
(1)解:(i)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,设袋中白球的个数为 ,则
,则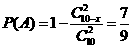 ,得到
,得到 .故白球有5个.
.故白球有5个.
(ii)随机变量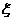 的取值为0,1,2,3,分布列是
的取值为0,1,2,3,分布列是
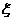 |
0 |
1 |
2 |
3 |
 |
 |
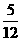 |
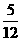 |
 |
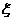 的数学期望
的数学期望
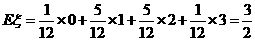 .
.
(2)证明:设袋中有 个球,其中
个球,其中 个黑球,由题意得
个黑球,由题意得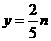 ,
,
所以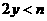 ,
, ,故
,故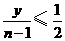 .
.
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则

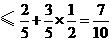 .
.
所以白球的个数比黑球多,白球个数多于 ,红球的个数少于
,红球的个数少于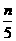 .
.
故袋中红球个数最少.
29.(天津文)18.(本小题满分12分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与
与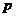 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为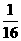 .
.
(1)求乙投球的命中率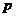 ;
;
(2)求甲投球2次,至少命中1次的概率;
(3)若甲、乙两人各投球2次,求两人共命中2次的概率.
(1)解法一:设“甲投球一次命中”为事件 ,“乙投球一次命中”为事件
,“乙投球一次命中”为事件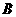 ,由题意得
,由题意得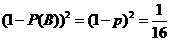 ,
,
解得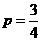 或
或 (舍去),所以乙投球的命中率为
(舍去),所以乙投球的命中率为 .
.
解法二:设“甲投球一次命中”为事件 ,“乙投球一次命中”为事件
,“乙投球一次命中”为事件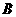 ,由题意得
,由题意得
 ,
,
于是 或
或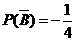 (舍去),故
(舍去),故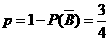 .
.
所以乙投球的命中率为 .
.
(2)解法一:由题设和(Ⅰ)知,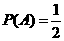 ,
,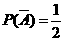 .
.
故甲投球2次至少命中1次的概率为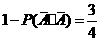 .
.
解法二:由题设和(1)知,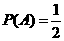 ,
,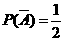 .
.
故甲投球2次至少命中1次的概率为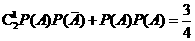 .
.
(3)解:由题设和(1)知,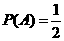 ,
,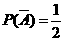 ,
,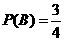 ,
, .
.
甲、乙两人各投球2次,共命中2次有三种情况:甲、乙两人各中一次;甲中2次,乙2次均不中;甲2次均不中,乙中2次.概率分别为
 ,
,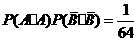 ,
, .
.
所以甲、乙两人各投球2次,共命中2次的概率为 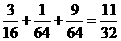 .
.
28.(天津理)18.(本小题满分12分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与
与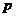 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为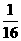 .
.
(1)求乙投球的命中率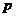 ;
;
(2)若甲投球1次,乙投球2次,两人共命中的次数记为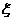 ,求
,求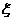 的分布列和数学期望.
的分布列和数学期望.
解:(1)设“甲投球一次命中”为事件 ,“乙投球一次命中”为事件
,“乙投球一次命中”为事件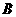 ,
,
由题意得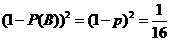 ,
,
解得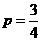 或
或 (舍去),所以乙投球的命中率为
(舍去),所以乙投球的命中率为 .
.
(2)由题设和(Ⅰ)知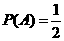 ,
,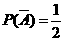 ,
,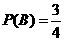 ,
, .
.
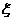 可能的取值为0,1,2,3,故
可能的取值为0,1,2,3,故
 ,
,
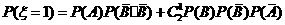
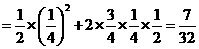 ,
,
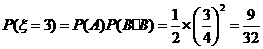 ,
,
 .
.
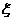 的分布列为
的分布列为
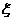





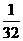
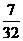

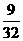
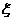 的数学期望
的数学期望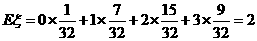 .
.
27.(四川文)(18).(本小题满分12分)设进入某商场的每一位顾客购买甲商品的概率为0.5,购买乙商品的概率为0.6,且顾客购买甲商品与购买乙商品相互独立,各顾客之间购买商品是相互独立的.
(1)求进入该商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入该商场的3位顾客中,至少有2位顾客既未购买甲种也未购买乙种商品的概率;
解:(1)记A表示事件:进入该商场的1位顾客选购甲种商品.
B表示事件:进入该商场的1位顾客选购乙种商品.
C表示事件:进入该商场的1位顾客选购甲、乙两种商品中的一种.
则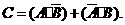
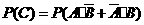 =
=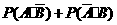 =
=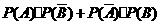
=0.5×0.4+0.5×0.6=0.5.
(2)记A2表示事件:进入该商场的3位顾客中恰有2位顾客既未选购甲种商品,也未选购乙种商品.
A2表示事件:进入该商场的3位顾客中都未选购甲种商品,也未选购乙种商品.
D表示事件:进入该商场的1位顾客未选购甲种商品,也未选购乙种商品.
E表示事件:进入该商场的3位顾客中至少有2位顾客既未选购甲种商品,也未选购乙种商品.
则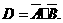
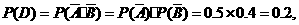

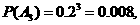
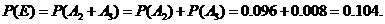
26.(四川理)(18).(本小题满分12分) 设进入某商场的每一位顾客购买甲种商品的概率为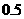 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记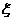 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求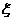 的分布列及期望。
的分布列及期望。
解:记 表示事件:进入商场的1位顾客购买甲种商品,
表示事件:进入商场的1位顾客购买甲种商品,
记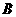 表示事件:进入商场的1位顾客购买乙种商品,
表示事件:进入商场的1位顾客购买乙种商品,
记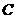 表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
记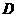 表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
(1)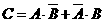

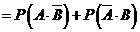

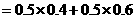

(2)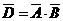 ,
,
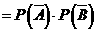
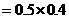
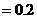
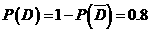
(3) ,故
,故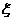 的分布列
的分布列
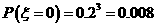 ,
,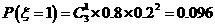
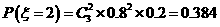 ,
,
所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com