
题目列表(包括答案和解析)
2.某中学高一年级有学生1200人,高二年级有学生900人,高三年级有学生1500人,现用分层抽样的方法从中抽取一个容量为720的样本进行某项调查,则高二年级应抽取的学生数为( )
A.180 B.240 C.480 D.720
1.设复数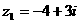 ,
, ,则复数
,则复数 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(17)(本小题满分12分)
在△ABC中,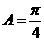 ,
, .
.
(Ⅰ)求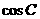 ;
;
(Ⅱ)设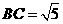 ,求
,求 .
.
(18)(本小题满分12分)
在4名男生和3名女生中挑选3人参加志愿者服务活动,
(Ⅰ)求至多选中1名女生的概率;
(Ⅱ)记女生被选中的人数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(19)(本小题满分12分)
 如图,正四棱锥P
如图,正四棱锥P ABCD的底面边长与侧棱长都是2,点O为底面ABCD的中心,M为PC的中点.
ABCD的底面边长与侧棱长都是2,点O为底面ABCD的中心,M为PC的中点.
(Ⅰ)求异面直线BM和AD所成角的大小;
(Ⅱ)求二面角M PB
PB D的余弦值.
D的余弦值.
(20)(本小题满分12分)
已知等差数列 的前三项为
的前三项为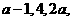 记前
记前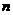 项和为
项和为 .
.
(Ⅰ)设 ,求
,求 和
和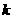 的值;
的值;
(Ⅱ)设 ,求
,求 的值.
的值.
(21)(本小题满分14分)
设A、B分别为椭圆 的左、右顶点,(
的左、右顶点,( )为椭圆上一点,椭圆的长半轴的长等于焦距.
)为椭圆上一点,椭圆的长半轴的长等于焦距.
(Ⅰ)求椭圆的方程;
(Ⅱ)设 ,若直线AP,BP分别与椭圆相交于异于A、B的点M、N,证明在以MN为直径的圆内.
,若直线AP,BP分别与椭圆相交于异于A、B的点M、N,证明在以MN为直径的圆内.
(22)(本小题满分14分)
已知函数
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设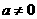 ,函数
,函数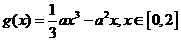 .若对任意
.若对任意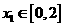 ,总存在
,总存在 ,使
,使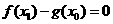 ,求实数
,求实数 的取值范围.
的取值范围.

(11)某校有教师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取-个容量为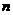 的样本,已知从女生中抽取的人数为80,则
的样本,已知从女生中抽取的人数为80,则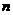 等于
·
等于
·
(12)在如右图所示的程序框图中,当程序被执行后,输出 的结果是 ___
的结果是 ___
(13)在 的展开式中,
的展开式中, 的系数是
(用数字作答).
的系数是
(用数字作答).
(14)已知△ABC的三边长分别为AB=7,BC=5,CA=6,则 的值为
·
的值为
·
(15)有5名男生和3名女生,从中选出5人分别担任语文、数学、英语、物理、化学学科的科代表,若某女生必须担任语文科代表,则不同的选法共有 种(用数字作答).
 (16)如图,圆O是△ABC的外接圆,过点C作圆O的切线,交AB的延长线于点D.若
(16)如图,圆O是△ABC的外接圆,过点C作圆O的切线,交AB的延长线于点D.若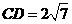 ,AB=BC=3,则BD的长为
;AC的长为
.
,AB=BC=3,则BD的长为
;AC的长为
.
(1)复数 等于
等于
(A)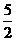 (B)
(B) (C)
(C) (D)
(D)
(2)设变量 满足约束条件
满足约束条件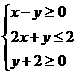 ,则目标函数
,则目标函数 的最小值为
的最小值为
(A) (B)
(B) (C)
(C) (D)
(D)
(3)设集合 ,则
,则
(A)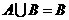 (B)
(B)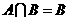
(C) (D)
(D)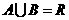
(4)在等比数列 中,
中,
 ,则
,则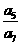 等于
等于
(A) (B)
(B)
(C)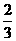 (D)
(D)
(5)过点(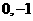 )作直线
)作直线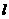 与圆
与圆 交于A、B两点,如果
交于A、B两点,如果 ,则直线
,则直线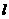 的方程为
的方程为
(A)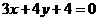 (B)
(B)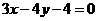
(C)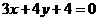 或
或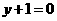 (D)
(D)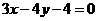 或
或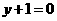
(6)如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论不成立的是
 (A)BC∥平面PDF (B)DF⊥平面PAE
(A)BC∥平面PDF (B)DF⊥平面PAE
(C)平面PDF⊥平面PAE (D)平面PDE⊥平面ABC
(7)已知函数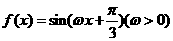 的最小正周期为
的最小正周期为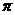 ,则该函数的图象
,则该函数的图象
(A)关于直线 对称 (B)关于点(
对称 (B)关于点( )对称
)对称
(C)关于直线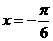 对称 (D)关于点(
对称 (D)关于点( )对称
)对称
(8)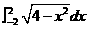 的值是
的值是
(A) (B)
(B)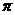
(C) (D)
(D)
 (9)如图,F为抛物线
(9)如图,F为抛物线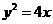 的焦点,A、B、C为该抛物线上三点,若
的焦点,A、B、C为该抛物线上三点,若 ,则
,则 等于
等于
(A)6 (B)4
(C)3 (D)2
(10)已知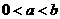 ,且
,且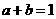 ,下列不等式成立的是
,下列不等式成立的是
(A)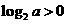 (B)
(B)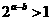
(C) (D)
(D)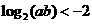
第Ⅱ卷
(17)(本小题满分12分)
在△ABC中, ,
,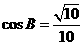 .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,求
,求 .
.
(18)(本小题满分12分)
下表为某班英语及数学成绩公布,全班共有学生50人,成绩分为1~5五个档次,设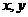 分别表示英语成绩和数学成绩,例如表中英语成绩为5分的共6人,数学成绩为3分的共15人.
分别表示英语成绩和数学成绩,例如表中英语成绩为5分的共6人,数学成绩为3分的共15人.
(Ⅰ) 的概率是多少?
的概率是多少? 且
且 的概率是多少?
的概率是多少? 的概率是多少?
的概率是多少?
在 的基础上,
的基础上, 同时成立的概率是多少?
同时成立的概率是多少?
(Ⅱ) 的概率是多少?
的概率是多少? 的值是多少?
的值是多少?
  |
5 |
4 |
3 |
2 |
1 |
|
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
3 |
2 |
1 |
0 |
9 |
3 |
|
2 |
1 |
 |
6 |
0 |
 |
|
1 |
0 |
0 |
1 |
1 |
3 |
 (19)(本小题满分12分)
(19)(本小题满分12分)
如图,在直三棱柱 中,
中,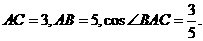
(Ⅰ)求证: ;
;
(Ⅱ)若D是AB的中点,求证: ∥平面
∥平面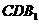 .
.
(20)(本小题满分12分)
已知等差数列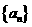 的前三项为
的前三项为 记前
记前 项和为
项和为
(Ⅰ)设 ,求
,求 和
和 的值;
的值;
(Ⅱ)设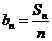 ,求
,求 的值.
的值.
(21)(本小题满分14分)
设A、B分别为椭圆 的左、右顶点,(
的左、右顶点,( )为椭圆上一点,椭圆的长半轴的长等于焦距.
)为椭圆上一点,椭圆的长半轴的长等于焦距.
(Ⅰ)求椭圆的方程;
(Ⅱ)设 ,若直线AP,BP分别与椭圆相交于异于A、B的点M、N,
,若直线AP,BP分别与椭圆相交于异于A、B的点M、N,
求证: 为钝角.
为钝角.
(22)(本小题满分14分)
已知函数
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设 ,函数
,函数 .若对任意
.若对任意 ,总存在
,总存在 ,使
,使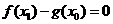 ,求实数
,求实数 的取值范围.
的取值范围.
(11)对总数为 的一批零件进行检验,现抽取一个容量为45的样本,若每个零件被抽取的可能性为25%,则零件的总数
的一批零件进行检验,现抽取一个容量为45的样本,若每个零件被抽取的可能性为25%,则零件的总数 等于
.
等于
.
 (12)在如右图所示的程序框图中,当程序被执行后,输出
(12)在如右图所示的程序框图中,当程序被执行后,输出 的结果是
.
的结果是
.
(13)化简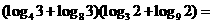 .
.
(14)已知向量 ,若向量
,若向量 平行,则实数
平行,则实数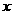 等于 .
等于 .
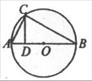 (15)如图,圆O上一点C在直径AB上的射影为D,若CD=4,BD=8,用圆O的半径等于 .
(15)如图,圆O上一点C在直径AB上的射影为D,若CD=4,BD=8,用圆O的半径等于 .
(16)设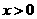 ,则
,则 的最大值等于 .
的最大值等于 .
(1)复数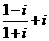 等于
等于
(A) (B)0
(C)
(B)0
(C) (D)1
(D)1
(2)设变量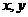 满足约束条件
满足约束条件 ,则目标函数
,则目标函数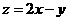 的最小值为
的最小值为
(A)7 (B)4
(C) (D)
(D)
(3)设集合 ,则
,则
(A) (B)
(B)
(C)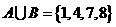 (D)
(D)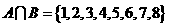
(4)在等比数列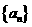 中,
中, ,则
,则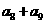 等于
等于
(A)90 (B)30
(C)70 (D)40
(5)若圆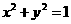 与直线
与直线 相切,则
相切,则 的值等于
的值等于
(A)5 (B)
(C)5或 (D)
(D)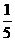 或
或
(6)已知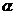 表示一个平面,
表示一个平面, 表示一条直线,则平面
表示一条直线,则平面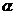 内至少有一条直线与
内至少有一条直线与
(A)平行 (B)相交
(C)异面 (D)垂直
(7)已知函数 的最小正周期为2
的最小正周期为2 ,则该函数的图象
,则该函数的图象
(A)关于直线 对称 (B)关于点(
对称 (B)关于点( )对称
)对称
(C)关于直线 对称 (D)关于点(
对称 (D)关于点(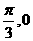 )对称
)对称
(8)在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于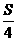 的概率是
的概率是
(A) (B)
(B)
(C) (D)
(D)
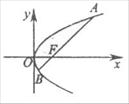 (9)如图,过抛物线
(9)如图,过抛物线 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于 、
、 ,若
,若 ,那么
,那么 等于
等于
(A)8 (B)7
(C)6 (D)4
(10)若 ,则
,则 的大小关系是
的大小关系是
(A) (B)
(B)
(C) (D)
(D)
第Ⅱ卷
22.(本小题满分12分)数列 中,
中, ,且前
,且前 项和
项和 满足
满足 ,
,
(1)求 ;
;
(2)令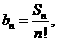 数列
数列 的前
的前 项和为
项和为 ,当
,当 时,求证:
时,求证: 。
。
2009届高中毕业班第三次模拟考试题
21.(本小题满分12分)
已知点 是平面上一动点,且满足
是平面上一动点,且满足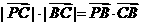
(1)求点 的轨迹C对应的方程;
的轨迹C对应的方程;
(2)已知点 在曲线C上,过点A作曲线C的两条弦
在曲线C上,过点A作曲线C的两条弦 ,且
,且 的斜率
的斜率 =2试推断:动直线
=2试推断:动直线 是否过定点?证明你的结论。
是否过定点?证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com