
题目列表(包括答案和解析)
4. 函数 的图像大致为
的图像大致为

A B C D
3. “ ”是“线
”是“线 与圆
与圆 相交”的
相交”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2. 设向量 ,
,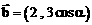 ,且
,且 ∥
∥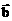 ,则锐角
,则锐角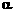 为
为
A. B.
B.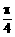 C.
C. D.
D.
一项是符合题目要求的。
1. 已知 ,i不虚数单位,若
,i不虚数单位,若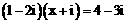 ,则x的值等于
,则x的值等于
A. B.
B. C.2 D.6
C.2 D.6
21.选做题:本题有(I)、(II)、(III)三个选答题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题记分。
(I)选修4-2:短阵与变换
求出曲线 作用下变换得到的曲线方程
作用下变换得到的曲线方程
(II)选修4-4:坐标系与参数方程
求经过极点且圆心的极坐标为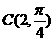 的圆C的极坐标方程。
的圆C的极坐标方程。
(III)选修4-5:不等式选讲
已知
20.(本小题满分14分)
已知 处的切线。
处的切线。
(I)求l的方程;
(II)若切线l与曲线 有且只有一个公共点,求a的值;
有且只有一个公共点,求a的值;
(III)证明:对于任意的 总有单调递减区间,并求出
总有单调递减区间,并求出 的单调递减区间的长度的取值范围。(区间
的单调递减区间的长度的取值范围。(区间 )
)
19.(本小题满分13分)
如图,在椭圆 中,F1,F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆在第一象限内的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD。
中,F1,F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆在第一象限内的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD。
(I)求a的值;
(II)若四边形EBCF2为平行四边形,求点C的坐标。
 (III)设
(III)设 的取值范围。
的取值范围。
18.(本小题满分13分)
甲、乙两人共同抛掷一枚硬币,规定硬币正面朝上甲得1分,否则乙得1分,先积得3分者获胜,并结束游戏。
(I)求在前3次抛掷中甲得2分,乙得1分的概率;
(II)若甲已经积得2分,乙已经积得1分,求甲最终获胜的概率;
(III)用ξ表示决出胜负抛硬币的次数,求ξ的分布列及数学期望。
17.(本小题满分13分)
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,
∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点。
(I)若点E是棱CC1的中点,求证:EF//平面A1BD;
 (II)试确定点E的位置,使得A1-BD-E为直二面角,并说明理由。
(II)试确定点E的位置,使得A1-BD-E为直二面角,并说明理由。
16.(本小题满分13分)
已知 的最小正周期为
的最小正周期为 。
。
(I)求 的单调递增区间;
的单调递增区间;
(II)求 的最大值和最小值。
的最大值和最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com