
题目列表(包括答案和解析)
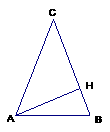
5. 如图,在 中,
中, ,
, ,则过点
,则过点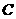 ,以
,以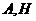 为
为
两焦点的双曲线的离心率为
A.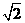 |
B.2 |
C.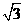 |
D.3 |
4.函数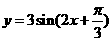 的图象按向量
的图象按向量 平移后所得的图像关于点
平移后所得的图像关于点 中心对称,则向量
中心对称,则向量 的坐标可能为
的坐标可能为
A. |
B.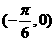 |
C. |
D.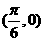 |
3. 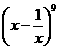 的展开式的第3项是
的展开式的第3项是
A.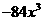 |
B. |
C. |
D.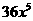 |
2. 已知{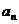 }是等差数列,
}是等差数列, ,
, ,
则过点
,
则过点 ,
, 的直线的斜率为
的直线的斜率为
|
A.4 |
B.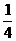 |
C. |
D. |
1.若复数 (其中
(其中 为虚数单位),则
为虚数单位),则 等于
等于
A. |
B.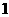 |
C. 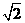 |
D.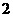 |
22. (14分)已知三点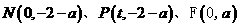 ,(其中
,(其中 为大于零的常数,为参数),平面捏动点M满足
为大于零的常数,为参数),平面捏动点M满足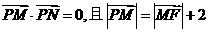
(1)求动点M的轨迹方程;
(2)若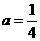 时,过点M的轨迹上任意一点A,作圆
时,过点M的轨迹上任意一点A,作圆 的两条切线,分别交点M的轨迹于B、C两点,连结BC,试证明BC是圆
的两条切线,分别交点M的轨迹于B、C两点,连结BC,试证明BC是圆 的切线。
的切线。
本资料由《七彩教育网》 提供!
21. (12分)已知数列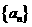 的前
的前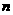 项和为
项和为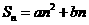 ,其中
,其中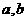 是常数,且
是常数,且
(1)求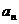 ,并证明
,并证明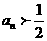
(2)当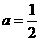 时,设数列
时,设数列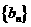 满足
满足
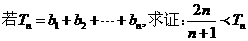
20.(12分)将6个相同的球通过抛2枚均匀硬币的方式全部放入编号1、2、3的三个盒子里,若抛2枚硬币的结果均是正面向上,则1号盒内放入1个球;若2枚硬币均是反面向上,则2号盒内放入1个球;若2枚硬币一枚正面向上,另一枚反面向上,则3号盒内放入1个球,如此将6个小球全部放入盒中,最终1、2、3号盒的球数分别是
(1)求每个盒内的球数不小于该盒子的编号的概率;
(2)求 且
且 成等差数列的概率;
成等差数列的概率;
(3)求的期望值。
19. (12分)已知 为函数
为函数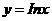 图像上的有点,O为坐标原点,记直线OP的斜率
图像上的有点,O为坐标原点,记直线OP的斜率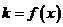 ,
,
(1)求证:当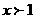 时,
时,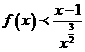
(2)某同学发现:总存在正实数 ,使
,使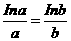 试问:他的判断是否正确?若不正确,请说明理由;若正确,请求出
试问:他的判断是否正确?若不正确,请说明理由;若正确,请求出 的取值范围。
的取值范围。
18.(12分)在三棱柱 中,侧面
中,侧面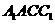 是矩形,
是矩形,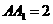 ,
,
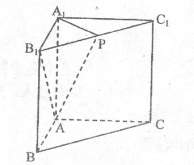 平面
平面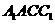
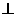 平面
平面 ,
, ,P是
,P是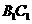 的中点,
的中点,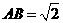
(1)求证: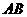
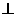
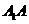
(2)求二面角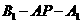 的正切值。
的正切值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com