18．(本小题满分12分)

　　　　 某校有一贫困学生因病需手术治疗，但现在还差手术费1.1万元。团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动。凡捐款10元便可享受一次摇奖机会，如图是摇奖机的示意图，摇奖机的旋转盘是均匀的，扇形区域A，B，C，D，E所对应的圆心角的比值分别为1：2：3：4：5。相应区域分别设立一、二、三、四、五等奖，奖品分别为价值5元、4元、3元、2元、1元的学习用品。摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域(边线忽略不计)即可获得相应价值的学习用品(如图指针指向区域，可获得价值3元的学习用品)。

　 (1)预计全校捐款10元者将会达到1500人次，那么除去购买学习用品的款项后，剩余款项是否能帮助该生完成手术治疗？

　 (2)如果学生甲捐款20元，获得了两次摇奖机会，求他获得价值6元时的学习用品的概率。

17．(本小题满分12分)

设函数。

　 (1)写出函数的最小正周期及单调递减区间；

　 (2)当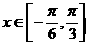时，函数的最大值与最小值的和为，求的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积。

16．电视机的使用寿命与显像管开关的次数有关。某品牌的电视机的显像管开关了10000次还能继续使用的概率是0.96，开关了15000次后还能继续使用的概率是0.80，则已经开关了10000次的电视机显像管还能继续使用到15000次的概率是　　　　　　　 。

15．已知抛物线

　　　　　　　　　 。

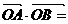14．在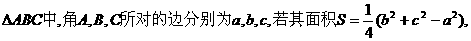

=　　　　　　　　　 。

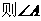13．由代数式的乘法法则类比推导向量的数量积的运算法则：

①“mn=nm”类比得到“a·b=b·a”；

②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”；

③“t≠0，mt=nt”类比得到“”；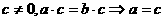

④“”类比得到“”。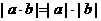

以上类比得到的正确结论的序号是　　　　　　　 (写出所有正确结论的序号)。

12．一支足球队每场比赛获胜(得3分)的概率为a，与对手踢平(得1分)的概率为b，负于对手(得0分)的概率为c(a，b，c∈(0，1))，已知该足球队进行一场比赛得分的期望是1，则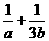的最小值为　　　　　　　　 (　　 )

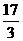　　　 A．　　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　 D．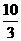

第Ⅱ卷(非选择题　 共90分)

11．已知在平面直角坐标系满足条件

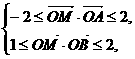　　 　则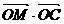的最大值为　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．－1　　　　　　　　　　 B．0　　　　　　　　　　　　 C．3　　　　　　　　　　　　 D．4

10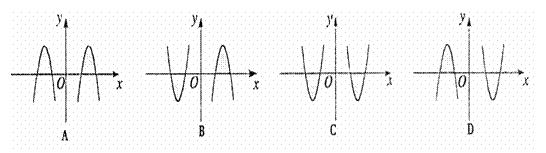．已知函数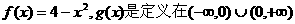上的奇函数，当x>0时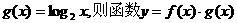，的大致图象为　　　　　　　　　　　　　　　　　　　　　 (　　 )

9．给出下列四个命题，其中正确的一个是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．在线性回归模型中，相关指数R²=0.80，说明预报变量对解释变量的贡献率是80%

　　　 B．在独立性检验时，两个变量的2×2列表中对角线上数据的乘积相差越大，说明这两个变量没有关系成立的可能性就越大

　　　 C．相关指数R²用来刻画回归效果，R²越小，则残差平方和越大，模型的拟合效果越好

　　　 D．随机误差e是衡量预报精确度的一个量，它满足E(e)=0