
题目列表(包括答案和解析)
2.设数列 满足
满足 ,若
,若 是等差数列,
是等差数列, 是等比数列.
是等比数列.
(1)分别求出数列 的通项公式;(2)求数列
的通项公式;(2)求数列 中最小项及最小项的值;
中最小项及最小项的值;
(3)是否存在 ,使
,使 ,若存在,求满足条件的所有
,若存在,求满足条件的所有 值;若不存在,请说明理由.
值;若不存在,请说明理由.
解:(1) 由
由 成等差数列知其公差为1,
成等差数列知其公差为1,
故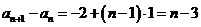
 由
由 等比数列知,其公比为
等比数列知,其公比为 ,故
,故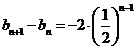
 =
=
 +6=
+6=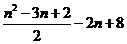 =
=
 =
=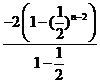 +6=2+
+6=2+
(2)由(1)题知,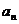 =
= ,所以当
,所以当 或
或 时,
时,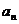 取最小项,其值为3
取最小项,其值为3
(3)假设 存在,使
存在,使
 -2-
-2- =
= -
-

则
 -
-
 即
即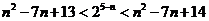
∵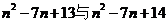 是相邻整数
是相邻整数
∴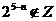 ,这与
,这与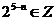 矛盾,所以满足条件的
矛盾,所以满足条件的 不存在
不存在
1.解:(Ⅰ)依题意,得 .于是,当
.于是,当 时,有
时,有 .
.
两式相减,得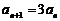 (
( ). 又因为
). 又因为 ,
,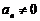 ,所以数列
,所以数列 是首项为
是首项为 、公比为3的等比数列. 因此,
、公比为3的等比数列. 因此, (
(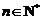 );
);
(Ⅱ)因为 ,所以
,所以 .
.
要使 为等比数列,当且仅当
为等比数列,当且仅当 ,即
,即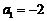 .
.
5.解:(1)∵ ,∴
,∴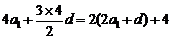 ,解得
,解得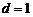 ;
;
(2)∵ ,∴数列
,∴数列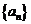 的通项公式为
的通项公式为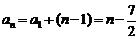 ,∴
,∴
∵函数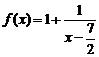 在
在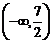 和
和 上分别是单调减函数,∴
上分别是单调减函数,∴ 当
当 时,
时,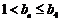
∴数列 中的最大项是
中的最大项是 ,最小项是
,最小项是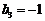
(2)由 得
得 又函数
又函数 在
在 和
和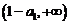 上分别是单调减函数,且
上分别是单调减函数,且 时
时 ;
; 时
时 .∵对任意的
.∵对任意的 ,都有
,都有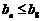 ,∴
,∴ ∴
∴ ∴
∴ 的取值范围是
的取值范围是
赣马高级中学解答题专题训练9答案
4.解:(Ⅰ)证明:由题设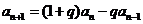 (
(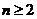 ),得
),得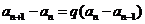 ,即
,即 ,
,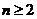 .又
.又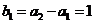 ,
, ,所以
,所以 是首项为1,公比为
是首项为1,公比为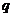 的等比数列.
的等比数列.
(Ⅱ)解法:由(Ⅰ)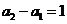 ,
, ,……,
,……,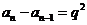 ,(
,(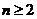 ).
).
将以上各式相加,得 (
(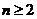 ).
).
所以当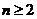 时,
时,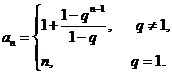 上式对
上式对 显然成立.
显然成立.
(Ⅲ)解:由(Ⅱ),当 时,显然
时,显然 不是
不是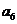 与
与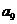 的等差中项,故
的等差中项,故 .
.
由 可得
可得 ,由
,由 得
得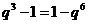 , ①
, ①
整理得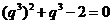 ,解得
,解得 或
或 (舍去).于是
(舍去).于是 .
.
另一方面,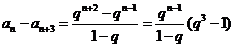 ,
, .
.
由①可得 ,
,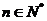 .所以对任意的
.所以对任意的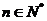 ,
,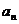 是
是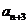 与
与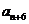 的等差中项.
的等差中项.
3.数列 的前
的前 项和为
项和为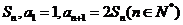 。(1)求数列
。(1)求数列 的通项
的通项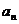 ;(2)求数列
;(2)求数列 的前
的前 项和
项和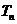 。
。
解:(1)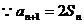 ,
, 
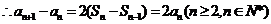 ,即
,即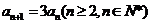
 数列
数列 从第2项起构成以3为公比的等比数列,
又
从第2项起构成以3为公比的等比数列,
又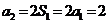

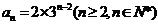 又
又 不符合上式,所以,数列
不符合上式,所以,数列 的通项
的通项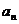
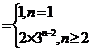 (
( (2)
(2)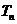 =
=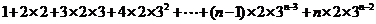
又3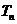 =
=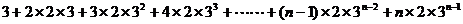
两式相减得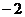
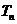 =
=
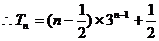
2.
数列{an}的前n项和记为Sn,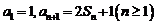 (I)求{an}的通项公式;
(I)求{an}的通项公式;
(II)等差数列{bn}的各项为正,其前n项和为Tn,且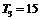 ,又
,又 成等比数列,求Tn
成等比数列,求Tn
(I)由 可得
可得 , 两式相减得
, 两式相减得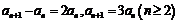 又
又 ∴
∴ ,故{an}是首项为1,公比为3得等比数列 ∴
,故{an}是首项为1,公比为3得等比数列 ∴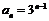 .
.
(II)设{bn}的公差为d,由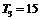 得,可得
得,可得 ,可得
,可得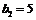 ,故可设
,故可设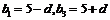
又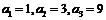 由题意可得
由题意可得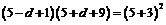 解得
解得
∵等差数列{bn}的各项为正,∴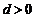 ,∴
,∴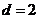 …∴
…∴
1.解: 若 , 则
, 则 ,
, 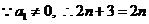 , 不合要求;
, 不合要求;
若 , 则
, 则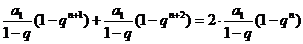 ,
, 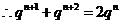 ,
,
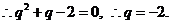 综上,
综上,  .
.
4.已知数列 的前n项和为
的前n项和为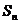 ,当
,当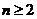 时,点
时,点 在
在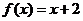 的图像上, 且
的图像上, 且 .
.
(Ⅰ)求数列 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 的最大值及相应的n值.
的最大值及相应的n值.
解: (Ⅰ)∵点 在
在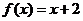 的图像上,
的图像上, 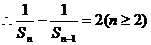
 公差为2的等差数列
公差为2的等差数列
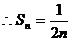
当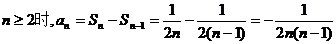
当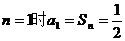

(Ⅱ)由已知得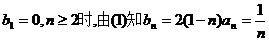
 。当且仅当n=1时,
。当且仅当n=1时, 。
。
练习1:已知 是一个等差数列,且
是一个等差数列,且 ,
,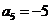 .(Ⅰ)求
.(Ⅰ)求 的通项
的通项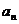 ; (Ⅱ)求
; (Ⅱ)求 前n项和Sn的最大值.解:(Ⅰ)设
前n项和Sn的最大值.解:(Ⅰ)设 的公差为
的公差为 ,由已知条件,
,由已知条件, ,解出
,解出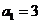 ,
, .
.
所以 .(Ⅱ)
.(Ⅱ)
 .所以
.所以 时,
时,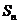 取到最大值
取到最大值 .练习2:设
.练习2:设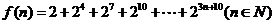 ,则
,则 =
=
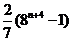 ;
;
赣马高级中学解答题专题训练8答案
3.已知数列 的前
的前 项和
项和 .求数列{
.求数列{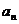 }的通项公式;
}的通项公式;
解:  时,
时, ; 当
; 当 .
.
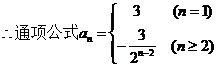
2.已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项。
解析:
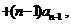 (n≥2),
(n≥2), (n≥3)两式相减,得
(n≥3)两式相减,得 推广
推广
 当n=2时, a2=a1
当n=2时, a2=a1
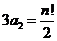 。练习:在数列{an}中,若a1+a2+…+an=2n,求
。练习:在数列{an}中,若a1+a2+…+an=2n,求 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com