
题目列表(包括答案和解析)
4.已知函数
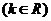 是偶函数.
是偶函数.
(1) 求 的值;
的值;
(2) 设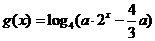 ,若函数
,若函数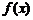 与
与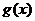 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数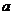 的取值范围.
的取值范围.
3.已知函数 ,
,
(1)讨论函数 的奇偶性,并说明理由。
的奇偶性,并说明理由。
(2)若函数 在
在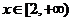 上是增函数,求
上是增函数,求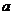 的取值范围。
的取值范围。
2.已知关于 的不等式
的不等式 >2的解集为A,且5
>2的解集为A,且5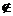 A.
A.
(1)求实数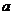 的取值范围
的取值范围
(2)求集合A
1。已知函数 的定义域为
的定义域为 ,
(1)求M(2)当
,
(1)求M(2)当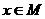 时,求
时,求
 的最小值.
的最小值.
6.如图,设动点P在棱长为1的正方体 的对角线
的对角线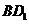 上,记
上,记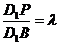 .
.
 当
当 为钝角时,求
为钝角时,求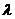 的取值范围.
的取值范围.
解:由题设可知,以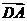 、
、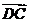 、
、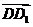 为单位正交基底,
为单位正交基底,
建立如图所示的空间直角坐标系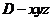 ,
,
则有 ,
,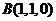 ,
, ,
,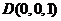
由 ,得
,得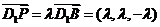 ,所以
,所以
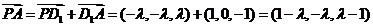
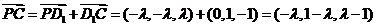
显然 不是平角,所以
不是平角,所以 为钝角等价于
为钝角等价于
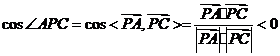 ,则等价于
,则等价于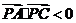
即 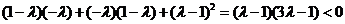 ,得
,得
因此,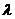 的取值范围是
的取值范围是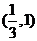
5.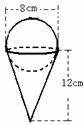 一个圆锥形的空纸杯上面抹着一个球形的冰淇淋,尺寸如图,如果冰淇淋融化了,会溢出杯子吗?说明理由
一个圆锥形的空纸杯上面抹着一个球形的冰淇淋,尺寸如图,如果冰淇淋融化了,会溢出杯子吗?说明理由
解:会溢出。冰淇淋的体积是 ,空纸杯的容积
,空纸杯的容积 ,
,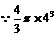
 ,所以,冰淇淋融化了,会溢出杯子。
,所以,冰淇淋融化了,会溢出杯子。
4. 如图所示,有一圆锥形酒杯,其底面半径等于酒杯圆锥体的高,若以9
如图所示,有一圆锥形酒杯,其底面半径等于酒杯圆锥体的高,若以9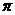 cm3/s的速度向该酒杯倒酒,则酒深10cm时酒面上升的速度为 cm/s.
cm3/s的速度向该酒杯倒酒,则酒深10cm时酒面上升的速度为 cm/s.
解:设酒面高度为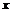 ,则酒酒面圆的半径为
,则酒酒面圆的半径为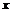 ,酒的即时体积
,酒的即时体积 ,
, .
. ,
, 。当
。当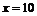 ,
, ,解得,
,解得, 。酒深10cm时酒面上升的速度即酒深
。酒深10cm时酒面上升的速度即酒深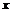 在
在 时刻的导数是
时刻的导数是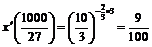 。
。
3.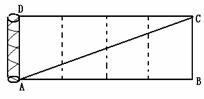 有一根长为
有一根长为 ,底面半径为1的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,使铁丝两端落在同一条母线的两端,则铁丝的长度最少为
,底面半径为1的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,使铁丝两端落在同一条母线的两端,则铁丝的长度最少为
解:把圆柱体侧面展开4次,如图。AB=8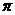 ,BC=
,BC= ,点A和C是铁丝的起止位置,AC的长度就是铁丝的最短长度。
,点A和C是铁丝的起止位置,AC的长度就是铁丝的最短长度。 。铁丝的最短长度为10
。铁丝的最短长度为10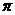 .
.
2.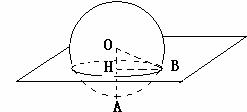 湖面上漂浮着一个丢弃的蓝球,当湖面结冰后将球取出,冰面上留下一个直径为24,深为8的球坑,则该蓝球的体积是
湖面上漂浮着一个丢弃的蓝球,当湖面结冰后将球取出,冰面上留下一个直径为24,深为8的球坑,则该蓝球的体积是
解:如图,球坑的半径为12,相当于冰面与球体形成的截面圆的半径12,球心O到截面圆的距离为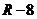 ,
,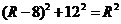 ,解得
,解得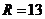 。该球的体积是
。该球的体积是
1.某球的外切圆台上下底面半径分别为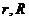 ,求该球的体积
,求该球的体积
 解:研究轴截面如图,得到等腰梯形和内切圆,根据切线长定理,腰长为
解:研究轴截面如图,得到等腰梯形和内切圆,根据切线长定理,腰长为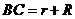 ;根据勾股定理,
;根据勾股定理,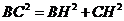 ,
, ,其中球的半径为
,其中球的半径为 ,解得
,解得 ,该球的体积
,该球的体积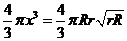 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com