
题目列表(包括答案和解析)
3. 某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备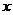 年的年平均污水处理费用
年的年平均污水处理费用 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
2.已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若AÌ∁RB,求实数m的取值范围.
1.已知集合 ,
, .
.
(Ⅰ)若 ,求实数
,求实数 的值;(Ⅱ)若
的值;(Ⅱ)若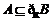 ,求实数
,求实数 的取值范围.
的取值范围.
5.经市场调查,某种商品在过去50天的销售和价格均为销售时间 (天)的函数,且销售量近似地满足
(天)的函数,且销售量近似地满足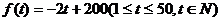 ,前30天价格为
,前30天价格为 ,后20天价格为
,后20天价格为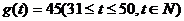 。
。
(1) 写出该种商品的日销售 与时间
与时间 的函数关系;
的函数关系;
(2) 求日销售S的最大值。
赣马高级中学解答题专题训练11
不等式(一) 编写:朱孟习 审核:王怀学
4. 已知二次函数f(x)的二次项系数为a(a<0),且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
3.已知动点 与定点
与定点 在直线
在直线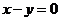 的同侧。
的同侧。
(1)写出关于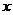 的不等式;
的不等式;
(2) 是这个不等式的解,求
是这个不等式的解,求 的取值范围。(3)已知
的取值范围。(3)已知 ,求这个关于
,求这个关于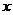 的不等式的解集。
的不等式的解集。
2.已知函数
(1)求证:函数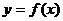 在(0,
在(0, )上是增函数;
)上是增函数;
(2)若 在[1,
在[1, ]上恒成立,求实数a的取值范围
]上恒成立,求实数a的取值范围
1. 设不等式组表示的区域为A,不等式组表示的区域为B.
(1)在区域A中任取一点(x,y),求点(x,y)∈B的概率;
(2)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)在区域B中的概率
4.
1.解:(Ⅰ)∵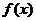 定义域为
定义域为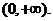
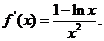 ∵
∵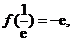 又∵
又∵
∴函数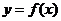 在
在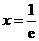 处的切线方程为:
处的切线方程为: 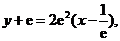 即:
即:
(Ⅱ)令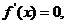 得
得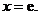 ∵当
∵当 时,
时,
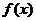 在
在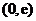 上为增函数;
上为增函数;
当 时,
时,
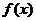 在
在 上为减函数; ∴
上为减函数; ∴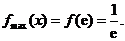
2解:(Ⅰ) ,则
,则 或
或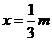 ,
,
当x变化时, 与
与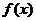 的变化情况如下表:
的变化情况如下表:
 |
(-∞,-m) |
-m |
(-m,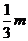 ) ) |
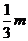 |
(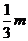 ,+∞) ,+∞) |
 ) ) |
+ |
0 |
- |
0 |
+ |
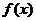 |
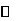 |
极大值 |
 |
极小值 |
 |
从而可知,当 时,函数
时,函数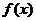 取得极大值9,即
取得极大值9,即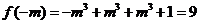
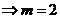 .
.
(Ⅱ)由(Ⅰ)知,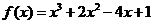 ,依题意知
,依题意知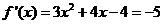 ,∴
,∴ 或
或
又 ,
, ,所以切线方程为
,所以切线方程为 ),或
),或 ,
,
即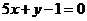 ,或
,或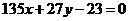 .
.
3解.(Ⅰ) 
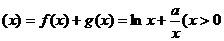


由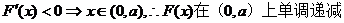 。
。
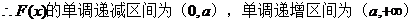
(Ⅱ)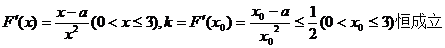
 当
当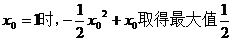
 ………………………………………
………………………………………
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com