
题目列表(包括答案和解析)
4.某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设 表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额). (1)该厂从第几年开始盈利?
表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额). (1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
解:由题意知
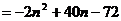 ………………2分
………………2分
(1)由 …………5分
…………5分
由 知,从经三年开始盈利.…………………………6分
知,从经三年开始盈利.…………………………6分
(2)方案①:年平均纯利润 当且仅当n=6时等号成立.
当且仅当n=6时等号成立.
故方案①共获利6×16+48=144(万元),此时n=6.………………8分
方案②: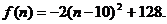 当n=10,
当n=10,
故方案②共获利128+16、144(万元)……………………10分
比较两种方案,获利都是144万元,但由于第①种方案只需6年,而第②种方案需10年,故选择第①种方案更合算.…………………………12分
3. 某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.(1)求该企业使用该设备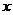 年的年平均污水处理费用
年的年平均污水处理费用 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
解:(1)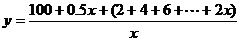 即
即 (
( );----7分
);----7分
(不注明定义域不扣分,或将定义域写成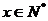 也行)
也行)
(2)由均值不等式得: (万元)--------11分
(万元)--------11分
当且仅当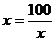 ,即
,即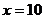 时取到等号. -------------------13分
时取到等号. -------------------13分
答:该企业10年后需要重新更换新设备.------------------------------------------14分
2.已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若AÌ∁RB,求实数m的取值范围.
由已知得A=[-2,4],B=[m-3,m].
(1)∵A∩B=[2,4],∴∴m=5.
(2)∵B=[m-3,m],∴∁RB=(-∞,m-3)∪(m,+∞).
∵AÌ∁RB,∴m-3>4或m<-2.∴m>7或m<-2.∴m∈(-∞,-2)∪(7,+∞).
1.已知集合 ,
, .
.
(Ⅰ)若 ,求实数
,求实数 的值;(Ⅱ)若
的值;(Ⅱ)若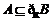 ,求实数
,求实数 的取值范围.
的取值范围.
解:由已知得: ,
,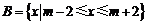 . ………………4分
. ………………4分
(Ⅰ)∵ , ∴
, ∴ ∴
∴ ∴
∴ .
.
(Ⅱ) 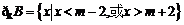 . ∵
. ∵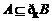 ,
,
∴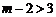 ,或
,或 , ∴
, ∴ 或
或 .
.
5.解:(1)根据题意得:
 ………………7分
………………7分
(2)①当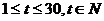 时,
时,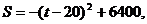
当 时,
时, 的最大值为
的最大值为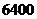 ………………………………10分
………………………………10分
②当 ,
, 时,
时,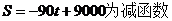 ,
,
 的最大值是
的最大值是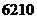 ……………………12分。
……………………12分。
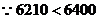 ,
,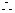 当
当 时,日销量额
时,日销量额 有最大值
有最大值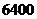 。
。
赣马高级中学解答题专题训练10
不等式(一) 编写:朱孟习 审核:王怀学
4. (1)因为f(x)+2x>0的解集为(1,3),所以f(x)+2x=a(x-1)(x-3),且a<0,因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a.①
由方程f(x)+6a=0得ax2-(2+4a)x+9a=0. ②
因为方程②有两个相等的根,所以△=2+4a)2-4a·9a=0,
即 5a2-4a-1=0,解得a=1或-.
由于a<0,所以舍去a=1.将a=-代入①得f(x)的解析式f(x)=-x2-x-.
(2)由f(x)=ax2-2(1+2a)x+3a=a(x-)2-.
及a<0,可得f(x)的最大值为-.
由解得 a<-2-或-2+<a<0.
故当f(x)的最大值为正数时,实数a的取值范围是(-∞,-2-) (-2+,0).
(-2+,0).
1. (1)设集合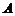 中的点
中的点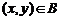 为事件
为事件 , 区域
, 区域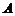 的面积为
的面积为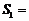 36, 区域
36, 区域 的面积为
的面积为 18
18
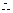
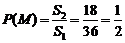 .
.
(2)设点 在集合
在集合 为事件
为事件 , 甲、乙两人各掷一次骰子所得的点数为36个,其中在集合
, 甲、乙两人各掷一次骰子所得的点数为36个,其中在集合 中的点有21个,故
中的点有21个,故 .
.
2解:(1)
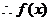 在(0,
在(0, )上为增函数
)上为增函数
(注:定义法相应给分)
(2)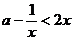 在[1,
在[1, )上恒成立 设
)上恒成立 设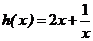
则 在[1,
在[1, )上恒成立
)上恒成立 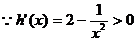
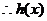 在[1,
在[1, ]上单调递增
]上单调递增  故
故 即
即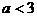
 的取值范围为(
的取值范围为( ,3)
,3)
3解:(1)∵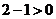 ∴
∴ 可化为
可化为 ,
,
即 ………………………………………………………………2分
………………………………………………………………2分
(2)∵-1是不等式的解 ∴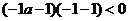 ∴
∴ ……………………4分
……………………4分
(3)当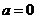 时,不等式的解集为
时,不等式的解集为 ………………………………………………6分
………………………………………………6分
当 时,方程
时,方程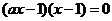 有两个根
有两个根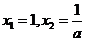 ……………………………………8分
……………………………………8分
若 时,即
时,即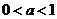 ,不等式的解集为
,不等式的解集为 …………………………10分
…………………………10分
若 时,即
时,即 ,不等式的解集为
,不等式的解集为 …………………………………………12分
…………………………………………12分
若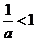 时,即
时,即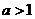 ,不等式的解集为
,不等式的解集为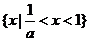 ………………………………14分
………………………………14分
所以,当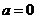 时,不等式的解集为
时,不等式的解集为
当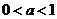 时,不等式的解集为
时,不等式的解集为
当 时,不等式的解集为
时,不等式的解集为
当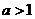 时,不等式的解集为
时,不等式的解集为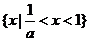 ………………………………………16分
………………………………………16分
6.数列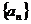 的前n项和记为
的前n项和记为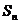 ,已知
,已知 ,
,
(1)证明数列 是公比为2的等比数列。
是公比为2的等比数列。
(2)求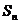 关于n的表达式。(3)请猜测是否存在自然数
关于n的表达式。(3)请猜测是否存在自然数 ,对于所有的
,对于所有的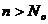 有
有 恒成立,并证明。
恒成立,并证明。
赣马高级中学解答题专题训练9答案
不等式1 编写:朱孟习 审核:王怀学
5. 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,
DE的位置应在哪里?如果DE是参观线路,则希望它最长,
DE的位置又应在哪里?请予证明.
4.某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设 表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com