
题目列表(包括答案和解析)
18. (命题人:启东中学李俊,审题人:启东中学曹瑞彬,原创)
设顶点为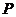 的抛物线
的抛物线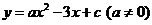 交
交 轴正半轴于
轴正半轴于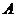 、
、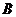 两点,交
两点,交 轴正半轴于
轴正半轴于 点,圆
点,圆 (圆心为
(圆心为 )过
)过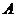 、
、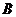 、
、 三点,恰好与
三点,恰好与 轴相切. 求证:
轴相切. 求证: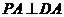 .
.
解:设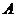 、
、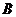 、
、 三点的坐标为
三点的坐标为 ,
, ,
, ,圆
,圆 的圆心坐标为
的圆心坐标为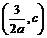 ,
,
由韦达定理,知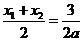 . 原点
. 原点 到圆D的切线为
到圆D的切线为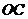 ,所以
,所以
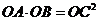 ,即
,即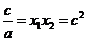 . 故
. 故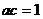 .
.
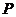 点坐标为
点坐标为  . 由(1),
. 由(1),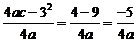 .
.
设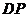 交
交 轴于
轴于 ,要证
,要证 与圆
与圆 相切,即证
相切,即证  .
.
如果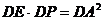 ,那么
,那么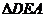 与
与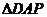 相似,
相似, .
.
所以只需证 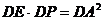 .而
.而  ,
,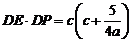 ,
,
所以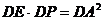 等价于
等价于 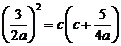 ,即只需要证
,即只需要证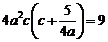 .
.
由 ,
,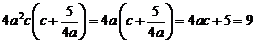 ,所以
,所以 与圆
与圆 相切.
相切.
17. (命题人:启东中学曹瑞彬,审题人:启东中学李俊,原创)
在数列{an}中,已知,a1=2,an+1+ an+1 an-2 an.对于任意正整数 ,
,
(Ⅰ)求数列{an}的通项an的表达式;
(Ⅱ)若 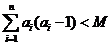 (
(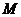 为常数,且为整数),求
为常数,且为整数),求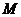 的最小值.
的最小值.
解:(Ⅰ)由题意,对于n∈N*, ,且
,且 ,即
,即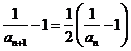 .
.
由  ,得
,得  .则数列
.则数列 是首项为
是首项为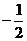 ,公比为
,公比为 的等比数列.于是
的等比数列.于是 , 即
, 即 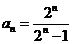 .
.
(Ⅱ)由(Ⅰ),得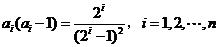 . 当
. 当 时,因为
时,因为
 ,
,
所以
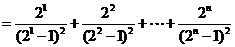

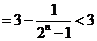 .
.
又
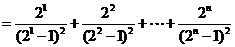
 ,故M的最小值为3.
,故M的最小值为3.
16.(命题人:南通中学赵栋,审题人:南通中学杨建楠,原创)
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf‘(x)-f(x)>0,对任意正数a、b,若a<b,则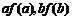 的大小关系为
.
的大小关系为
.
[解析]设 ,则
,则 ,故
,故 为增函数,由a<b,
为增函数,由a<b,
有 .
.
15. (命题人:南通中学田宇龙,审题人:南通中学杨建楠,原创)
已知实数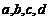 满足
满足 ,
, ,则
,则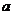 的取值范围是 .
的取值范围是 .
[解析]由柯西不等式,得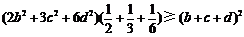 ,
,
即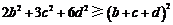 .由条件,得
.由条件,得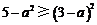 .
.
解得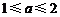 ,当且仅当
,当且仅当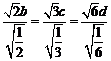 时等号成立.
时等号成立.
代入 时,
时,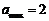 ;
;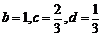 时,
时, .
.
所以,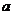 的取值范围是
的取值范围是 .
.
14. (命题人:南通中学田宇龙,审题人:南通中学杨建楠,原创)
极坐标系中,直线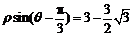 与曲线
与曲线 相交所得弦长为
.
相交所得弦长为
.
[解析]直线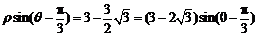 ,为过点
,为过点 且倾斜角为
且倾斜角为 的直线,而曲线
的直线,而曲线 表示的是一个椭圆;建立一个以椭圆的中心为原点的直角坐标系,则椭圆的标准方程为
表示的是一个椭圆;建立一个以椭圆的中心为原点的直角坐标系,则椭圆的标准方程为 ,直线的参数方程为
,直线的参数方程为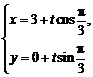 ,代入标准方程,得
,代入标准方程,得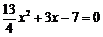 ,弦长为
,弦长为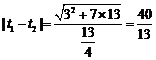 .
.
13.(命题人:海门中学黄卫平,审题人海门中学方伟)
当x=2时,下面这段程序输出的结果是___________.

End Whlie

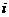
答案:13.
12. (命题人:通州中学薛国均,审题人:通州中学宋茂华,改编)
已知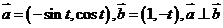 ,则
,则 的值______
的值______
[解析] ∵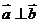 ,∴
,∴ ,∴
,∴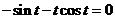 ,
,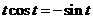 .
.
∴ =
=
=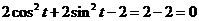 .
.
11. (命题人:通州中学薛国均,审题人:通州中学宋茂华,改编)
已知 的外接圆的圆心
的外接圆的圆心 ,
,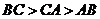 ,则
,则 的大小关系
的大小关系
为______.
[解析]设 的外接圆的半径为
的外接圆的半径为 ,
,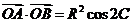 ,
,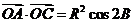 ,
,
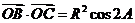 .
.
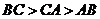 ,
, .
.
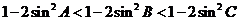 ,
,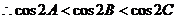 .
.

10. (命题人:通州中学薛国均,审题人:通州中学宋茂华,改编)
复数 ,满足
,满足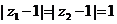 ,则
,则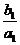 与
与 的大小关系是_________.
的大小关系是_________.
[解析]因为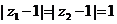 ,所以
,所以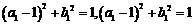 ,
, .
.
因为 ,所以
,所以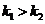 ,所以
,所以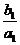

 .
.
9. (命题人:如东中学唐勇,审题人:如东中学何鹏,由《中学数学教学参考》2008年第2期题
目改编 )
打开“几何画板”软件进行如下操作:
①用画图工具在工作区画一个大小适中的圆C;
②用取点工具分别在圆C上和圆C外各取一个点A、B;
③用构造菜单下对应命令作出线段AB的垂直平分线l;
④作出直线AC.
设直线AC与直线l相交于点P,当点A在圆C上运动时,点P的轨迹是____________.
[解析]双曲线.由图可得,PC-PB=PC-PA=AC,或PB-PC=PA-PC=AC,
从而点P到定点B、C的距离之差的绝对值是定长AC,由双曲线定义即可得.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com