
题目列表(包括答案和解析)
5.已知=(sinθ,),=(1,),其中θ∈(π,),则一定有 ( )
A.∥ B.⊥ C.与夹角为45°D.||=||
4.设=(,sina),=(cosa,),且∥,则锐角a为 ( )
A.30° B.45° C.60° D.75°
3.已知△ABC中,=,=,若·<0,则△ABC是 ( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.任意三角形
2.将函数y=2sin2x-的图象按向量(,)平移后得到图象对应的解析式是 ( )
A.2cos2x B.-2cos2x C.2sin2x D.-2sin2x
1.已知=(cos40°,sin40°),=(cos20°,sin20°),则·= ( )
A.1 B. C. D.
在三角形的正弦定理与余弦定理在教材中是利用向量知识来推导的,说明正弦定理、余弦定理与向量有着密切的联系.解斜三角形与向量的综合主要体现为以三角形的角对应的三角函数值为向量的坐标,要求根据向量的关系解答相关的问题.
[例6] 已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若=(-cos,sin),=(cos,sin),a=2,且·=.
(Ⅰ)若△ABC的面积S=,求b+c的值.
(Ⅱ)求b+c的取值范围.
[分析] 第(Ⅰ)小题利用数量积公式建立关于角A的三角函数方程,再利用二倍角公式求得A角,然后通过三角形的面积公式及余弦定理建立关于b、c的方程组求取b+c的值;第(Ⅱ)小题正弦定理及三角形内角和定理建立关于B的三角函数式,进而求得b+c的范围.
[解] (Ⅰ)∵=(-cos,sin),=(cos,sin),且·=,
∴-cos2+sin2=,即-cosA=,
又A∈(0,π),∴A=.
又由S△ABC=bcsinA=,所以bc=4,
由余弦定理得:a2=b2+c2-2bc·cos=b2+c2+bc,∴16=(b+c)2,故b+c=4.
(Ⅱ)由正弦定理得:====4,又B+C=p-A=,
∴b+c=4sinB+4sinC=4sinB+4sin(-B)=4sin(B+),
∵0<B<,则<B+<,则<sin(B+)≤1,即b+c的取值范围是(2,4].
[点评] 本题解答主要考查平面向量的数量积、三角恒等变换及三角形中的正弦定理、余弦定理、面积公式、三角形内角和定理等.解答本题主要有两处要注意:第(Ⅰ)小题中求b+c没有利用分别求出b、c的值为解,而是利用整体的思想,使问题得到简捷的解答;(2)第(Ⅱ)小题的求解中特别要注意确定角B的范围.
[专题训练]
42.(命题人:如东丰利中学王琴, 审题人:如东丰利中学朱兵)
某校通过几次模拟测试发现高三年级物化班的三门总分与选修物化的匹配不理想,学校决定进行物理、化学两门功课的培训,每位同学可以选择参加一门、两门或不参加。已知选物理的有40%,选化学的有35%。假设每个人对功课的选择是相互独立的,且各人的选择相互没有影响。
(1)任选一位物化班学生,求该同学参加培训的概率。
(2)任选3名同学,记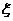 为3人中参加培训的人数,求
为3人中参加培训的人数,求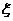 的分布列和期望。
的分布列和期望。
[解析]:任选一位物化班学生,记“该人参加物理培训”为事件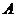 ,“该人参加化学培训”为事件
,“该人参加化学培训”为事件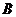 ,由题设知,事件
,由题设知,事件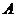 与
与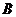 相互独立,且P(A)=0.4,P(B)=0.35.
相互独立,且P(A)=0.4,P(B)=0.35.
(1)任选一位物化班学生,该人没有参加过培训的概率是
P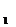 =(1- P(A))(1- P(B))=0.39
=(1- P(A))(1- P(B))=0.39
所以该人参加过培训的概率是P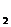 =1- P
=1- P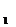 =0.61
=0.61
(2)因为每个人的选择是相互独立的,所以3人中参加过培训的人数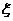 服从二项分布B(3,0.61),P(
服从二项分布B(3,0.61),P(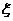 =k)=C
=k)=C 0.61
0.61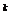 0.39
0.39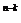 ,
,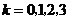 ,即
,即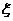 的分布列是
的分布列是
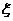 |
0 |
1 |
2 |
3 |
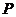 |
0.059 |
0.278 |
0. 435 |
0.226 |
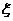 的期望是E
的期望是E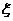 =0×0.059+1×0.278+2×0.435+3×0.226=1.826。
=0×0.059+1×0.278+2×0.435+3×0.226=1.826。
一校五题用题情况
|
学校 |
题量 |
学校 |
题量 |
学校 |
题量 |
|
基地 |
5 |
如东中学 |
5 |
南通中学 |
5 |
|
启东中学 |
6 |
栟茶中学 |
0 |
南通一中 |
2 |
|
海门中学 |
6 |
如皋中学 |
0 |
丰利中学 |
3 |
|
通州中学 |
5 |
海安中学 |
0 |
如皋一中 |
5 |
本资料由《七彩教育网》 提供!
41.(命题人:如东丰利中学花龙泉, 审题人:如东丰利中学朱兵)
已知向量 ,动点M到定直线
,动点M到定直线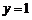 的距离等于
的距离等于 ,并且满足
,并且满足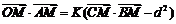 ,其中O为坐标原点,K为参数;
,其中O为坐标原点,K为参数;
(1)求动点M的轨迹方程,并判断曲线类型;
(2)当k= 时,求
时,求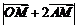 的最大值和最小值;
的最大值和最小值;
(3)在(2)的条件下,将曲线向左平移一个单位,在x轴上是否存在一点P(m,0)使得过点P的直线交该曲线于D、E两点、并且以DE为直径的圆经过原点,若存在,请求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
[解析](1)设 ,则由
,则由 ,
,
且O为原点得A(2,0),B(2,1),C(0,1)
从而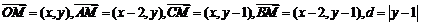
代入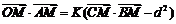 得
得
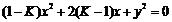 为所求轨迹方程
为所求轨迹方程
当K=1时, =0 轨迹为一条直线
=0 轨迹为一条直线
当K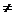 1时,
1时, ,若K=0,则为圆 ;若K
,若K=0,则为圆 ;若K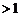 ,则为双曲线
,则为双曲线
(2)当K= 时,若
时,若 或
或 则为椭圆
则为椭圆
方程为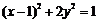 ,即
,即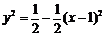 且
且
从而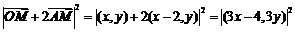
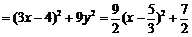
又 
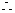 当
当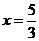 时,
时,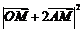 取最小值
取最小值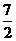 ,当
,当 时,
时,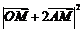 取最大值16
取最大值16
故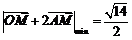 ,
,
(3)在(2)的条件下,将曲线向左平移一个单位后曲线方程为

假设存在过P(m,0)直线满足题意条件,不妨设过P(m,0)直线方程为
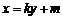
设D(x1,y1 ),E(x2,y2
),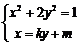 消去x得:
消去x得:
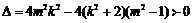 即
即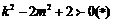
由韦达定理,得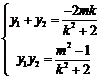
由于以DE为直径的圆都过原点则 ,即
,即

又因为

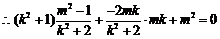 即
即 显然能满足
显然能满足
故当
40.(命题人:如东丰利中学宋浩,审题人:如东丰利中学袁峰)
下面的一组图形为某一四棱锥S-ABCD的侧面与底面。


(1)请画出四棱锥S-ABCD的示意图,是否存在一条侧棱SA垂直于底面ABCD?如果存在,请给出证明;
(2)若SA⊥面ABCD,点E为AB的中点,点G为SC的中点,求证EG∥面SAD.
(3)在(2)的条件下,求证:平面SEC⊥平面SCD;
[解析](1)存在一条侧棱垂直于底面(如右图)
证明:∵SA⊥AB,SA⊥AD,AB∩AD=A.
∴SA⊥面ABCD.
(2)取SD的中点F,连接GF,AF,则GF∥EA.
又∵GF=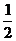 CD=
CD=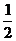 AB=AE,∴四边形ABCD为平行四边形,
AB=AE,∴四边形ABCD为平行四边形,
∴AF∥EG.
又∵EG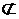 面SAD,AF
面SAD,AF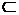 面SAD, ∴EG ∥面SAD.
面SAD, ∴EG ∥面SAD.
(3)∵△SAD为等腰三角形,F为SD的中点,∴AF⊥SD.
∵SA⊥面ABCD,∴SA⊥CD.
又∵AD⊥CD,∴CD⊥面SAD.
∵AF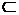 面SAD,∴CD⊥AF,∴AF⊥面SCD.
面SAD,∴CD⊥AF,∴AF⊥面SCD.
由(2)知,AF∥EG,所以EG⊥面SAD.
又∵EG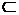 面SEC,∴面SEC⊥面SCD.
面SEC,∴面SEC⊥面SCD.
39.(命题人:南通一中吴勇贫,审题人:南通一中黄健)
已知曲线 的极坐标方程为
的极坐标方程为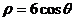 ,曲线
,曲线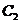 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 ,
,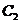 相交于
相交于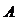 ,
, 两点.
两点.
(Ⅰ)把曲线 ,
,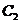 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦 的长度.
的长度.
解:(Ⅰ)曲线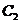 :
: (
(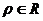 )表示直线
)表示直线 .曲线
.曲线 :
: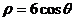 ,
,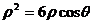 ,
,
所以 ,即
,即 .
.
(Ⅱ)圆心(3,0)到直线的距离
 ,
,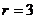 ,所以弦长
,所以弦长 =
=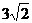 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com