
题目列表(包括答案和解析)
2.已知平面直角坐标系内的点A(1,1),B(2,4),C(-1,3),则向量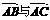 的夹角的余弦值为:
的夹角的余弦值为:
A. B.
B. C.
C. D.
D.
1.复数z=(m2+2m-3)+(m-1)i为纯虚数,则实数m的值为:
A.1 B.-1或3 C.-3或1 D.-3
22.(本小题满分15分)
解:(1) 依题意
依题意 在
在 时有解:即
时有解:即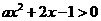 在
在 有解.则
有解.则 且方程
且方程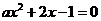 至少有一个正根.
至少有一个正根.
此时,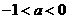 …………………………………………………………4分
…………………………………………………………4分
(2)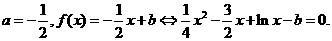
设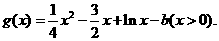 则
则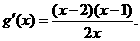 列表:
列表:
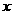 |
(0,1) |
1 |
(1,2) |
2 |
(2,4) |
 |
+ |
0 |
 |
0 |
+ |
 |
 |
极大值 |
 |
极小值 |
 |
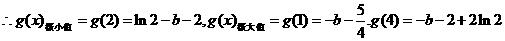 -----6分
-----6分
 方程
方程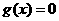 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则 解得:
解得: ……………………………………………5分
……………………………………………5分
(3)设 ,则
,则
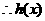 在
在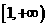 为减函数,且
为减函数,且 故当
故当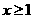 时有
时有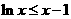 .
.
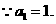 假设
假设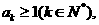 则
则 ,故
,故
从而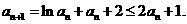

即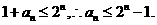 ……………………………………………5分
……………………………………………5分
本资料由《七彩教育网》 提供!
21. (本小题满分15分)
解:椭圆的顶点为(0,),即b=,
e==,所以a=2,2分
∴椭圆的标准方程为+=1 4分
(2) 不存在 .5分
(3)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(2)可得:|MN|=|x1-x2|=
==.
由消去y,并整理得x2=,
|AB|=|x3-x4|=4,11分
∴==4为定值. 5分
20.(本小题满分14分)
证(Ⅰ)因为 侧面
侧面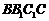 ,故
,故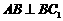
在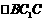 中,
中,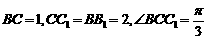 由余弦定理有
由余弦定理有

故有

而  且
且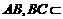 平面
平面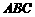

 ……………… 4分
……………… 4分
(Ⅱ)由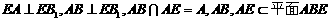
从而 且
且 故
故
不妨设  ,则
,则 ,则
,则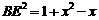
又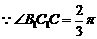 则
则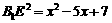
在 中有
中有
 从而
从而 (舍去)
(舍去)
故 为
为 的中点时,
的中点时, ……………… 5分
……………… 5分
(Ⅲ)取 的中点
的中点 ,
, 的中点
的中点 ,
, 的中点
的中点 ,
, 的中点
的中点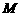
连 则
则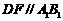 ,连
,连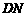 则
则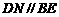 ,连
,连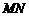 则
则
连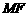 则
则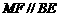 ,且
,且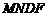 为矩形,
为矩形,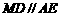
又 故
故 为所求二面角的平面角……………… 10分
为所求二面角的平面角……………… 10分
在 中,
中,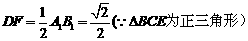

 ……………… 5分
……………… 5分
19. (本小题满分14分)
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件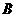 .由于事件
.由于事件 相互独立,且
相互独立,且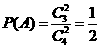 ,
, .
.
故取出的4个球均为黑球的概率为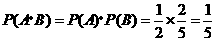 .(4分)
.(4分)
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件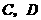 互斥,
互斥,
且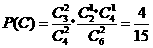 ,
, .
.
故取出的4个球中恰有1个红球的概率为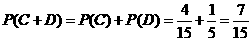 .(5分)
.(5分)
(Ⅲ)解: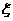 可能的取值为
可能的取值为 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得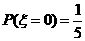 ,
,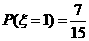 ,
,
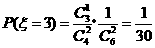 .从而
.从而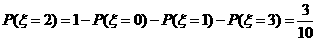 .
.
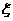 的分布列为
的分布列为
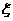 |
0 |
1 |
2 |
3 |
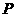 |
 |
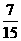 |
 |
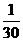 |
 的数学期望
的数学期望 .(5分)
.(5分)
18. (本小题满分14分)
答案:(1)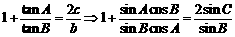 ,
,
即 ,
,
∴ ,∴
,∴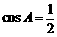 .
.
∵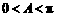 ,∴
,∴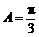 .(7分)
.(7分)
(2)m n
n  ,
,
 |mn|
|mn|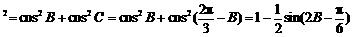 .
.
∵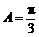 ,∴
,∴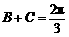 ,∴
,∴ .
.
从而 .
.
∴当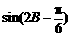 =1,即
=1,即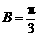 时,|m
时,|m n|
n| 取得最小值
取得最小值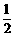 .
.
所以,|m n|
n|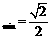 .(7分)
.(7分)
17. 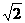 .
.
15.  16. -2
16. -2
11. 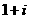 12.
-242
.
12.
-242
.
13 . (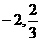 )
14.
)
14. 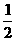 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com