
题目列表(包括答案和解析)
2.若函数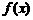 的反函数为
的反函数为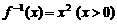 ,则
,则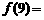 。
。
1.若复数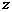 满足
满足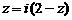 (
(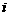 是虚数单位),则
是虚数单位),则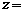 ____________。
____________。
23.必做题(本小题满分10分)
在四棱锥 中,
中,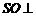 平面
平面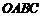 ,底面
,底面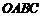 为正方形,且
为正方形,且 ,
,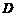 为
为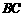 的中点,
的中点,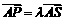 ,问是否存在
,问是否存在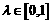 使
使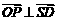 ?若存在,求出
?若存在,求出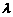 的值;若不存在,说明理由.
的值;若不存在,说明理由.
22.必做题(本小题满分10分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设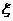 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且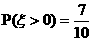 .
.
 (I) 求文娱队的人数;
(I) 求文娱队的人数;
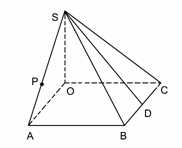
(II) 写出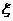 的概率分布列并计算
的概率分布列并计算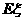 .
.
21. (选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
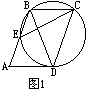
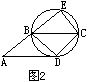 A.选修4-1∶几何证明选讲
A.选修4-1∶几何证明选讲
过平行四边形ABCD的顶点B、C、D的圆与直线AD相切,与直线AB相交于点E,已知AD=4,CE=5。
(1)如图1,若点E在线段AB上,求AE的长;
(2)点E能否在线段AB的延长线上?(即图2的情形是否存在?)若能,求出AE的长;若不能,请说明理由。
B.选修4-2:矩阵与变换
学校餐厅每天供应1000名学生用餐,每星期一有A、B两样菜可供选择,调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)若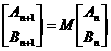 ,请你写出二阶矩阵M;
,请你写出二阶矩阵M;
(2)求二阶矩阵M的逆矩阵。
C.选修4-4 参数方程与极坐标
已知圆M的参数方程为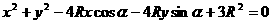 (R>0).
(R>0).
(1)求该圆的圆心的坐标以及圆M的半径。
(2)若题中条件R为定值,则当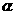 变化时,圆M都相切于一个定圆,试写出此圆的极坐标方程。
变化时,圆M都相切于一个定圆,试写出此圆的极坐标方程。
D.选修4-5:不等式选讲
已知函数 若函数
若函数 的图象在
的图象在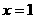 处的切线的斜率为0,且
处的切线的斜率为0,且 ,若
,若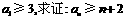
20.(本小题满分16分)
一小孩在某风景区玩耍,不慎将湖边一只救人的小船缆绳放开,小船被风刮跑,其方向与湖岸成 角(假设湖岸为直线),其中
角(假设湖岸为直线),其中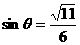 ,速度为2.5km/h;救生员及时发现,立即从同一地点开始追赶小船,已知救生员在水中游的速度为2 km/h,所以他只有先在岸上追赶一段时间后,再跳入水中追赶若干时间。
,速度为2.5km/h;救生员及时发现,立即从同一地点开始追赶小船,已知救生员在水中游的速度为2 km/h,所以他只有先在岸上追赶一段时间后,再跳入水中追赶若干时间。
(1)若救生员在岸上以6 km/h的速度追赶20分钟后,跳入水中追赶,试问他能否追上小船?如果能,则还需多少时间追上小船?如果不能,请说明理由。
(2)若救生员在岸上追赶的速度为6 km/h,考虑到他的体能情况,请你探索他选择何时跳入水中追赶,才能追上小船?
(3)若要使救生员能追上小船,试求他在岸上追赶的最小速度。(参考数据: ,精确到1)
,精确到1)
第Ⅱ卷(附加题 共40分)
附加题总分40分,时间用时30分钟.解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分16分)
在平面直角坐标系中,已知两点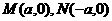 ,若某直线
,若某直线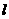 上有且只有一点
上有且只有一点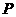 ,使
,使
 ,则称直线
,则称直线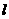 为“黄金直线”,点P为“黄金点”。
为“黄金直线”,点P为“黄金点”。
(1) 当 时,点
时,点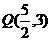 能否成为“黄金点”,若能,求出“黄金直线”方程;若不能,请说明理由。
能否成为“黄金点”,若能,求出“黄金直线”方程;若不能,请说明理由。
(2)当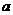 满足什么条件时, “黄金点” P的轨迹是圆?此时的“黄金直线”具有什么特征?
满足什么条件时, “黄金点” P的轨迹是圆?此时的“黄金直线”具有什么特征?
19(本小题满分16分)
(1)已知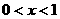 ,试求函数
,试求函数 的最小值;
的最小值;
(2)若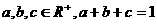 ,求证:(Ⅰ)
,求证:(Ⅰ)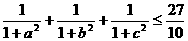 。
。
(Ⅱ)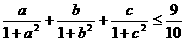
17. (本小题满分14分)
在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.
(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?
(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层,
(Ⅰ)共有几种不同的方案?
(Ⅱ)已知每根圆钢的直径为10cm,为考虑安全隐患,堆放高度不得高于4m,则选择哪个方案,最能节省堆放场地?
16.(本小题满分14分)
四棱锥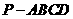 的底面与四个侧面的形状和大小如图所示。
的底面与四个侧面的形状和大小如图所示。

(I)试画出该四棱锥的直观图,并证明: E为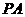 的中点时,
的中点时, 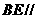 平面
平面 ;
;
(Ⅱ)若从该四棱锥的8条棱中,任取2条棱,则恰好满足相互垂直的概率是多少?
15. (本小题满分14分)
已知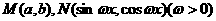 ,记
,记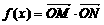 (O为坐标原点)。若
(O为坐标原点)。若 的最小正周期为2,并且当
的最小正周期为2,并且当 时,
时, 的最大值为5。
的最大值为5。
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)对任意的整数n,在区间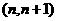 内是否存在曲线
内是否存在曲线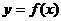 的对称轴?若存在,求出此对称轴方程;若不存在,说明理由。
的对称轴?若存在,求出此对称轴方程;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com