
题目列表(包括答案和解析)
1.已知集合 ,则
,则 (
)
(
)
A. B.
B. C.
C. D.
D.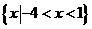
2.若复数 ,则实数
,则实数 的值为
(
)
的值为
(
)
A. B.
B. C.
C. D.
D.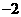
3.命题“ ,
, ”的否定为
( )
”的否定为
( )
A. ,
,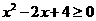 B.
B.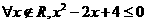
C. ,
,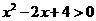 D.
D.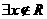 ,
,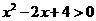
4.已知等差数列 中,
中,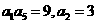 ,则
,则 ( )
( )
A. B.
B. C.
C. 或
或 D.
D. 或
或
5.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是 ( )
A . B.
B.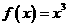 C.
C. D.
D.
6.设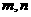 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题,其中为真命题的是
是两个不重合的平面,给定下列四个命题,其中为真命题的是
( )
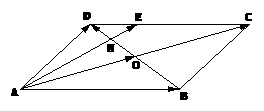 ①
①
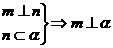 ②
② 
③  ④
④ 
A. ①和② B. ②和③ C. ③和④ D. ①和④
7.如上图,在平行四边形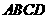 中,
中, 是对角线
是对角线 的交点,
的交点,  是线段
是线段 的中点,
的中点, 的延长线与
的延长线与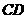 交于点
交于点 ,则下列说法错误的是
( )
,则下列说法错误的是
( )
A.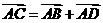 B.
B.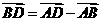 C.
C. D.
D.
8.在平面直角坐标系 中,已知
中,已知 的顶点
的顶点 和
和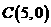 ,顶点
,顶点 在双曲线
在双曲线 上,则
上,则 为
( )
为
( )
A.  B.
B.
 C.
C.
 D.
D.

9.对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做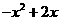 的“上确界”,若
的“上确界”,若 ,且
,且 则
则 的“上确界”为
(
)
的“上确界”为
(
)
A.  B.
B.
 C.
C.
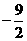 D.
D.

10. 将
将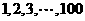 这
这 个自然数任意分成
个自然数任意分成 组,每组两个数,现将每组的两个数中任意一个记为
组,每组两个数,现将每组的两个数中任意一个记为 ,另一个数记为
,另一个数记为 ,按框图所示进行运算(注:框图中每次“输入
,按框图所示进行运算(注:框图中每次“输入 ”为同一组的
”为同一组的 值,且每组数据不重复输入),则输出的
值,且每组数据不重复输入),则输出的 最大值为 ( )
最大值为 ( )
A. B.
B. C.
C. D.
D.
第Ⅱ卷(填空题、解答题 共100分)
二。填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
21、(本小题满分14分)
在R上定义运算◎: ◎
◎ =
=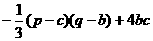 (
(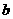 、
、 为实常数)。记
为实常数)。记 ,
, ,
,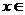 R,令
R,令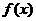 =
= ◎
◎ 。
。
(1) 如果函数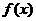 在
在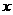 =1处有极值
=1处有极值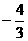 ,试确定
,试确定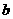 、
、 的值;
的值;
(2)
求曲线 =
=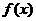 上斜率为
上斜率为 的切线与该曲线的公共点;
的切线与该曲线的公共点;
(3)
记 (-1≤
(-1≤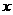 ≤1)的最大值为M,若M≥
≤1)的最大值为M,若M≥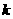 对任意的
对任意的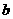 、
、 恒成立,试求
恒成立,试求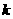 的最大值。
的最大值。
20、(本小题满分12分)

 A、B两城相距30km,现计划在两城外以 AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城A的影响度与厂址到城A的距离的平方成反比(比例系数
A、B两城相距30km,现计划在两城外以 AB为直径的半圆弧AB上选择一点C建造垃圾处理厂,其对城A的影响度与厂址到城A的距离的平方成反比(比例系数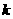 为正数),对城B的影响度也与厂址到城B的距离的平方成反比,且当厂址在弧AB的中点时,对城B的影响度是对城A的影响度的四倍,
为正数),对城B的影响度也与厂址到城B的距离的平方成反比,且当厂址在弧AB的中点时,对城B的影响度是对城A的影响度的四倍,
(1)试将总影响度 (对两城的影响度之和)表示成厂址到城A的距离
(对两城的影响度之和)表示成厂址到城A的距离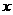 的函数;
的函数;
(2)是否存在一点,使建在此处的垃圾处理厂对两城的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
19、(本小题满分14分)
已知函数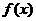 =
= 的单调递减区间是(-1,3),且在
的单调递减区间是(-1,3),且在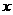 =1处的切线方程为:
=1处的切线方程为:
(1)、求函数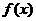 的解析式;
的解析式;
(2)、求函数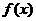 在区间[-4,4 ]上的最值;
在区间[-4,4 ]上的最值;
(3)、若过点(0,m)有且只有一条直线与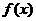 相切,求m的取值范围。
相切,求m的取值范围。
18、(本小题满分10分)
已知命题p:关于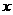 的方程
的方程 有负根 ;
命题q:不等式
有负根 ;
命题q:不等式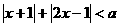 的解集为
的解集为 。且“p∨q”是真命题,“p∧q”是假命题,求实数
。且“p∨q”是真命题,“p∧q”是假命题,求实数 的取值范围。
的取值范围。
17、(本小题满分13分)
定义在(0,+∞)上的函数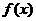 满足:对任意的
满足:对任意的 (0,+∞),都有
(0,+∞),都有 ,且当0<
,且当0<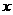 <1时, 都有
<1时, 都有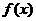 >1成立。
>1成立。
(1)、判断并证明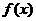 在定义域(0,+∞)上的单调性;
在定义域(0,+∞)上的单调性;
(2)、若 7,解不等式:
7,解不等式: >4
>4
16、(本小题满分12分)
已知函数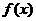 =
=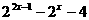 ,
,
(1)求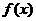 的零点;
的零点;
(2)求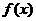 的值域。
的值域。
15、一辆汽车从静止状态开始启动前进,随即因故减速停车,其加速度 是时间
是时间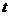 的函数:
的函数: (单位:米/秒2),则该车从启动到停下来共前进了
米。
(单位:米/秒2),则该车从启动到停下来共前进了
米。
14、已知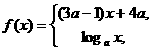
 是R上的减函数,那么
是R上的减函数,那么 的取值范围是
。
的取值范围是
。
13、已知定义域为D的函数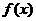 ,对任意
,对任意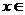 D,存在正数K,都有
D,存在正数K,都有 ≤K成立,则称函数
≤K成立,则称函数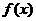 是定义域D上的“有界函数”,已知下列函数:①
是定义域D上的“有界函数”,已知下列函数:①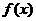 =
= ②
②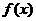 =
= ③
③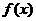 =
= ④
④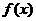 =
= 其中是“有界函数”的是 (写出所有满足要求的函数的序号)。
其中是“有界函数”的是 (写出所有满足要求的函数的序号)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com