
题目列表(包括答案和解析)
高考立体几何试题一般共有4道(选择、填空题3道, 解答题1道), 共计总分27分左右,考查的知识点在20个以内。随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展,从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题。
预测2010年高考试题:
(1)单独求夹角和距离的题目多为选择题、填空题,分值大约5分左右;解答题中的分步设问中一定有求夹角、距离的问题,分值为6分左右;
(2)选择、填空题考核立几中的计算型问题, 而解答题着重考查立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提
3.掌握平行平面间的距离,会求二面角及其平面角;
2.掌握点、直线到平面的距离,直线和平面所成的角;
1.掌握两条直线所成的角和距离的概念及等角定理;(对于异面直线的距离,只要求会计算已给出公垂线时的距离)。
5.证明两平面平行的方法:
(1)利用定义证明。利用反证法,假设两平面不平行,则它们必相交,再导出矛盾。
(2)判定定理:一个平面内有两条相交直线都平行于另一个平面,则这两个平面平行,这个定理可简记为线面平行则面面平行。用符号表示是:a∩b,a 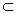 α,b
α,b 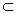 α,a∥β,b∥β,则α∥β。
α,a∥β,b∥β,则α∥β。
(3)垂直于同一直线的两个平面平行。用符号表示是:a⊥α,a⊥β则α∥β。
(4)平行于同一个平面的两个平面平行。
两个平面平行的性质有五条:
(1)两个平面平行,其中一个平面内的任一直线必平行于另一个平面,这个定理可简记为:“面面平行,则线面平行”。用符号表示是:α∥β,a 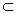 α,则a∥β。
α,则a∥β。
(2)如果两个平行平面同时与第三个平面相交,那么它们的交线平行,这个定理可简记为:“面面平行,则线线平行”。用符号表示是:α∥β,α∩γ=a,β∩γ=b,则a∥b。
(3)一条直线垂直于两平行平面中的一个平面,它也垂直于另一个平面。这个定理可用于证线面垂直。用符号表示是:α∥β,a⊥α,则a⊥β。
(4)夹在两个平行平面间的平行线段相等
(5)过平面外一点只有一个平面与已知平面平行
4.直线和平面相互平行
证明方法:1证明直线和这个平面内的一条直线相互平行;2证明这条直线的方向量和这个平面内的一个向量相互平行;3证明这条直线的方向量和这个平面的法向量相互垂直。
3.注意下面的转化关系:

2.注意立体几何问题向平面几何问题的转化,即立几问题平面化
在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上,研究有关平行的判定依据(定义、公理和定理)、判定方法及有关性质的应用;在有关问题的解决过程中,进一步了解和掌握相关公理、定理的内容和功能,并探索立体几何中论证问题的规律;在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用.
1.用类比的思想去认识面的垂直与平行关系,注意垂直与平行间的联系。
题型1:共线、共点和共面问题
例1.(1)如图所示,平面ABD 平面BCD =直线BD ,M 、N 、P 、Q 分别为线段AB 、BC 、CD 、DA 上的点,四边形MNPQ 是以PN 、QM 为腰的梯形。
平面BCD =直线BD ,M 、N 、P 、Q 分别为线段AB 、BC 、CD 、DA 上的点,四边形MNPQ 是以PN 、QM 为腰的梯形。
试证明三直线BD 、MQ 、NP 共点。
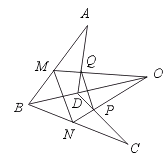
证明:∵ 四边形MNPQ 是梯形,且MQ 、NP 是腰,
∴直线MQ 、NP 必相交于某一点O 。
∵ O 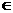 直线MQ ;直线MQ
直线MQ ;直线MQ 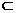 平面ABD ,
平面ABD ,
∴ O 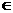 平面ABD。
平面ABD。
同理,O 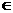 平面BCD ,又两平面ABD 、BCD 的交线为BD ,
平面BCD ,又两平面ABD 、BCD 的交线为BD ,
故由公理二知,O 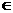 直线BD ,从而三直线BD 、MQ 、NP 共点。
直线BD ,从而三直线BD 、MQ 、NP 共点。
点评:由已知条件,直线MQ 、NP 必相交于一点O ,因此,问题转化为求证点O 在直线BD 上,由公理二,就是要寻找两个平面,使直线BD 是这两个平面的交线,同时点O 是这两个平面的公共点即可.“三点共线”及“三线共点”的问题都可以转化为证明“点在直线上”的问题。
 (2)如图所示,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线
(2)如图所示,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC分别与平面α相交于点E,G,H,F.求证:E,F,G,H四点必定共线
证明:∵AB∥CD,
∴AB,CD确定一个平面β.
又∵AB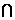 α=E,AB
α=E,AB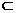 β,∴E∈α,E∈β,
β,∴E∈α,E∈β,
即E为平面α与β的一个公共点。
同理可证F,G,H均为平面α与β的公共点.
∵两个平面有公共点,它们有且只有一条通过公共点的公共直线,
∴E,F,G,H四点必定共线。
点评:在立体几何的问题中,证明若干点共线时,常运用公理2,即先证明这些点都是某二平面的公共点,而后得出这些点都在二平面的交线上的结论。
例2.已知:a,b,c,d是不共点且两两相交的四条直线,求证:a,b,c,d共面。
证明:1o若当四条直线中有三条相交于一点,不妨设a,b,c相交于一点A,
但AÏd,如图1所示:
∴直线d和A确定一个平面α。
 又设直线d与a,b,c分别相交于E,F,G,
又设直线d与a,b,c分别相交于E,F,G,
则A,E,F,G∈α。
∵A,E∈α,A,E∈a,∴a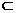 α。
α。
同理可证b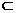 α,c
α,c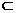 α。
α。
∴a,b,c,d在同一平面α内。
2o当四条直线中任何三条都不共点时,
如图2所示:
∵这四条直线两两相交,则设相交直线a,b确定一个平面α。
设直线c与a,b分别交于点H,K,则H,K∈α。
又 H,K∈c,∴c,则c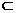 α。
α。
同理可证d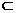 α。
α。
∴a,b,c,d四条直线在同一平面α内.
点评:证明若干条线(或若干个点)共面的一般步骤是:首先根据公理3或推论,由题给条件中的部分线(或点)确定一个平面,然后再根据公理1证明其余的线(或点)均在这个平面内。本题最容易忽视“三线共点”这一种情况。因此,在分析题意时,应仔细推敲问题中每一句话的含义。
题型2:异面直线的判定与应用
例3.已知:如图所示,a  b =a ,b
b =a ,b 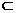 b ,a
b ,a  b =A ,c
b =A ,c 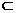 a ,c ∥a 。求证直线b 、c 为异面直线
a ,c ∥a 。求证直线b 、c 为异面直线

证法一:假设b 、c 共面于g .由A 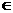 a ,a ∥c 知,A
a ,a ∥c 知,A  c ,而a
c ,而a  b =A,a
b =A,a  b =a ,
b =a ,
∴ A
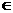 g ,A
g ,A 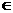 a。
a。
又c 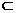 a ,∴ g 、a 都经过直线c 及其外的一点A,
a ,∴ g 、a 都经过直线c 及其外的一点A,
∴ g 与a 重合,于是a 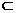 g ,又b
g ,又b 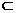 b。
b。
又g 、b 都经过两相交直线a 、b ,从而g 、b 重合。
∴ a 、b 、g 为同一平面,这与a  b =a 矛盾
b =a 矛盾
∴ b 、c 为异面直线.
证法二:假设b 、c 共面,则b ,c 相交或平行。
(1)若b ∥c ,又a ∥c ,则由公理4知a ∥b ,这与a  b =A 矛盾。
b =A 矛盾。
(2)若b  c =P ,已知b
c =P ,已知b 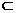 b ,c
b ,c 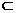 a ,则P 是a 、b 的公共点,由公理2,P
a ,则P 是a 、b 的公共点,由公理2,P 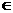 a ,又b
a ,又b  c =P ,即P
c =P ,即P 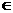 c ,故a
c ,故a  c =P ,这与a ∥c 矛盾
c =P ,这与a ∥c 矛盾
综合(1)、(2)可知,b 、c 为异面直线。
证法三:∵ a  b =a ,a
b =a ,a  b =A ,∴ A
b =A ,∴ A
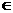 a 。
a 。
∵ a
∥c ,∴ A
 c ,
c ,
在直线b 上任取一点P(P 异于A),则P  a(否则b
a(否则b 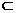 a ,又a
a ,又a 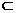 a ,则a 、b 都经过两相交直线a 、b ,则a 、b 重合,与a
a ,则a 、b 都经过两相交直线a 、b ,则a 、b 重合,与a  b =a 矛盾)。
b =a 矛盾)。
又c 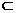 a ,于是根据“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线”知,b 、c 为异面直线。
a ,于是根据“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线”知,b 、c 为异面直线。
点评:证明两直线为异面直线的思路主要有两条:一是利用反证法;二是利用结论“过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.。异面直线又有两条途径:其一是直接假设b 、c 共面而产生矛盾;其二是假设b 、c 平行与相交;分别产生矛盾。判定直线异面,若为解答题,则用得最多的是证法一、二的思路;若为选择或填空题,则往往都是用证法三的思路。用反证法证题,一般可归纳为四个步骤:(1)否定结论;(2)进行推理;(3)导出矛盾;(4)肯定结论.
宜用反证法证明的命题往往是(1)基本定理或某一知识系统的初始阶段的命题(如立体几何中的线面、面面平行的判定定量的证明等);(2)肯定或否定型的命题(如结论中出现“必有”、“必不存在”等一类命题);(3)唯一型的命题(如“图形唯一”、“方程解唯一”等一类命题);(4)正面情况较为繁多,而结论的反面却只有一两种情况的一类命题;(5)结论中出现“至多”、“不多于”等一类命题。
例4.(1)已知异面直线a,b所成的角为70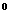 ,则过空间一定点O,与两条异面直线a,b都成60
,则过空间一定点O,与两条异面直线a,b都成60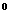 角的直线有( )条
角的直线有( )条
A.1 B.2 C.3 D.4
(2)异面直线a,b所成的角为 ,空间中有一定点O,过点O有3条直线与a,b所成角都是60
,空间中有一定点O,过点O有3条直线与a,b所成角都是60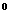 ,则
,则 的取值可能是( )
的取值可能是( )
A.30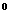 B.50
B.50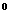 C.60
C.60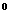 D.90
D.90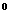
解析:(1)过空间一点O分别作 ∥a,
∥a,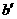 ∥b。
∥b。
将两对对顶角的平分线绕O点分别在竖直平面内转动,总能得到与 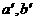 都成60
都成60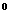 角的直线。故过点 O与a,b都成60
角的直线。故过点 O与a,b都成60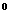 角的直线有4条,从而选D。
角的直线有4条,从而选D。
(2)过点O分别作 ∥a、
∥a、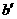 ∥b,则过点O有三条直线与a,b所成角都为60
∥b,则过点O有三条直线与a,b所成角都为60 ,等价于过点O有三条直线与
,等价于过点O有三条直线与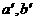 所成角都为60
所成角都为60 ,其中一条正是
,其中一条正是 角的平分线。从而可得选项为C。
角的平分线。从而可得选项为C。
点评:该题以学生对异面直线所成的角会适当转化,较好的考察了空间想象能力
题型3:线线平行的判定与性质
例5.(2009江苏卷)设 和
和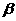 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于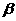 内的两条直线,则
内的两条直线,则 平行于
平行于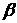 ;
;
(2)若 外一条直线
外一条直线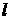 与
与 内的一条直线平行,则
内的一条直线平行,则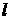 和
和 平行;
平行;
(3)设 和
和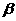 相交于直线
相交于直线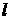 ,若
,若 内有一条直线垂直于
内有一条直线垂直于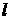 ,则
,则 和
和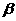 垂直;
垂直;
(4)直线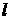 与
与 垂直的充分必要条件是
垂直的充分必要条件是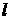 与
与 内的两条直线垂直。
内的两条直线垂直。
上面命题中,真命题的序号 (写出所有真命题的序号).
[解析] 考查立体几何中的直线、平面的垂直与平行判定的相关定理。
真命题的序号是(1)(2)
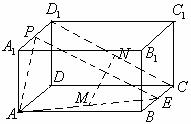
例6.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE。
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB。
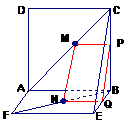 ∴MP∥NQ,又AM=NF,AC=BF,
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE。
证法二:如图过M作MH⊥AB于H,则MH∥BC,
 ∴
∴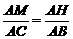
连结NH,由BF=AC,FN=AM,得
∴ NH//AF//BE
由MH//BC, NH//BE得:平面MNH//平面BCE
 ∴MN∥平面BCE。
∴MN∥平面BCE。
题型4:线面平行的判定与性质
例7.(2009山东卷理)(本小题满分12分)
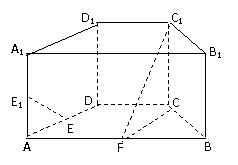 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA =2, E、E
=2, E、E 、F分别是棱AD、AA
、F分别是棱AD、AA 、AB的中点。
、AB的中点。
(1)
证明:直线EE //平面FCC
//平面FCC ;
;
(2)
求二面角B-FC -C的余弦值
-C的余弦值
 解法一:(1)在直四棱柱ABCD-A
解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为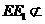 平面FCC
平面FCC ,
,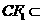 平面FCC
平面FCC ,
,
所以直线EE //平面FCC
//平面FCC .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,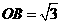 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵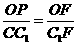 ∴
∴ ,
,
在Rt△OPF中, ,
,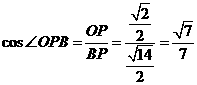 ,所以二面角B-FC
,所以二面角B-FC -C的余弦值为
-C的余弦值为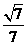 .
.
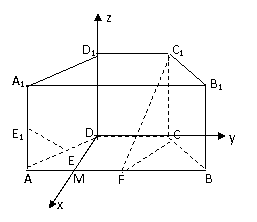 解法二:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
解法二:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
,则D(0,0,0),A(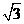 ,-1,0),F(
,-1,0),F(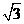 ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E( ,
, ,0),E1(
,0),E1(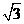 ,-1,1),所以
,-1,1),所以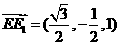 ,
,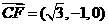 ,
,
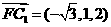 设平面CC1F的法向量为
设平面CC1F的法向量为 则
则 所以
所以 取
取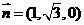 ,则
,则 ,所以
,所以 ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
.
(2) ,设平面BFC1的法向量为
,设平面BFC1的法向量为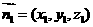 ,则
,则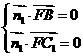 所以
所以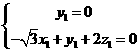 ,取
,取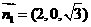 ,则
,则 ,
,
 ,
, ,
,
所以 ,由图可知二面角B-FC
,由图可知二面角B-FC -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC -C的余弦值为
-C的余弦值为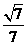 .
.
[命题立意]:本题主要考查直棱柱的概念、线面位置关系的判定和二面角的计算.考查空间想象能力和推理运算能力,以及应用向量知识解答问题的能力.
例8.(2008四川 19,理21)
(本小题满分12分)
如图,平面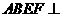 平面
平面 ,四边形
,四边形 与
与 都是直角梯形,
都是直角梯形, ,
, ∥
∥ ,
, ∥
∥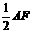 .
.
(Ⅰ)证明: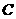 、
、 、
、 、
、 四点共面;
四点共面;
(Ⅱ)设 ,求二面角
,求二面角 的大小.
的大小.


解析:不是会不会的问题,而是熟不熟的问题,答题时间是最大问题.
(Ⅰ)∵面 面
面 ,
,
∴ 面
面 .
.
∴以 为原点,以
为原点,以 ,
, ,
, 所在直线为
所在直线为 轴,
轴, 轴,
轴, 轴,
轴,
建立如图所示的空间直角坐标系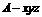 .
.
不妨设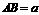 ,
,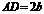 ,
,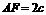 ,则
,则
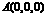 ,
,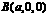 ,
,
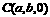 ,
,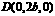 ,
,
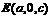 ,
,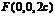 .
.
∴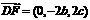 ,
,
 ,
,
∴ ,
,
∴ ,
,
∵ ,∴
,∴ ,∴C、D、E、F四点共面.
,∴C、D、E、F四点共面.
(Ⅱ)设 ,则
,则 ,
,
∴ ,
,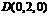 ,
, .
.
设平面 的法向量为
的法向量为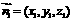 ,
,
由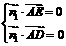 ,得
,得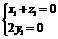 ,
,
设平面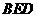 的法向量为
的法向量为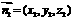
由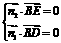 ,得
,得 ,
,
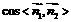

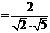

由图知,二面角 为锐角,
为锐角,
∴其大小为 .
.
点评:证共面就是证平行,求二面角转为求法向量夹角,时间问题是本题的困惑处.心浮气燥会在计算、书写、时间上丢分.因建系容易,提倡用向量法.本时耗时要超过17题与18题用时之和.
题型5:面面平行的判定与性质
例9.如图,正方体ABCD-A1B1C1D1 的棱长为a。证明:平面ACD1 ∥平面A1C1B 。
证明:如图,∵ A1BCD1 是矩形,A1B ∥D1C 。
又D1C 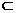 平面D1CA ,A1B
平面D1CA ,A1B  平面D1CA ,
平面D1CA ,
∴ A1B ∥平面D1CA。
同理A1C1 ∥平面D1CA ,又A1C1  A1B =A1 ,∴ 平面D1CA ∥平面BA1C1 .
A1B =A1 ,∴ 平面D1CA ∥平面BA1C1 .
点评:证明面面平行,关键在于证明A1C1 与A1B 两相交直线分别与平面ACD1 平行。
 例10.P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PCA、△PAB的重心。
例10.P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PCA、△PAB的重心。
(1)求证:平面A′B′C′∥平面ABC;
(2)S△A′B′C′∶S△ABC的值。
解析:(1)取AB、BC的中点M、N,
则
∴A′C′∥MN?A′C′∥平面ABC。
同理A′B′∥面ABC,
∴△A′B′C′∥面ABC.
(2)
 A′C′=
A′C′= MN=
MN= ·
·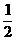 AC=
AC= AC
AC
 ,
,
同理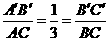
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com