
题目列表(包括答案和解析)
3、已知函数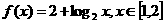 ,则函数
,则函数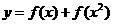 的值域为( )
的值域为( )
A.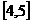 B.
B.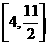 C.
C.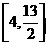 D.
D.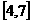
2、如果一个点是一个指数函数和一个对数函数的图像的交点,那么称这个点为"好点".下列四个点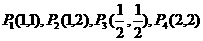 中,"好点"有( )个
中,"好点"有( )个
A. 1 B.2 C.3 D.4
1、设a=0.3 ,b=2
,b=2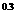 ,c=log
,c=log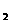
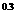 则它们的大小关系为( )
则它们的大小关系为( )
A.c<a<b B.a<c<b C.a<b<c D.b<c<a
12、解:(Ⅰ) ∵
 ,
∴
,
∴ 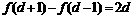 .
即
.
即  ,
解得 d =2.
,
解得 d =2.
∴ 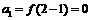 . ∴
. ∴ 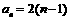 .
………………………………… 2分
.
………………………………… 2分
∵ 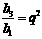 ,
∴
,
∴ 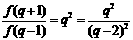 . ∵
. ∵ 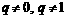 , ∴
, ∴  .
.
又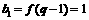 ,
∴
,
∴ 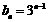 .…………………………………………
4分
.…………………………………………
4分
(Ⅱ) 由题设知 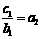 ,
∴
,
∴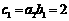 .
.
当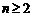 时,
时, 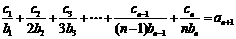 ,
,  ,
,
两式相减,得 .
.
∴ 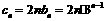 (
( 适合).…………………………… 7分
适合).…………………………… 7分
设T=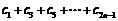 ,
,
∴ 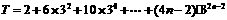
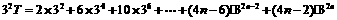
两式相减 ,得
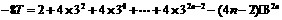

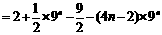
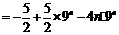 .
.
∴
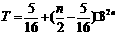 .…………………………………………………
9分
.…………………………………………………
9分
(Ⅲ) 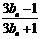
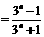
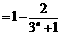 ,
, 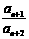
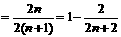 .
.
现只须比较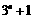 与
与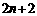 的大小.
的大小.
当n=1时, 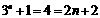 ;
;
当n=2时, 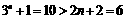 ;
;
当n=3时, 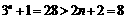 ;
;
当n=4时, 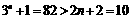 .
.
猜想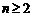 时,
时,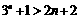 .
.
用数学归纳法证明
(1)当n=2时,左边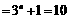 ,右边
,右边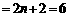 ,
,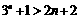 成立.
成立.
(2)假设当n=k时, 不等式成立,即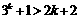 .
.
当n=k+1时, 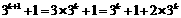

 .
.
即当n=k+1时,不等式也成立.
由(1)(2),可知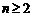 时,
时,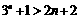 都成立.
都成立.
所以
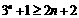 (当且仅当n=1时,等号成立)
(当且仅当n=1时,等号成立)
所以
 .即
.即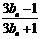
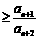 .
…………………………… 14分
.
…………………………… 14分
11、解:(I)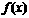 是二次函数,且
是二次函数,且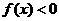 的解集是
的解集是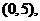
 可设
可设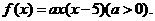
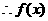 在区间
在区间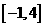 上的最大值是
上的最大值是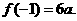
由已知,得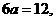
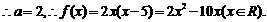
(II)方程 等价于方程
等价于方程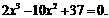
设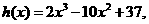 则
则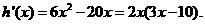
当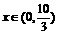 时,
时,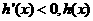 是减函数;当
是减函数;当 时,
时,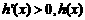 是增函数。
是增函数。 
 方程
方程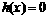 在区间
在区间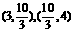 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间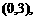
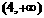 内没有实数根,所以存在惟一的自然数
内没有实数根,所以存在惟一的自然数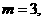 使得方程
使得方程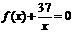 在区间
在区间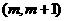 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。
0、解:(Ⅰ)设需要新建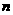 个桥墩,
个桥墩,
所以 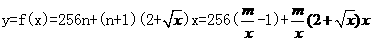
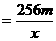
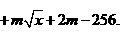
(Ⅱ) 由(Ⅰ)知,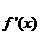
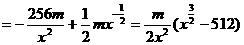
令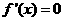 ,得
,得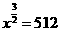 ,所以
,所以 =64
=64
当0< <64时
<64时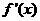 <0,
<0,
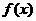 在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当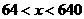 时,
时,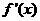 >0.
>0. 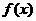 在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以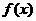 在
在 =64处取得最小值,此时,
=64处取得最小值,此时,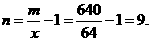
故需新建9个桥墩才能使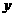 最小。
最小。
9、解:(Ⅰ)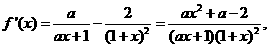
∵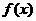 在x=1处取得极值,∴
在x=1处取得极值,∴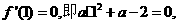 解得
解得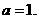
(Ⅱ)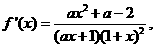 ∵
∵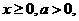 ∴
∴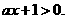
①当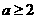 时,在区间
时,在区间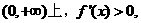 ∴
∴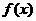 的单调增区间为
的单调增区间为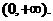
②当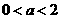 时,由
时,由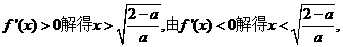
∴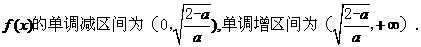
(Ⅲ)当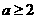 时,由(Ⅱ)①知,
时,由(Ⅱ)①知,
当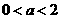 时,由(Ⅱ)②知,
时,由(Ⅱ)②知, 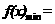
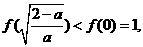 矛盾。
矛盾。
综上可知,若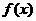 得最小值为1,则a的取值范围是
得最小值为1,则a的取值范围是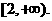
8、
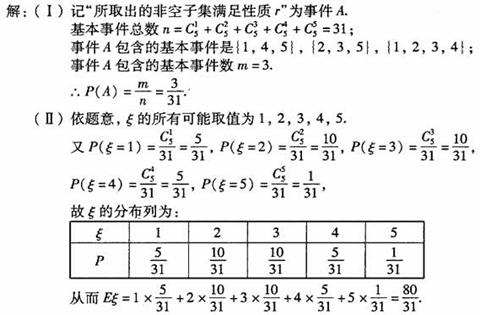
7、 解:由P知,a=0或
解:由P知,a=0或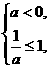 解得a≤0.
解得a≤0.
由Q知,Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
“﹁P或Q”为真,“﹁P且Q”为假,∴P与Q一真一假;
若P正确,Q不正确,则有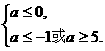 ∴a≤-1.
∴a≤-1.
若P不正确,Q正确,则有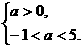 ∴0<a<5. 综上可知,a的取值范围为a≤-1或0<a<5.
∴0<a<5. 综上可知,a的取值范围为a≤-1或0<a<5.
6.(1)∵f’(x)=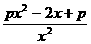 ,要使f(x)为单调增函数,须f’(x)≥0恒成立,即px2-2x+p≥0恒成立,即p≥
,要使f(x)为单调增函数,须f’(x)≥0恒成立,即px2-2x+p≥0恒成立,即p≥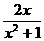 =
=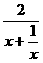 恒成立,又
恒成立,又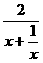 ≤1,
≤1,
所以当p≥1时,f(x)在(0,+∞)为单调增函数。
要使f(x)为单调减函数,须f’(x) ≤0恒成立,
即px2-2x+0≤0恒成立,即p≤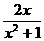 =
=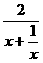 恒成立,又
恒成立,又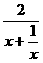 >0,
>0,
所以当p≤0时,f(x)在(0,+ ∞)为单调减函数。
综上所述,f(x)在(0,+∞)为单调函数,p的取值范围为p≥1或p≤0…(4分)
(2)∵f’(x)=p+ ,∴f’(1)=2(p-1),设直线l:y=2(p-1)(x-1),
,∴f’(1)=2(p-1),设直线l:y=2(p-1)(x-1),
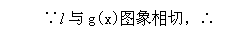 y=2(p-1)(x-1)
y=2(p-1)(x-1)
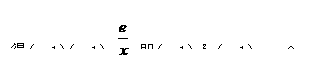 y=
y=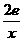
当p=1时,方程无解;当p≠1时由△=(p-1)2-4(p-1)(-e)=0,
得p=1-4e,综上,p=1-4e……………………………………………………(4分)
(3)因g(x)=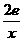 在[1,e]上为减函数,所以g(x)∈[2,2e]
在[1,e]上为减函数,所以g(x)∈[2,2e]
①当p≤0时,由(1)知f(x)在[1,e]上递减 f(x)max=f(1)=0<2,不合题意
f(x)max=f(1)=0<2,不合题意
②当p≥1时,由(1)知f(x)在[1,e]上递增,f(1) <2,又g(x)在[1,e]上为减函数,故只需f(x)max>g(x)min,x∈[1,e],
即:f(e)=p(e-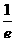 )-2lne>2
)-2lne>2 p>
p>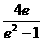 .
.
③当0<p<1时,因x-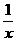 ≥0,x∈[1,e]
≥0,x∈[1,e]
所以f(x)=p(x-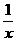 )-2lnx≤(x-
)-2lnx≤(x-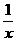 )-2lnx≤e-
)-2lnx≤e-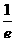 -2lne<2不合题意
-2lne<2不合题意
综上,p的取值范围为(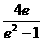 ,+∞)……………………………………(5分)
,+∞)……………………………………(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com