题型1：输入、输出和赋值语句

例1．判断下列给出的输入语句、输出语句和赋值语句是否正确？为什么？

(1)输入语句 INPUT　 a；b；c

(2)输出语句 A＝4

(3)赋值语句 3＝B

(4)赋值语句　 A＝B＝－2

解析：(1)错，变量之间应用“，”号隔开；

(2)错，PRINT语句不能用赋值号“=”；

(3)错，赋值语句中“=”号左右不能互换；

(4)错，一个赋值语句只能给一个变量赋值

点评：输入语句、输出语句和赋值语句基本上对应于算法中的顺序结构。输入语句、输出语句和赋值语句都不包括“控制转移”，由它们组成的程序段必然是顺序结构

(5)4、(2009年广东卷文)某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：

队员i	1	2	3	4	5	6
三分球个数

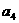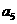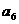下图(右)是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填　　　 　，输出的s=　　　

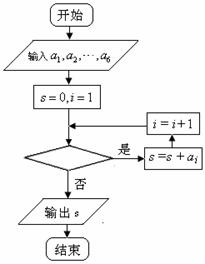(注：框图中的赋值符号“=”也可以写成“←”或“：=”)

[解析]顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，所图中判断框应填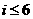，输出的s=.

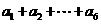答案　 ,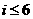

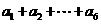
例2．请写出下面运算输出的结果。

(1)

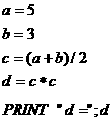
(2)

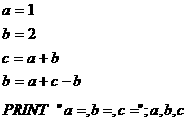
(3)

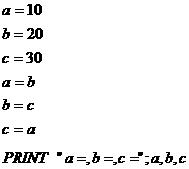
解析：

(1)16；语句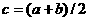是将a，b和的一半赋值给变量c，语句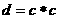是将c的平方赋值给d，最后输出d的值

(2)1，2，3；语句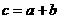是将a，b的和赋值给c，语句是将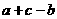的值赋值给了b。

(3)20，30，20；经过语句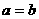后a，b，c的值是20，20，30。经过语句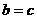后a，b，c的值是20，30，30。经过语句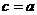后a，b，c的值是20，30，20。

点评：语句的识别问题是一个逆向性思维，一般我们认为我们的学习是从算法步骤(自然语言)至程序框图，再到算法语言(程序)。如果将程序摆在我们的面前时，我们要从识别逐个语句，整体把握，概括程序的功能

题型2：赋值语句的应用

例3．写出求三个数a，b，c的方差的程序。

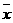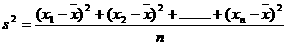解析：方差是在初中统计内容中学习过的知识，计算所有数的方差首先计算所有数的平均数，通过公式来计算。

算法步骤：

第一步：计算平均数；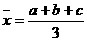

第二步：计算方差；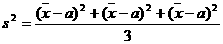

第三步：得到的结果即为所求。

程序如下：

INPUT a，b，c

y=(a+b+c)/3

S=((a－y)²+ (b－y)²+ (c－y)²)/3

PRINT S

END

点评：套用公式求值问题是传统数学求值问题的一种，它是一种典型的顺序结构，也就是说只通过输入、输出和赋值语句就可以完成任务。解决这类问题的关键是先分析这种问题的解法，即构造计算的过程，再写出算法步骤和流程图，再翻译成算法语句即可

例4．编写一个程序，要求输入的两个正数a和b的值，输出a^b和b^a的值。

解析：可以利用INPUT语句输入两个正数，然后将a^b和b^a的值分别赋给两个变量输出即可。也可以将a^b和b^a的底数和幂数进行交换，故还可以利用赋值语句，采用将两个变量的值互换的办法实现。

程序1：

INPUT “a，b：”；a，b

A=a^b

B=b^a

PRINT “a^b=”；A，“b^a=”；B

END

程序2：

INPUT “a，b：”；a，b

A=a^b

PRINT “a^b=”；A

x=a

a=b

b=x

A=a^b

PRINT “a^b=”；A

END

点评：交换a，b的值可通过下面三个语句来实现：

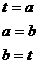
通过引进一个变量t实现变量a和b的值的交换，因此只需用赋值语句即可实现算法。在一些较为复杂的问题算法中经常需要对两个变量的值进行交换，因此应熟练掌握这种方法。

题型3：条件语句

例5．编写程序，输出两个不相等的实数a、b的最大值

解析：要输出两个不相等的实数a、b的最大值，从而想到对a，b的大小关系进行判断，a，b的大小关系有两种情况：(1)a>b；(2)b>a，这也就用到了我们经常提及的分类讨论的方式，找出两个数的最大值

解：算法一：

第一步：输入a， b的数值；

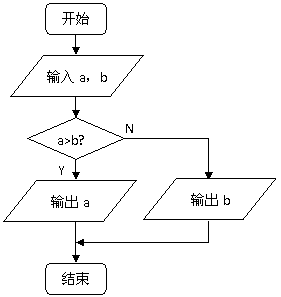第二步：判断a，b的大小关系，若a>b，则输出a的值，否则输出b的值。

(程序框图如右图)

程序如下：(“IF-THEN-ELSE”语句)

INPUT“a，b”；a，b

IF　 a＞b　 THEN

PRINT　 a

ELSE

PRINT　 b

END IF

END

算法二：

第一步：输入a,b的数值；

第二步：判断a,b的大小关系，若b > a，则将b的值赋予a；否则直接执行第三步；

第三步：输出a的值，结束。

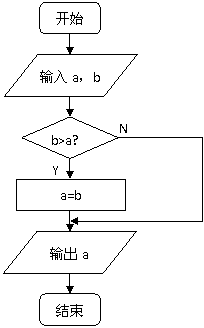(程序框图如右图)

程序如下：(“IF-THEN”语句)

INPUT“a，b”；a，b

IF　 b＞a　 THEN

a=b

END IF

PRINT　 a

END

点评：1．一个“好”的算法往往像上面教材例题中的“小技巧”，要熟练、有效的使用它们，则需要在大量的算法设计中积累经验。我们也可以先根据自己的思路设计算法，再与 “成形”的、高效的、优秀的算法比较，改进思路，改进算法，以避免重复计算等问题，提高算法设计的水平！

2．我们在平常的训练中尽可能的少引用变量，过多的变量不仅会使得算法和程序变得复杂，而且不利于计算机的执行。为此，我们在练习中要积极思考尽可能少引入变量以及如何才能少引入变量

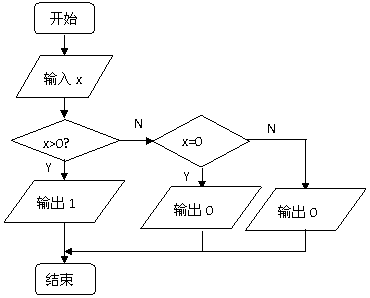例6．高等数学中经常用到符号函数，符号函数的定义为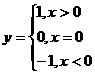，试编写程序输入x的值，输出y的值。

程序一：(嵌套结构)

程序框图：(右图)

程序语言：

INPUT　 x

IF x>0 THEN

y=1

ELSE

IF x=0　 THEN

y=0

ELSE

y=－1

END IF

END IF

PRINT y

END

程序二：(叠加结构)

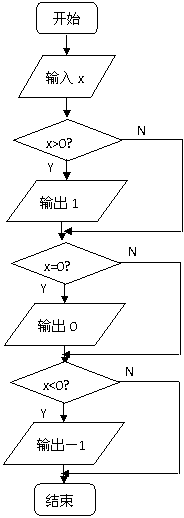程序框图：

程序如下：

INPUT　 x

IF x>0 THEN

y=1

END IF

IF x=0　 THEN

y=0

END IF

IF x<0　 THEN

y=－1

END IF

PRINT y

END

点评：1．条件结构的差异，造成程序执行的不同。当代入x的数值时，“程序一”先判断外层的条件，依次执行不同的分支，才有可能判断内层的条件；而“程序二”中执行了对“条件1”的判断，同时也对“条件2”进行判断，是按程序中条件语句的先后依次判断所有的条件，满足哪个条件就执行哪个语句

5．循环语句

(1)当型循环语句

当型(WHILE型)语句的一般格式为：

WHILE　 条件

循环体

WEND

说明：计算机执行此程序时，遇到WHILE语句，先判断条件是否成立，如果成立，则执行WHILE和WEND之间的循环体，然后返回到WHILE语句再判断上述条件是否成立，如果成立，再执行循环体，这个过程反复执行，直到一次返回到WHILE语句判断上述条件不成立为止，这时不再执行循环体，而是跳到WEND语句后，执行WEND后面的语句。因此当型循环又称“前测试型”循环，也就是我们经常讲的“先测试后执行”、“先判断后循环”。

(2)直到型循环语句

直到型(UNTIL型)语句的一般格式为：

DO

循环体

LOOP　 UNTIL　 条件

说明：计算机执行UNTIL语句时，先执行DO和LOOP　 UNTIL之间的循环体，然后判断 “LOOP　 UNTIL”后面的条件是否成立，如果条件成立，返回DO语句处重新执行循环体。这个过程反复执行，直到一次判断 “LOOP　 UNTIL”后面的条件不成立为止，这时不再返回执行循环体，而是跳出循环体执行“LOOP　 UNTIL　 条件”下面的语句。

因此直到型循环又称“后测试型”循环，也就是我们经常讲的“先执行后测试”、“先循环后判断”。

4．条件语句

(1)“IF-THEN-ELSE”语句

格式：

IF　 条件　 THEN

语句1

ELSE

语句2

END　 IF

说明：在“IF-THEN-ELSE”语句中，“条件”表示判断的条件，“语句1”表示满足条件时执行的操作内容；“语句2”表示不满足条件时执行的操作内容；END　 IF表示条件语句的结束。计算机在执行“IF-THEN-ELSE”语句时，首先对IF后的条件进行判断，如果符合条件，则执行THEN后面的“语句1”；若不符合条件，则执行ELSE后面的“语句2”。

(2)“IF-THEN”语句

格式：

IF　 条件 THEN

语句

END　 IF

说明：“条件”表示判断的条件；“语句”表示满足条件时执行的操作内容，条件不满足时，直接结束判断过程；END　 IF表示条件语句的结束。计算机在执行“IF-THEN”语句时，首先对IF后的条件进行判断，如果符合条件就执行THEN后边的语句，若不符合条件则直接结束该条件语句，转而执行其它后面的语句

3．赋值语句

赋值语句的一般格式：变量=表达式

赋值语句中的“＝”称作赋值号

作用：赋值语句的作用是将表达式所代表的值赋给变量；

要求：

(1)赋值语句左边只能是变量名字，而不是表达式，右边表达式可以是一个常量、变量或含变量的运算式。如：2=x是错误的；

(2)赋值号的左右两边不能对换。赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量。如“A=B”“B=A”的含义运行结果是不同的，如x=5是对的，5=x是错的，A+B=C是错的，C=A+B是对的。

(3)不能利用赋值语句进行代数式的演算。(如化简、因式分解、解方程等)，如

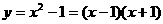
这是实现不了的。在赋值号右边表达式中每一个变量的值必须事先赋给确定的值。在一个赋值语句中只能给一个变量赋值。不能出现两个或以上的“=”。但对于同一个变量可以多次赋值。

2．输出语句

输出语句的一般格式：PRINT“提示内容”；表达式

例如：PRINT“S=”；S

功能：实现算法输出信息(表达式)

要求：

(1)表达式是指算法和程序要求输出的信息；

(2)提示内容提示用户要输出的是什么信息，提示内容必须加双引号，提示内容要用分号和表达式分开。

(3)如同输入语句一样，输出语句可以一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔；输出语句还可以是“提示内容1”；表达式1，“提示内容2”；表达式2，“提示内容3”；表达式3，……”的形式；例如：PRINT “a,b,c:”；a,b,c。

1．输入语句

输入语句的格式：INPUT “提示内容”； 变量

例如：INPUT “x=”； x功能：实现算法的输入变量信息(数值或字符)的功能。

要求：

(1)输入语句要求输入的值是具体的常量；

(2)提示内容提示用户输入的是什么信息，必须加双引号，提示内容 “原原本本”的在计算机屏幕上显示，提示内容与变量之间要用分号隔开；

(3)一个输入语句可以给多个变量赋值，中间用“，”分隔；输入语句还可以是““提示内容1”；变量1，“提示内容2”；变量2，“提示内容3”；变量3，……”的形式。例如：INPUT“a=，b=，c=，”；a，b，c。

算法是高中数学课程中的新内容，本章的重点是算法的概念和算法的三种逻辑结构

预测2010年高考对本章的考察是：以选择题或填空题的形式出现，分值在5分左右，本讲考察的热点是识别程序和编写程序

1．经历将具体问题的程序框图转化为程序语句的过程，理解几种基本算法语句--输入语句、输出语句、赋值语句、条件语句、循环语句，进一步体会算法的基本思想；

4．关于几何概型：

(1)我们是就平面的情形给出几何概型的，同样的方法显然也适用于直线或空间的情形，只需将“面积”相应地改变为“长度”、“体积”；

(2)几何概型并不限于向平面(或直线、空间)投点的试验，如果一个随机试验有无限多个等可能的基本结果，每个基本结果可以用平面(或直线、空间)中的一点来表示，而所有基本结果对应于一个区域Ω，这时，与试验有关的问题即可利用几何概型来解决