
题目列表(包括答案和解析)
1.给出下列四个函数:① ,②
,② ,③
,③ ,④
,④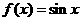 ,其中在
,其中在 是增函数的有( )
是增函数的有( )
A.0个 B.1个 C.2 个 D.3个
例1.判断函数 的奇偶性及周期性。
的奇偶性及周期性。
分析:<1>定义域:
 ∴ f(x)定义域关于原点对称,如图:
∴ f(x)定义域关于原点对称,如图:
又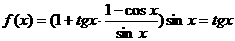
∴ f(-x)=-f(x),
∴ f(x)周期p的奇函数。
评述:研究性质时关注定义域。
例2.<1>设f(x)定义在R上的偶函数,且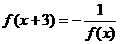 ,又当x∈[-3,-2]时,f(x)=2x,求f(113.5)的值。
,又当x∈[-3,-2]时,f(x)=2x,求f(113.5)的值。
<2>已知f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=x+1.求f(x)在(1,2)上的解析式。
解:<1>∵ 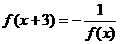
∴  , ∴ f(x)周期T=6,
, ∴ f(x)周期T=6,
∴ f(113.5)=f(6´19-0.5)=f(-0.5).
当x∈(-1,0)时,x+3∈(2,3).
∵ x∈(2,3)时,f(x)=f(-x)=2x.
∴ f(x+3)=-2(x+3).
∴ 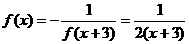 ,
,
∴  .
.
<2>(法1)(从解析式入手)
∵ x∈(1,2), 则-x∈(-2,-1),
∴ 2-x∈(0,1), ∵ T=2.
∵ f(x)=f(-x)=f(2-x)=2-x+1=3-x.
∴ f(x)=3-x, x∈(1,2).
 小结:由奇偶性结合周期性,将要求区间上问题转化为已知解析式的区间上。
小结:由奇偶性结合周期性,将要求区间上问题转化为已知解析式的区间上。
(法2)(图象)
f(x)=f(x+2)
如图:x∈(0,1), f(x)=x+1.
x∈(-1,0)→f(x)=-x+1.
x∈(1,2)→f(x)=-(x-2)+1=3-x.
注:从图象入手也可解决,且较直观。
例3.<1>若x∈(1,2)时,不等式(x-1)2<logax恒成立,求a的取值范围。
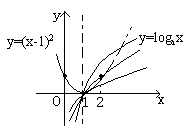 <2>已知二次函数f(x)=x2+ax+5对任意t都有f(t)=f(-4-t),且在闭区间Z[m,0]上有最大值5,最小值1,求m的取值范围。
<2>已知二次函数f(x)=x2+ax+5对任意t都有f(t)=f(-4-t),且在闭区间Z[m,0]上有最大值5,最小值1,求m的取值范围。
分析:<1>设 y1=(x-1)2, y2=logax
x∈(1,2),即x∈(1,2)时,曲线y1在y2的下方,如图:
∴ a=2时,x∈(1,2)也成立,∴a∈(1,2].
小结:①数形结合 ②变化的观点
③注意边界点,a=2,x取不到2, ∴仍成立。
<2>∵f(t)=f(-4-t), ∴ f(-2+t)=f(-2-t)
∴ f(x)图象关于x=-2对称, ∴ a=4, ∴ f(x)=x2+4x+5.
∴ f(x)=(x+2)2+1, 动区间:[m,0],
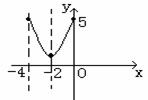 ∵ x∈[m,0], [f(x)]max=5, [f(x)]min=1,
∵ x∈[m,0], [f(x)]max=5, [f(x)]min=1,
∴ m∈[-4,0].
小结:函数问题,充分利用数形结合的思想,并应用运动变化的观点研究问题。如二次函数问题中常见问题,定函数动区间及动函数和定区间,但两类问题若涉及函数最值,必然要考虑函数的单调区间,而二次函数的单调性研究关键在于其图象对称轴的位置。以发展的眼光看,还可解决一类动直线定曲线相关问题。
例4.已知函数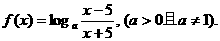
(I)判定f(x)在x∈(-∞,-5)上的单调性,并证明。
(II)设g(x)=1+loga(x-3),若方程f(x)=g(x)有实根,求a的取值范围。
分析:(I)任取x1<x2<-5,
则: ,
,
∵ (x1-5)(x2+5)-(x1+5)(x2-5)=10(x1-x2)<0
又 (x1-5)(x2+5)>0 且(x1+5)(x2-5)>0
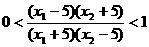 ,
,
∴ 当a>1时,f(x1)-f(x2)<0, ∴ f(x)单调递增,
当0<a<1时,f(x1)-f(x2)>0,∴f(x)单调递减。
(II)若f(x)=g(x)有实根,即: 。
。
∴ 
∴ 即方程: 有大于5的实根。
有大于5的实根。
(法1)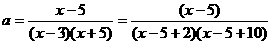 (∵ x>5)
(∵ x>5)
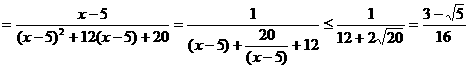
∴  .
.
(法2)(实根分布) (1)有大于5的实根,
(1)有大于5的实根,
方程(1)化为:ax2+(2a-1)x-15a+5=0.
∵ a>0, ∴Δ=64a2-24a+1≥0.
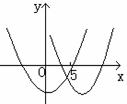 ①有一根大于5
①有一根大于5  .
.
②两根均大于 .
.
小结:实根分布即利用二次函数图象及不等式组解决问题。用此数形结合方法解决问题时,具体步骤为:①二次函数图象开口方向。②图象对称轴的位置。③图象与x轴交点。④端点函数值的符号。此题(2)中,也可以用韦达定理解决。
小结:
函数部分是高考考察重点内容,应当对其予以充分的重视,并配备必要例题,理顺基本方法体系。
练习:
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],m+n≠0时,有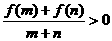 。
。
<1>用定义证明f(x)在[-1,1]上是增函数。
<2>若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围。
7.函数的图象
<1>基本函数图象
<2>图象变换 ①平移 ②对称(取绝对值) ③放缩
易错点:复合变换时,有两种变换顺序不能交换。如下:
<I>取绝对值(对称)与平移
例:由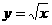 图象,经过如何变换可得下列函数图象?
图象,经过如何变换可得下列函数图象?
<1>  <2>
<2>
分析:<1> 
<2> 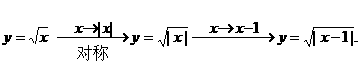
评述:要由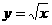 得到
得到 只能按上述顺序变换,两顺序不能交换。
只能按上述顺序变换,两顺序不能交换。
<II>平移与关于y=x对称变换
例:y=f(x+3)的反函数与y=f-1(x+3)是否相同?
分析:①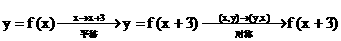 的反函数。
的反函数。
②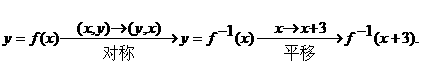
∴两个函数不是同一个函数(也可以用具体函数去验证。)
6.比大小问题
基本方法:<1>粗分。如以“0”,“1”,“-1”等为分界点。
<2>搭桥 <3>结合单调性,数形结合
<4>比差、比商 <5>利用函数图象的凸凹性。
5.函数的奇偶性,单调性,周期性。
关注问题:<1>判定时,先考察定义域。
<2>用定义证明单调性时,最好是证哪个区间上的单调性,在哪个区间上任取x1及x2。
<3>求复合函数单调区间问题,内、外层函数单调区间及定义域,有时需分类讨论。
<4>由周期性及奇偶性(对称性)求函数解析式。
<5>“奇偶性”+“关于直线x=k”对称,求出函数周期。
4.值域问题
基本方法:<1>化为基本函数--换元(新元范围)。化为二次函数,三角函数,……并结合函数单调性,结合函数图象,求值域。
<2>均值不等式:--形如和,积,及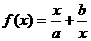 形式。注意识别及应用条件。
形式。注意识别及应用条件。
<3>几何背景:--解析几何如斜率,曲线间位置关系等等。
易错点:<1>考察定义域
<2>均值不等式使用条件
3.关于对应法则
注:<1>分段函数,不同区间上对应法则不同
<2>联系函数性质求解析式
2.关于定义域
<1>复合函数的定义域,限制条件要找全。
<2>应用问题实际意义。
<3>求值域,研究函数性质(周期性,单调性,奇偶性)时要首先考察定义域。
<4>方程,不等式问题先确定定义域。
1.集合与映射
<1>认清集合中的代表元素
<2>有关集合运算中,辨清:子集,真子集,非空真子集的区别。还应注意空集的情形,验算端点。
10.分段函数 11. 函数方程及不等式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com