
题目列表(包括答案和解析)
22、解:(1)由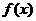 为偶函数知
为偶函数知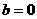 ,又
,又 ,得
,得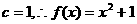
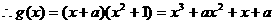 ,从而
,从而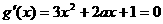 有实数解
有实数解
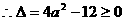 ,解得
,解得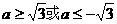
(2)由题意 ,得
,得

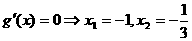
又当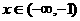 是,
是, ,
, 时,
时, ,
, 时,
时,
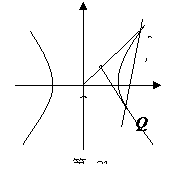
 在
在 取极大值,在
取极大值,在 取极小值
取极小值
又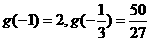 ,方程
,方程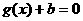 即
即 有三个不同的实数解
有三个不同的实数解
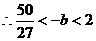 ,解之得
,解之得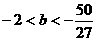
21、解:设出售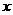 吨时,利润是
吨时,利润是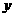 元,
元,
则 =
= 依题意可知,当
依题意可知,当 时,
时,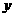 有最大值,则
有最大值,则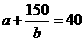 ①当
①当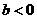 或
或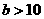 时,
时, <0 ,故
<0 ,故 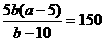 ②
②
解①②得 .
.
20、解:(Ⅰ)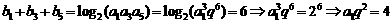 .∵
.∵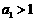 ,
,
∴ .又
.又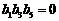 ,
,
若 ,则
,则 ,即
,即 ,这与
,这与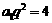 矛盾,
矛盾,
故 .∴
.∴ ,
,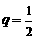 ,
, .∴
.∴ .
.
(Ⅱ)∵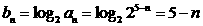 ,∴
,∴ 是首项为
是首项为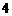 ,公差为
,公差为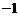 的等差数列,∴
的等差数列,∴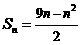 ,
,
 .故
.故 是首项为
是首项为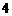 ,公差为
,公差为 的等差数列.
的等差数列.
∵ 时,
时,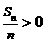 ;
;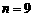 时,
时,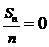 ;
; 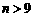 时,
时, .
.
故当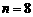 或
或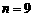 时,
时,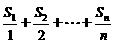 最大.
最大.
19、解:(1)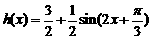 ,单调递减区间是
,单调递减区间是
(2).∵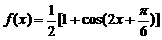 ,又
,又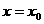 是函数
是函数 图像的一条对称轴,
图像的一条对称轴,
∴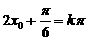 即
即 ∴
∴ ∴当k为偶数时,
∴当k为偶数时,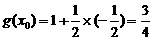 ;
;
当k为奇数时,
18、解:(Ⅰ)设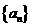 的公差为
的公差为 ,
, 的公比为
的公比为 ,则依题意有
,则依题意有 且
且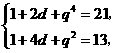
解得 ,
, .所以
.所以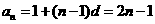
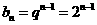 .
.
(Ⅱ)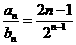 .
.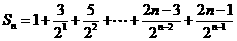 , ①
, ①
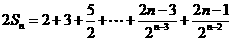 ,
②
,
②
②-①得: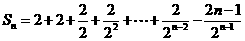 ,
,


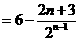 .
.
17、解: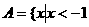 或
或
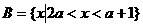
要使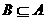 ,则
,则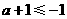 或
或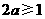 则
则 或
或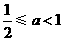
13、-2
-
 2 14、1 15、18 16 4
2 14、1 15、18 16 4
22.(本小题满分12分)已知 为偶函数,曲线
为偶函数,曲线 过点
过点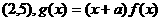
(1)若曲线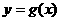 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围
的取值范围
(2)若当 时函数
时函数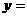
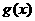 取得极值,且方程
取得极值,且方程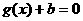 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围
的取值范围
答案:1--6 DCDABA 7--12 AAAAAA
21. (本小题12分)生产某种产品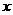 吨时,所需费用是
吨时,所需费用是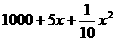 元,当出售这种产品
元,当出售这种产品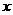 吨时,每吨价格是
吨时,每吨价格是 (
( 是常数)元,如果生产出来的这种产品能全部出售,那么当产量是150吨时,利润最大,并且这时每吨的价格是40元,求
是常数)元,如果生产出来的这种产品能全部出售,那么当产量是150吨时,利润最大,并且这时每吨的价格是40元,求 的值.
的值.
20.(本小题满分12分)已知数列 是首项
是首项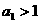 ,公比
,公比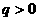 的等比数列.设
的等比数列.设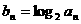
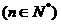 , 且
, 且 ,
,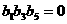 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设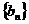 的前
的前 项和为
项和为 ,求当
,求当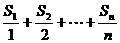 最大时
最大时 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com