
题目列表(包括答案和解析)
6.已知二次函数y=x2-2ax+1在区间(2,3)内是单调函数,则实数a的取值范围是( )
A.a 2或a
2或a 3 B.2
3 B.2 a
a 3 C.a
3 C.a -3或a
-3或a -2 D.-3
-2 D.-3 a
a -2
-2
5.(09厦门一中)已知函数①y=2x;②y=log2x;③y=x-1;④ .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是( )
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是( )
 A.②①③④ B.②③①④ C.④①③② D.④③①②
A.②①③④ B.②③①④ C.④①③② D.④③①②
4.(09厦门质检)设 的大小关系是( )
的大小关系是( )
A. 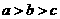 B.
B. 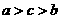 C.
C. 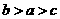 D.
D. 
3.(2009湖南卷)若 a<0,
a<0, >1,则( )
>1,则( )
A.a>1,b>0 B.a>1,b<0 C. 0<a<1, b>0 D. 0<a<1, b<0
2.(2009年广东卷)若函数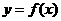 是函数
是函数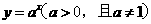 的反函数,且
的反函数,且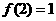 ,则
,则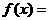 ( )
( )
A. B.
B.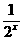 C.
C.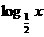 D.2
D.2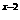
1.(2009湖南卷) 的值为( )
的值为( )
A. B.
B.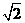 C.
C. D.
D. 
3. (
(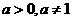 )与
)与 互为反函数.
互为反函数.
当 时,
时, 的
的 值越大,越靠近
值越大,越靠近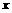 轴;当
轴;当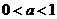 时,则相反.
时,则相反.
《规范解答》
[真题2] (2009天津卷)设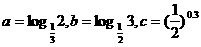 ,则( )
,则( )
A. a<b<c B. a<c<b C .b<c<a D. b<a<c
[命题探究] 本题主要考查对数函数和指数函数的性质。考题的命制,利用对数函数、指数函数的性质比较数的大小,达到了考查考生灵活应用对数函数、指数函数性质的目的,较好地体现了重视基础的命题特点。
[技巧点拨] 比较两个幂值和两个对数值大小的方法
(1)若是两个幂值的大小的比较,则首先分清底数相同还是指数相同,如果底数相同,可以利用指数函数的单调性;如果指数相同,可以转化为底数相同,也可以借助图像;如果底数不同,指数也不同,就要利用中间量进行比较。
(2)若是两个对数值的大小比较,如果底数相同,可以利用对数函数的单调性;如果底数不相同,可以利用换底公式化为同底数的对数;如果底数、真数都不相同,就要注意与0比较或与1比较。
《规范解答》
[真题3] (2009全国卷)函数 的图像( )
的图像( )
(A)关于原点对称 (B)关于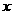 轴对称 (C)关于
轴对称 (C)关于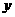 轴对称 (D)关于直线
轴对称 (D)关于直线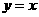 对称
对称
[命题探究] 本题考查对数函数及对称知识,考查了考生推断命题真假的能力。
[课本探源] 本题是人教版数学必修1第75页B组第4题“已知 ,
,
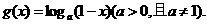 (1)求
(1)求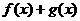 的定义域;(2)判断
的定义域;(2)判断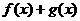 的奇偶性,并说明理由。”的改编题。这里,函数的化简等,只需要扎实的基本功,一些简单的对数运算法则。
的奇偶性,并说明理由。”的改编题。这里,函数的化简等,只需要扎实的基本功,一些简单的对数运算法则。
[知识链接]
对数运算:
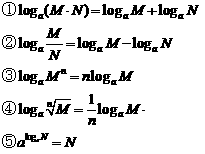

《规范解答》
[真题4] (2009江苏卷改编)设 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求 的取值范围; (2)求函数
的取值范围; (2)求函数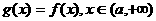 的最小值.
的最小值.
[命题探究] 本题主要考查函数的概念、性质、图象及解绝对值不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。对第(1)问,可以利用条件将问题化为绝对值不等式求解;对第(2)问,可转化为动曲线(动二次函数图像)、动区间的二次函数的最值问题去解决,具体方法见上份资料。本题的设计不重技巧而重通性通法,并且紧扣书本,对《考试大纲》的重点问题重点考查要求。我们应从基础知识到基本方法,再由基本训练到形成能力,这样样才能扎扎实实、一步一个脚印地搞好这一部分的复习。
《规范解答》
高考真题解密
基本初等函数跟踪训练
2.对数函数:如果 (
( )的
)的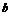 次幂等于
次幂等于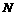 ,
,
就是 ,数
,数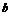 就叫做以
就叫做以 为底的
为底的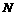 的对数,
的对数,
记作 (
( ,负数和零没有对数);
,负数和零没有对数);
其中 叫底数,
叫底数, 叫真数.
叫真数.
1.
指数函数: (
(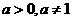 ),定义域R,
),定义域R,
值域为(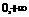 ).
).
⑴①当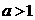 ,指数函数:
,指数函数: 在定义域上为增函数;
在定义域上为增函数;
②当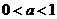 ,指数函数:
,指数函数: 在定义域上为减函数.
在定义域上为减函数.
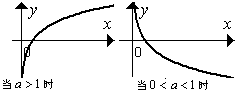 ⑵当
⑵当 时,
时, 的
的 值越大,越靠近
值越大,越靠近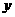 轴;
轴;
当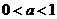 时,则相反.
时,则相反.
冲刺阶段精神因素不可忽视,良好的心态是成功的保证,高考要向良好心态要分,为什么有些学生平时月考,他们往往会考得很好,而高考中会考砸呢?实际上心理素质的提高对有些学生来说比知识水平的提高更重要。常常碰到考生在考场上心慌意乱,走出考场又变得头脑清晰,在冲刺阶段进行心理调适很重要,心态好才能复习高效,才可能在高考中取得高分。高考不仅是知识的比赛和智力的竞争,也是思维品质的考察和心理素质的较量。只要大家精心准备、充满自信、沉着应战,就一定能取的理想高考成绩!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com