
题目列表(包括答案和解析)
3.(第4届加拿大中学生竞赛试题)证明方程x3+113=y3没有x 和y的正整数解.
2.(1989年吉林初中预选赛试题)已知n(n≥2)个相异自然数的和与积相等,求此n的值及n个自然数.
1. 选择题
(1)如果a、b为不超过10的自然数,那么能使方程ax=b的解大于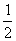 而小于
而小于 的a、b有( ).
的a、b有( ).
(A) 五组 (B)四组 (C)三组 (D)两组
(2)(1984年重庆初中竞赛题)如果α、β、γ是三角形三内角,x=α+β,y=β+γ,z=γ+α,那么x,y,z中锐角个数的错误判断应是( ).
(A) 可能没有锐角 (B)可能有一个锐角
(C)可能有两个锐角 (D)最多有一个锐角
(3)(1978年重庆竞赛题)a、b、c是三角形三边,由a-b<c可导出( ).
(A)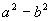 <c2(B)a2-b2>c2(C)a2-b2=c2(D)以上结论都不对
<c2(B)a2-b2>c2(C)a2-b2=c2(D)以上结论都不对
2.分类讨论举例
下面我们用分类讨论的思想方法来解决一些国内外数学竞赛问题.
例2 (第4届加拿大中学生竞赛题)设a和n是相异的实数,证明存在整数m和n使得am+bn<0,bm+an>0.
证明 既然a,b为相异实数,那么必有a-b<0或a-b>0.
当a-b<0时,就取m=1,n=-1,验证和满足所给不等式;
当a-b>0时,就取m=-1,n=1,显然也满足所给不等式.
例3 (1956年上海市竞赛题)从1到100这一百个自然数中,每次取2个,要它们的和大于100,有多少种取法?
解 因为每次所取的两数不等,所以可以按较大(或较小)的数的取值来分类考虑:
较大的数取100时,另一数有99种取法;
较大的数取99时,另一数有97种取法;
……
较大的数取51时,另一数有一种取法;而50以下的任何两数都不能组成符合条件的数对,故共有1+3+5…+97+99=2500种取法.
按照某个确定的自然数为模的剩余类分类是数学竞赛中经常出现的问题之一.
例4 求证:从任意n个整数a1,a2,…,an中,一定可以找到若干个数,使它们的和可被n整除.
证明 考察如下的n个和,a1,a1+a2,a1+a2+a3,…,a1+a2+…+an.
若其中至少有一个能被n的整除,则结论成立;
若其中没有一个能被n整除;则将他们按模n的剩余类至多可分为余数为1,余数为2,…,余数为n-1的n-1个类.因此,这几个整数中至少有两个整数a1+a2+…+ak和a1+a2+a3+ak+…+al(l>k)对模n有相同的余数.
这时和数ak+1+…+al=(a1+a2+…+ak+…+a1)-(a1+a2+…+ak)显然可被n整除,即结论成立.
说明:本例通过分类制造“抽屉”,体现了分类思想有“抽屉原则”的完美结合.
在给定的几何条件下,由于图形的形状或位置不同含有不同的结果或需用不同的方法处理,这就引出了几何中的分类讨论问题.
例5 (1989年武汉、广州等五市初中数学联赛题)△ABC中,∠C=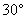 ,BM是中线,AC=2a,若沿BM将三角形对折起来,那个两个小三角形ABM和BCM重叠部分的面积恰好等于△ABC面积的四分之一.试求△ABC的面积.
,BM是中线,AC=2a,若沿BM将三角形对折起来,那个两个小三角形ABM和BCM重叠部分的面积恰好等于△ABC面积的四分之一.试求△ABC的面积.
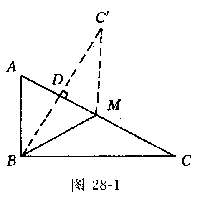
解①若原三角形中,∠ABM>∠CBM,则对折后如图28-1,其中 是对折后C点所落位置,△BMD是重叠部分.依题意得
是对折后C点所落位置,△BMD是重叠部分.依题意得

∴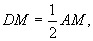 即D为AM的中点.
即D为AM的中点.
又
∴D是BC的中点.
由∠ADB=∠MD 知,△ABD≌△M
知,△ABD≌△M D,∴AB=
D,∴AB= M=CM=
M=CM=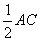 .而∠ACB=
.而∠ACB=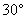 ,∴∠ABC=
,∴∠ABC= .
.
由AC=2a,可得AB=a,BC=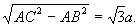
∴
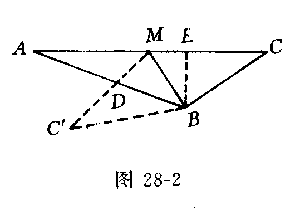
(2)若原三角形中∠ABM<∠CBM,对折后如图28-2.如上证明,可得D为AB,M 的中点.
的中点.
∴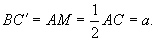 于是BC=B
于是BC=B =a.
=a.
过B作△ABC的高BE.∵∠ACB=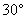 ,
,
∴
∴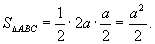
(3)显然,∠ABM=∠CBM不合题意.
列6 设一条曲线的两端在单位正方形的周界上;并且这条曲线将正方形分成面积相等的两部分.证明这条曲线的长度不小于1.
证明 (如图28-3)设曲线PQ分正方形ABCD为面积相等的两部分S1,S2.又M、N、E、F分别为正方形的边的中点.因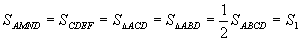 的面积,故曲线PQ与线段MN、EF、AC、BD必各至少有一个公共点.现按P、Q的位置来分类讨论.
的面积,故曲线PQ与线段MN、EF、AC、BD必各至少有一个公共点.现按P、Q的位置来分类讨论.
不失一般性,不妨设P在AB上,这时,

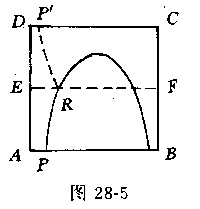
① Q在对边CD上(图28-4).如上所述,曲线PQ与MN至少有一公共点(设为R),则PQ=PR+RQ≥PR+RQ≥MR+RN=MN=1,此时结论正确.
② Q在AB上(图28-5).设曲线PQ与线段EF的一个公共点为R.以EF为对称轴作出PR的对称图形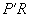 ,则曲线PQ与曲线
,则曲线PQ与曲线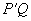 等长.由①知
等长.由①知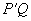 ≥1,故PQ≥1,此时结论也正确.
≥1,故PQ≥1,此时结论也正确.
③ Q在邻边BC或AD之一上(图28-6).令曲线PQ与AC的一个公共点为R,以AC为对称轴作出RQ的对称图形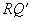 ,则曲线PQ与
,则曲线PQ与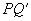 等长.由①知,此时结论亦成立.
等长.由①知,此时结论亦成立.
综上述,对符合条件的任意位置的P、Q均有所述结论.


练习二十八
1. 分类讨论的规则
解题总是在一定的范围(论域)进行的.解题中有时要将题目条件包含的全体对象分成若干类,然后逐类讨论,才能得出正确的解答.因此,分类讨论是数学解题中的一个重要内容.
(1) 分类的规则 分类时首先要明确分类的对象和分类的标准.有时还要对第一次分出的各类进行再分类,这就是第二级分类,类似地有第三级分类、第四级分类、……,这种进行多次分类的现象叫做连续分类.合理的分类不但是正确解题的基础,而且是简捷解题的出发点.
分类的原则是:不重不漏,即每一个题设包含的对象都必须在而且只在所分的一类中.为此,分类时必须做到:
① 一次分类只按一个标准进行;
② 连续分类按层次逐级进行.
(2)枚举和讨论 解决需要讨论的问题的方法是枚举,枚举的基础是正确分类.
例1 求出所有的自然数n,使三个整数n,n+8,n+16都为质数.
解 现将所有自然数n按模为3的剩余类分成三类:
n=3k,3k+1,3k+2.
当n=3k时,只有k=1时,三个整数(3,11,19)都是质数;
当n=3k+1时,n+8=3k+1+8=3(k+3)不是质数;
当n=3k+2时,n+16=3k+2+16=3(k+6)不是质数.
所以满足题设的自然数只有一个3.
17、(本小题满分10分)
⊙ 和⊙
和⊙ 的极坐标方程分别为
的极坐标方程分别为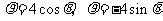 .
.
(Ⅰ)把⊙ 和⊙
和⊙ 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求⊙ ,⊙
,⊙ 交点的直线的垂直平分线的直角坐标方程。
交点的直线的垂直平分线的直角坐标方程。
16、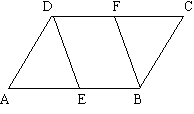 (本小题满分10分)
(本小题满分10分)
已知:如图, ,DE平分
,DE平分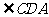 ,BF平分
,BF平分 ,
,
且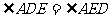 。
。
求证:
15、(本小题满分10分)
求证:(1) ;
(2)
;
(2)  +
+ >2
>2 +
+
14、右面是一个算法的程序框图,当输入的值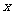 为5时,
为5时,
则其输出的结果是 。
13、由数列的前四项:  ,1 ,
,1 ,  ,
, ,……归纳出通项公式
,……归纳出通项公式
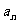 =___ _。
=___ _。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com