
题目列表(包括答案和解析)
2、已知复数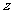 满足
满足 ,则
,则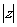 =
=
1、已知集合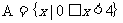 ,
,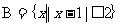 ,则
,则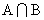 =
,
=
,
1.函数的基本概念 一个函数由它的自变量允许取值的范围(即定义域)和对应关系所确定,并由此确定了函数值的变化范围(即值域).定义域、对应关系、值域称为函数的三要素. (1)求函数的定义域 例1(1982年西安初中竞赛题)已知函数 求自变量取值范围. 解 -2<x<-1,或-1<x<0,或0<x<2,或2<x≤3.或者写成-2<x≤3,且x≠0,2. 例2(1982年大连海运学院研究生招考题)设函数y=f(x)的定义域为[0,1],试求f(x+a)+f(x-a)的定义域(a>0). 解 由 若0<a<时,x∈[a,1-a]; 若a>时,函数关系不存在. (2)关于对应法则 若把自变量比作将要加工的原料,那么对应法则f就是加工手段和规则.正确认识对应法则是深刻理解函数概念的一个重要方面. 例3(美国34届中学生邀请赛题)设f是一个多项式,对所有实数x,f(x2+1)=x4+5x2+3.对所有实数x,求f(x2-1). 分析 若能找到函数的对应法则f,即自变量是怎样“加工处理”的,此题易解,下面给出两种解法. ①配凑法:f(x2+1)=x4+5x2+3 =(x2+1)2+3(x2+1)-1, ∴f(x)=x2+3x-1, ∴f(x2-1)=(x2-1)2+3(x2-1)-1 =x4+x2-3. ②换元法 令 x2+1=t,则x2=t-1. 由f(x2+1)=x4+5x2+3有 f(t)=(t-1)2+5(t-1)+1=t2+3t-1 ∴f(x2-1)=(x2-1)2+3(x2-1)-1 =x4+x2-3. 例4 (1984年上海青少年数学爱好者协会招生试题)设函数f(x)=2x(ax2+bx+c)满足等式f(x+1)-f(x)=2x·x2,求a+b+c的值. 解(待定系数法)f(x)=2x(ax2+bx+c), f(x+1)=2x+1[a(x+1)2+b(x+1)+c] =2·2x[(ax2+bx+c)+2ax+a+b] =2f(x)+2·2x(2ax+a+b) 由f(x+1)-f(x)=2x·x2有 2x(ax2+bx+c)+2·2x[2ax+a+b]=2x·x2, 在上式中, 令x=0得 2a+2b+c=0;① 令x=1得 7a+3b+c=0;② 令x=2得 14a+4b+c=0.③ 由①,②,③解出 a=1,b=-4,c=6, ∴ a+b+c=3. (3)关于函数方程 这个问题是前一个问题的继续,我们把含有未知函数的等式叫函数方程,把寻求未知数的过程,或证明函数方程无解叫解函数方程. 例5 对于一切实数x,y,函数满足f(x·y)=f(x)·f(y),且f(0)≠0.求f(1987)和f(1988). 解 ∵f(x·y)=f(x)·f(y),取y=0,得f(x·0)=f(x)f(0)f(0)=f(x)·f(0).又f(0)≠0,∴f(x)=1,∴f(1987)=f(1988)=1. 例6 (第32届美国中学生数学竞赛题)函数f(x)在x=0处没有定义,但对所有非零实数x有f(x)+2f=3x.满足方程f(x)=f(-x)的实数( ). (A)恰有一个 (B)恰有两个 (C)不存在 (D)有无穷多个,但并非一切非零实数 (E)是一非零实数 解 f(x)+2f=3x.① 以换x得 f+2f(x)= ② 由①,②两式消去f得3f(x)=-3x, ∴f(x)= -x.③ 又由f(x)=f(-x),将③代入得 -x=+x, 即 -2x=0,2-x2=0, ∴x=±.故应选(B). (4)求函数值 例7(1986年北京高一竞赛题) f(x)=(2x5+2x4-53x3-57x+54)1986, 求f[-1]. 解 设,则2t+1=, 即2t2+2t=55. ∴2t5+2t4-53t3-57t+54 =t3(2t2+2t)-53t3-57t+54 =2t3+2t2-2t2-57t+54 =55t-2t2-57t+54 =-2t2-2t+54=-1. ∴f()=(-1)1986=1. 2.正比便函数、反比便函数及一次函数 例8 (1987年浙江省初中竞赛题)已知y=y1+,其中y1与x成正比例,y2与x成反比例,且当x=2和x=3时,y的值都为19.求y与变量x的函数关系式. 解 设y1=k1x,y2=(k1,k2均不为零), 则 y=y1+=k1x+. 将x=2,x=3代入y=y1+得 ∴ y=5x+ 例9(1986年吉林八市初中数学竞赛题)一次函数y=ax+b(a≠0)有一组对应值x=,y=0.试证y=ax+b不能有二组以上的有理数的对应值. 证明 若y=ax+b存在两组不同的有理数对应值(x1,y1),(x2,y2),而函数式为y=a(x-), 故 ∵a≠0,消去a可得(y2-y1)=x1y2-x2y1. ∵x1y2-x2y1是有理数. ∴y2-y1=0,即y1=y2, ∴x1y1-x2y1=0. 即(x1-x2)y1=0. 若y1=0,则x1=,但这与假设矛盾,故不可能. ∴y1≠0,从而x1=x2也不可能. ∴y=ax+b不能有两组以上的有理数的对应值. 3.二次函数 关于二次函数,我们最关心的是应用二次函数的图象和极值定理解一些应用问题. 例10(1987年浙江初中数学竞赛题)设二次函数y=(a+b)x2+2cx-(a-b),其中a,b,c是三角形的三边,且b≥a,b≥c.已知x=-这个二次函数有最小值为-,求△ABC三内角A、B、C的度数. 解散 由题设,二次函数图象的顶点坐标是 (-,-),即(). 于是 ①② 由①得a+b=2c, 代入②得(b-c)+(b-a)=0. ∵b≥a,b≥cb-c=0,b-a=0, 即 a=b=c.△ABC为正三角形,A=B=C=60°. 例11 (1989年全国初中数学竞赛题)如图31-1,△ABC中,D、E分别是边BC、AB上的点,且∠1=∠2=∠3,如果△ABC,△EBD,△ADC的周长依次为m,m1,m2,证明: 证明 由已知可得DE∥AC,进而 △EBD∽△ABC∽△DAC. ① ∴② ③ ∴ 于是有 在这里,我们是将看成关于的二次函数,利用配方法来处理的. 4.其它 下面我们再利用配方法来解一个多元函数的最值问题. 例12 (1978年日本半桥技术科学大学入学题)在边长为a的正三角形中,设点P、Q、R在边BC,CA,AB上运动,并保持的关系,设,△PQR的面积为S. (1)用x、y、z表示S;(2)求S的最大值; (3)求S取最大值时,、、的值. 解(1)S=S△ABC-(S△AQR+S△BRP+S△CPQ). ∵S△ABC=a2, S△AQR=z(a-y)sin60° =z(a-y). 同样S△BRP=x·(a-z), S△CPQ=y(a-x). ∴S=a2-[z(a-y)+x(a-z)+y(a-x)] =a2-a(x+y+z)+ (yz+yx+xy) =a2-a2+(yz+yx+xy) =(yz+yx+xy). ① (2)将z=a-x-y代入①消去z得 S=[(a-x-y)(x+y)+xy] =-[x2+(y-a)y+y2-ay], ∴S=-) ≤ 当x+时,上式取等号, 即x=y=z=时,Smax=a2, (3)根据(2),当S取最大值时,x=y=z=. 在△CPQ内,CQ=,CP=.由余弦定理得 最后,我们把视线转向分段函数的极值问题. 例13(1968-1969年波兰竞赛题)已知两两互异的实数a1,a2,…,an.求由式子(x为实数)y=|x-a1|+|x-a2|+…+|x-an|所定义的函数的最小值. 解 我们首先研究一个简单的事实: 设a<b,则 u=|x-a|+|x-b|= u在a≤x≤b上每一点达到最小值: -a+b. ① 下面我们来研究原命题:对a1,a2,…,an重新按从小到大排序为a1′,a2′,…an′. 于是,当n为偶数,即n=2m时,将原函数重新记为 y=(|x-a1′|+|x-an′|+|x-a2′|+|x-a′n-1| +…+|x-am′|+|x-a′m+1). 令y=|x-a′i|+|x-a′n+1-i|,由①,它在ai≤x≤an+i上取最小值-ai+an+1-i. 又∵每一个区间都包含着下一个区间,即[a1,an] [a2,an-1]…[am,am-1](“”读作包含,如AB,读作A包含B),因此它们的公共区间为[am,am+1].由于在区间[am,am+1]每点上所有yi都取常数最小值,为了方便令x=am或x=am+1于是 y最小值=-a1+an-a2+an-1+…-am+am+1 =-a1-a2-…-am+am+1+am+2+…+an. 当n为奇数时,将原函数记为 y=(|x-a1′|+|x-an′|+|x-a2′|+|x-a′n-1|) +…+(|x-am′|+|x-a′m+2|)+|x-a′m+1|. 类似上面的讨论,当x=am+1时, y最小值=-a1-a2-…-am+am+2+am+3+…+an. 练习三十一 1.选择题 (1)(1989年全国初中数学竞赛题)已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式ab,ac,a+b+c,a-b+c,2a+b,2a-b中,其值为正的式子的个数为( ). (A)2个 (B)3个 (C)4个 (D)4个以上 (2)曲线|y|=x2-1的图象(实线部分)大致形状是( ). (3)(1984年全国竞赛题)若则下列等式正确的是( ). (A)F(-2-x)=-1-F(x) (B) (C)F(x-1)=F(x) (D)F(F(x))=-x 2.填空题 (1)x,y为实数,.则x+xy+x2y的值是_________. (2)(据1990年全国初中竞赛题改)方程7x2-(k+13)x+k2-k-2=0(k是实数)有两个实根α、β,且0<α<1,1<β<2,那么k的取值范围是______. 3.已知f(a+b)=f(a)+f(b),且f(1)=1. 求的值. 4.已知函数y=|x-1|+|x-3|+.试求使y值恒等于常数的x值范围. 5.(1983年全国竞赛题)已知f(x)=ax2-c满足-4≤f(x)≤-1,-1≤f(2)≤5.求f(3)的范围. 6.已知0≤x≤1,0≤y≤1,y-x≥,且x+y+z=1,求函数W=2x+5y+4z的最大、最小值. 7.(1987年浙江初中竞赛题)二次函数f(x)=ax2+bx+c其中a≠0,且a、b、c为实数.对某一常数t,如有af(t)<0,试证:f(x)有不同的两个实数根,其中一个实根比t小,另一实根比t大. 8.(浙江初中竞赛题)函数f(x)对一切实数x满足f(4+x)=f(4-x).若方程f(x)=0恰有三个不同的实根,求这些实根的和是多少? 9.(1985年江苏东台初中数学竞赛题)若z2-2mz+m+6=0的二实数根为a、b,试求(a-1)2+(b-1)2的最小值. 10.(1983年重庆初中数学竞赛题)等边△ABC的边长为a有三个动点P、Q、R分别同时从A、B、C出发沿AB、BC、CA按逆时针方向以各自的速度作匀速直线运动.已知P点由A到B需1秒,Q点从B到C需2秒,R点由C到A需3秒,在一秒钟内,问开始运动多少时间△PQR的面积最小?最小面积是多少?) 11.(1985年苏州初中数学竞赛题)如图,凸四边形ABCD边长依次为2、2、3、1.问在四边形ABCD变形为各种凸四边形的过程中,BD的长的变化范围是什么?B到DC距离的变化范围又是什么? 练习三十一 1.A. D. A. 2. 3. 4.当 5.①②(1)+(2)得③(2)+(3)得-1 6.由z=1-x-y,∴W=4-2x+y.要求W的最大、最小值,只需求y-2x的最大、最小值.设P(x,y)是坐标适合条件的点,则P在以为顶点的内(包括边界).设t=y-2x,则y=2x+t.由t的几何意义W最大值=5W最小值=4. 7.先证 、∈∈8.四个根之和为16. 9.先由 10. ∈11.如图(a)BD最大时,B、A、D在一直线上,BD=3.
10.(第7届加拿大中学竞赛题)对每个实数γ,[γ]表示小于或等于γ的最大整数,例如[6]=6,[π]=3,[-1.5]=-2.在(x,y)平面上指出满足[x]2+[y]2=4的一切点(x,y).

9.证明内接平行四边形的三角形的面积不可能大于这个平行四边形面积的一半.
8.(莫斯科比赛大会预习题)求多项式x2+βx+q的使它在区间[-1,1]上的绝对值为极大值的最小值.
7.(1957年上海竞赛题)设自然数62αβ427为99的倍数,求α、β.
6.(1978年重庆竞赛题)设△ABC中,AB=AC,P为该三角形内一点,且∠APB>∠APC.用间接证法证明:∠BAP<∠CAP.
5.(1984年西安初中竞赛题)求证n5-n可被30整除(n∈整数).
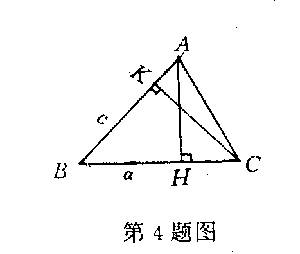
4.(1983年上海初中竞赛题)已知△ABC中∠B为锐角.从顶点A向边BC或它的延长线引垂线,交BC于H,又从顶点C向边AB或它的延长线引垂线交AB于K点.试问当2BH:BC、2BK:BA是整数时,△ABC是怎样三角形?证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com