
题目列表(包括答案和解析)
2. 无锡市二模
20、(1)函数 有一个零点为5,即方程
有一个零点为5,即方程 ,有一个根为5,将
,有一个根为5,将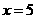 代入方程得
代入方程得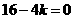 ,∴
,∴ ,∴
,∴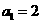 [2分]
[2分]
由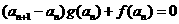 得
得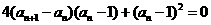
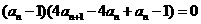
∴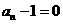 或
或
由(1)知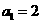 ,∴
,∴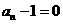 不合舍去
不合舍去
由 得
得 [4分]
[4分]
方法1:由 得
得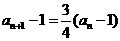
∴数列 是首项为
是首项为 ,公比为
,公比为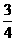 的等比数列
的等比数列
∴ ,∴
,∴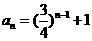
(方法2:由 ---①得当
---①得当 时
时 ----②
----②
①-②得
∴ (
( )即数列
)即数列 是首项为
是首项为 ,公比为
,公比为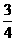 的等比数列
的等比数列
∵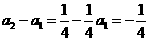 ,∴
,∴ ---------------③
---------------③
由①得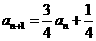 代入③整理得
代入③整理得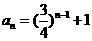 [6分]
[6分]
(2)由(1)知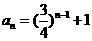
∴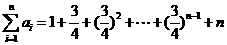 =
= ------8分
------8分
∵对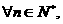 有
有 ,∴
,∴ [8分]
[8分]
∴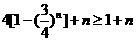 ,即
,即
即所求S 的最小值为1+n.[10分]
的最小值为1+n.[10分]
(3)由 得
得
∴ =
= [12分]
[12分]
令 ,则
,则 ,
, =
=
∵函数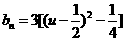 在
在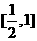 上为增函数,在
上为增函数,在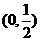 上为减函数[14分]
上为减函数[14分]
当 时
时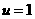 ,
,
当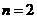 时
时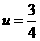 ,
,
当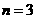 时,
时,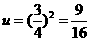 ,
,
当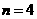 时
时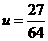 ,
,
∵
 ,且
,且 [16分]
[16分]
∴当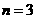 时,
时, 有最小值,即数列
有最小值,即数列 有最小项,最小项为
有最小项,最小项为
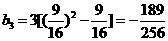
故当 即
即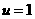 时,
时, 有最大值,即数列
有最大值,即数列 有最大项,最大项为
有最大项,最大项为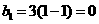 .
.
[18分]
20、(本小题满分18分,第一问6分,第二问4分,第三问8分)
已知函数 ,函数
,函数 其中一个零点为5,数列
其中一个零点为5,数列 满足
满足 ,且
,且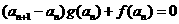 .
.
(1)求数列 通项公式;
通项公式;
(2)求S 的最小值(用含有n的代数式表示);
的最小值(用含有n的代数式表示);
(3)设 ,试探究数列
,试探究数列 是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
19、(I)以O点为原点,指北的方向为y轴建立直角坐标系,则直线OZ的方程为y=3x,
设点A(x0,y0),则x0=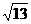 asinβ=3a,y0=
asinβ=3a,y0=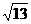 acosβ=2a,即A(3a,2a),
acosβ=2a,即A(3a,2a),
又B(m,0),则直线AB的方程是y= ,
,
由此得到C点坐标为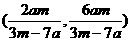 ,
,
 ;[9分]
;[9分]
(II) ,
,
∴当且仅当 时等号成立,[13分]
时等号成立,[13分]
答:征调 海里处的船只时,补给最适宜. [14分]
海里处的船只时,补给最适宜. [14分]
18、(1)当 时,由
时,由 得
得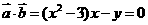 ,
,
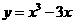 ;(
;( 且
且 )
)
当 时,由
时,由 .得
.得
∴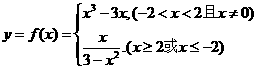 [4分]
[4分]
(2)当 且
且 时,由
时,由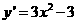 <0,解得
<0,解得 ,[6分]
,[6分]
当 时,
时,
∴函数 的单调减区间为(-1,0)和(0,1)[8分]
的单调减区间为(-1,0)和(0,1)[8分]
(3)对
 ,都有
,都有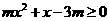 即
即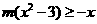 ,也就是
,也就是 对
对
 恒成立,
恒成立,
由(2)知当 时,
时,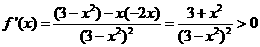
∴函数 在
在 和
和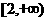 都单调递增[12分]
都单调递增[12分]
又 ,
,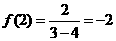
当 时
时 ,∴当
,∴当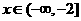 时,
时,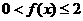
同理可得,当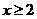 时,有
时,有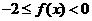 ,
,
综上所述得,对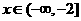
 ,
,
 取得最大值2;
取得最大值2;
∴实数 的取值范围为
的取值范围为 .[15分]
.[15分]
19、(本小题满分14分,第一问9分,第二问5分。)
 如图,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口O
如图,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口O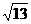 a(a为正常数)海里的北偏东β角的A处共有一个供给科考船物资的小岛,其中已知
a(a为正常数)海里的北偏东β角的A处共有一个供给科考船物资的小岛,其中已知
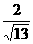 .现指挥部需要紧急征调沿海岸线港口O正东m海里的B处的补给船,速往小岛A装运物资供给科考船.该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S最小时,这种补给最适宜.
.现指挥部需要紧急征调沿海岸线港口O正东m海里的B处的补给船,速往小岛A装运物资供给科考船.该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S最小时,这种补给最适宜.
(1)求S关于m的函数关系式S(m);
(2)应征调m为何值处的船只,补给最适宜?
18、(本小题满分15分,第一问4分,第二问3分,第三问8分。)
已知向量 ,(其中实数
,(其中实数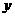 和
和 不同时为零),当
不同时为零),当 时,有
时,有 ,当
,当 时,
时, .
.
(1) 求函数式 ;
;
(2)求函数 的单调递减区间;
的单调递减区间;
(3)若对
 ,都有
,都有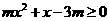 ,求实数
,求实数 的取值范围.
的取值范围.
17、(1)∵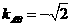 ,
,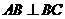 ,∴
,∴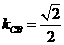 ,∴
,∴ [3分]
[3分]
(2)在上式中,令 ,得
,得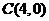 ,∴圆心
,∴圆心
又∵ ,∴外接圆的方程为
,∴外接圆的方程为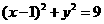 [7分]
[7分]
(3)∵ ,
,
∵圆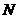 过点
过点 ,∴
,∴ 是该圆的半径
是该圆的半径
又∵动圆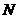 与圆
与圆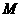 内切,∴
内切,∴ ,即
,即 [11分]
[11分]
∴点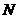 的轨迹是以
的轨迹是以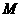 、
、 为焦点,长轴长为3的椭圆,
为焦点,长轴长为3的椭圆,
∴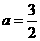 ,
, ,[13分]
,[13分]
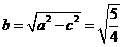 ,
,
∴轨迹方程为 [15分]
[15分]
17、(本小题满分15分,第一问3分,第二问4分,第三问8分。)
 如图,直角三角形
如图,直角三角形 的顶点坐标
的顶点坐标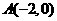 ,直角顶点
,直角顶点 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段 的中点.
的中点.
(1)求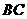 边所在直线方程;
边所在直线方程;
(2)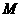 为直角三角形
为直角三角形 外接圆的圆心,求圆
外接圆的圆心,求圆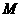 的方程;
的方程;
(3)若动圆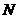 过点
过点 且与圆
且与圆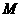 内切,求动圆
内切,求动圆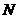 的圆心
的圆心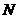 的轨迹方程.
的轨迹方程.
1. 南京市二模
21.(本小题满分14分)
设数列 满足
满足 令
令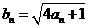
(I)
试证明数列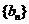 是等差数列,并求数列
是等差数列,并求数列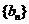 的通项公式;
的通项公式;
(II)
令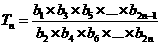 ,是否存在实数
,是否存在实数 ,使得不等式
,使得不等式 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的取值
的取值
范围;若不存在,请说明理由。
(III)比较 与
与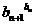 的大小。
的大小。





湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com