
题目列表(包括答案和解析)
21.正数数列{an}的前n项和为Sn,且2.
(1) 试求数列{an}的通项公式;(2)设bn=,{bn}的前n项和为Tn,求证:Tn<.
1. 德兴二模
20.解:(1)由: ,
,
而:
 ,
,
又因为: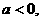 所以:
所以: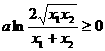 ,即:
,即: 成立。
成立。
(2) 由 恒成立,即只要:
恒成立,即只要: 成立;
成立;
又 ,易知
,易知

令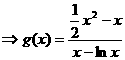 (
( )
)
 ,令:
,令: ,
,

 ,
,
所以: 在
在 上为增函数。
上为增函数。
即:
20.(16分)已知函数 。
。
(1)若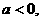 证明:对于任意的两个正数
证明:对于任意的两个正数 ,总有
,总有 成立;
成立;
(2)若对任意的 ,不等式:
,不等式: 恒成立,求
恒成立,求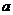 的取值范围。
的取值范围。
19.解 (Ⅰ)设需要新建 个桥墩,
个桥墩,
所以 

(Ⅱ) 由(Ⅰ)知,
令 ,得
,得 ,所以
,所以 =64
=64
当0< <64时
<64时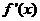 <0,
<0,  在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当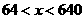 时,
时,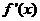 >0.
>0.  在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以 在
在 =64处取得最小值,此时,
=64处取得最小值,此时,
故需新建9个桥墩才能使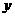 最小。
最小。
19.某地建一座桥,两端的桥墩已建好,这两墩相距 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为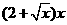 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为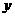 万元。
万元。
(Ⅰ)试写出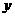 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)当 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使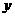 最小?(16分)
最小?(16分)
18.解:(1)椭圆的标准方程: ;
;
(2)设 ),则
),则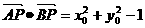 ;
;

则当 时,取到最小值,即:
时,取到最小值,即: ;
;
当 在
在 点时,取到最大值:
点时,取到最大值:
所以: 。
。
(3) 上存在点
上存在点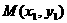 使
使 的充要条件是:
的充要条件是:
易得:当 时存在点M使得:
时存在点M使得:
此时:
 =2。
=2。
18.(15分)已知椭圆以坐标原点为中心,坐标轴为对称轴,且椭圆以抛物线 的焦点为其一个焦点,以双曲线
的焦点为其一个焦点,以双曲线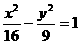 的焦点为顶点。
的焦点为顶点。
(1)求椭圆的标准方程;
(2)已知点 ,且
,且 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。
(3)试问在圆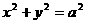 上,是否存在一点
上,是否存在一点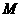 ,使
,使 的面积
的面积 (其中
(其中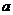 为椭圆的半长轴长,
为椭圆的半长轴长, 为椭圆的半短轴长,
为椭圆的半短轴长, 为椭圆的两个焦点),若存在,求
为椭圆的两个焦点),若存在,求
 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
17.解:(1)略
(2)当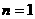 时,
时, ;
;
当 时,
时,
当 为偶数时:
为偶数时: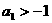
当 为奇数时:
为奇数时:
所以: 。
。
17.(15分)已知数列 的前
的前 项的和为
项的和为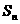 ,数列
,数列 是公比为2的等比数列。
是公比为2的等比数列。
(1)证明:数列 成等比数列的充要条件是
成等比数列的充要条件是 ;
;
(2)设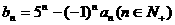 ,若
,若 对
对 恒成立,求
恒成立,求 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com