
题目列表(包括答案和解析)
22、解:(Ⅰ)由题意知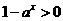
当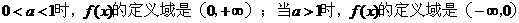
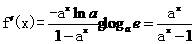
当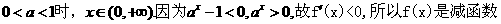
当 ….(4分)
….(4分)
(Ⅱ)因为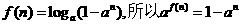
由函数定义域知 >0,因为n是正整数,故0<a<1.
>0,因为n是正整数,故0<a<1.
所以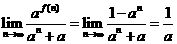 …………6分
…………6分
(Ⅲ)
令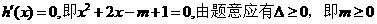
①
当m=0时, 有实根
有实根 ,在
,在 点左右两侧均有
点左右两侧均有 故无极值
故无极值
②
当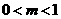 时,
时, 有两个实根
有两个实根
当x变化时, 、
、 的变化情况如下表所示:
的变化情况如下表所示:
|
|
 |
 |
 |
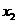 |
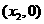 |
 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
 的极大值为
的极大值为 ,
, 的极小值为
的极小值为
③
当 时,
时, 在定义域内有一个实根,
在定义域内有一个实根,
同上可得 的极大值为
的极大值为 ……
……
……10分
综上所述, 时,函数
时,函数 有极值;
有极值;
当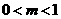 时
时 的极大值为
的极大值为 ,
, 的极小值为
的极小值为
当 时,
时, 的极大值为
的极大值为 …………12分
…………12分
温州三模
22、已知 函数
函数 。
。
(1)求函数 的定义域,并判断
的定义域,并判断 的单调性;
的单调性;
(2)若
(3)当 (为自然对数的底数)时,设
(为自然对数的底数)时,设 ,若函数
,若函数 的极值存在,求实数的取值范围以及函数
的极值存在,求实数的取值范围以及函数 的极值。
的极值。
21、解:(1)设 ,
, ,
, .
.
∵是线段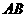 的中点,∴
的中点,∴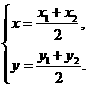 ………2分
………2分
∵ 分别是直线
分别是直线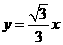 和
和 上的点,∴
上的点,∴ 和
和 .
.
∴ …………4分
…………4分
又 ,∴
,∴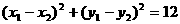 .
…………5分
.
…………5分
∴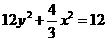 ,∴动点的轨迹
,∴动点的轨迹 的方程为
的方程为 . …………6分
. …………6分
(2)依题意,直线 的斜率存在,故可设直线
的斜率存在,故可设直线 的方程为
的方程为 .
.
设 、
、 、
、 ,
,
则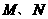 两点坐标满足方程组
两点坐标满足方程组
消去并整理,得 ,
…………8分
,
…………8分
∴ , ①
, ① 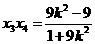 .
②
.
②
∵ ,∴
,∴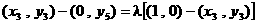
即 ∴
∴ .∵
.∵ 与轴不垂直,∴
与轴不垂直,∴ ,
,
∴ ,同理
,同理 .
………10分
.
………10分
∴
 .
.
将①②代入上式可得 .
…………12分
.
…………12分
21、已知、分别是直线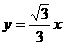 和
和 上的两个动点,线段
上的两个动点,线段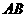 的长为
的长为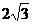 ,是
,是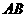 的中点.
的中点.
(1)求动点的轨迹 的方程;
的方程;
(2)过点 任意作直线
任意作直线 (与轴不垂直),设
(与轴不垂直),设 与(1)中轨迹
与(1)中轨迹 交于
交于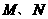 两点,与轴交于点.若
两点,与轴交于点.若 ,
,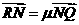 ,证明:
,证明: 为定值.
为定值.
20、解:(1)分别令n=1,2,3,4可求得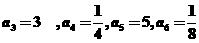 ………2分
………2分
当n为奇数时,不妨设n=2m1, ,则
,则 ,
,  为等差数列,
为等差数列,
 =1+2(m1)=2m1,
即
=1+2(m1)=2m1,
即 。
………4分
。
………4分
当n为偶数时,设n=2m, ,则
,则 ,
,  为等比数列,
为等比数列,
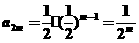 ,故
,故 ,
,
综上所述, ………6分
………6分
(2)
 ………8分
………8分

两式相减:
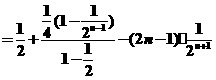 ………10分
………10分
 ,故
,故 ………12分
………12分
注:若求出 猜想出通项(1)问给2分,在上面基础上(2)问解答正确给8分。
猜想出通项(1)问给2分,在上面基础上(2)问解答正确给8分。
20、已知数列 满足
满足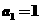 ,
, ,且
,且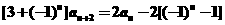 ,
,
(n=1,2,3, ).
).
(1)求 的值及数列
的值及数列 的通项公式;
的通项公式;
(2)令 ,记数列
,记数列 的前n项的和为
的前n项的和为 ,求证:
,求证: <3.
<3.
1. 冀州一模
21. 解析:(Ⅰ)由 得函数
得函数 的定义域为
的定义域为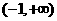 ,
,
 。
……………………………… 2分
。
……………………………… 2分
由 得
得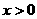 ;由
;由 得
得 ,
,
∴函数 的递增区间是
的递增区间是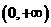 ;递减区间是
;递减区间是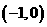 。……………………………… 4分
。……………………………… 4分
(Ⅱ)由(1)知, 在
在 上递减,在
上递减,在 上递增。 ∴
上递增。 ∴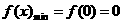
又∵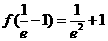 ,
,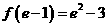 ,且
,且 ,
,
∴ 时,
时, 。
……………………………… 6分
。
……………………………… 6分
∵不等式 恒成立, ∴
恒成立, ∴ ,
,
即
∵ 是整数,∴
是整数,∴ 。
。
∴存在整数 ,使不等式
,使不等式 恒成立。 …………………… 9分
恒成立。 …………………… 9分
(Ⅲ)由 得
得 ,
,
令 ,则
,则 ,
,
由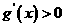 得
得 ;由
;由 得
得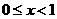 。
。
∴ 在
在 上单调递减,在
上单调递减,在 上单调递增. ……………………………… 11分
上单调递增. ……………………………… 11分
∵方程 在
在 上恰有两个相异的实根,
上恰有两个相异的实根,
∴函数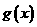 在
在 和
和 上各有一个零点,
上各有一个零点,
∴ ,
,
∴实数 的取值范围是
的取值范围是 ……………………………… 14分
……………………………… 14分
20. 解析:(Ⅰ)由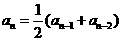 得
得
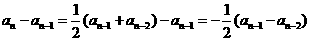 ,
, ……………………2分
……………………2分
又∵  ,∴数列
,∴数列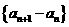 是首项为1公比为
是首项为1公比为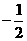 的等比数列,∴
的等比数列,∴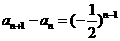 。
。


 ,………4分
,………4分
经检验它对 也成立,∴数列
也成立,∴数列 的通项公式为
的通项公式为 …………5分
…………5分
∵数列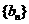 是首相为
是首相为 ,公比为
,公比为 的等比数列。∴
的等比数列。∴ 。………7分
。………7分
(Ⅱ)

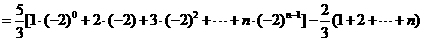
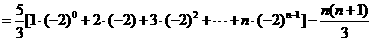 ………………10分
………………10分
记 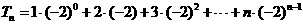 ,
①
,
①
则 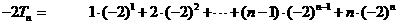 ②
②
由
①-② 得:

∴ ………………………………12分
………………………………12分
∴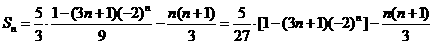 ……………14分
……………14分
19. 解析:(Ⅰ)依题意,圆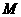 的半径
的半径 等于圆心
等于圆心 到直线
到直线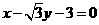 的距离,……2分
的距离,……2分
即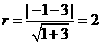 . ∴圆
. ∴圆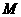 的方程为
的方程为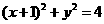 . …………………4分
. …………………4分
(Ⅱ)∵圆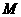 上存在两点关于直线
上存在两点关于直线 对称,
对称,
∴直线 必过圆心
必过圆心 ,
,
∴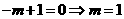 ………………………………………………………7分
………………………………………………………7分
(Ⅲ)设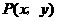 ,由
,由 ,
,
得 ,即
,即  . …………………9分
. …………………9分
∴

 …………………11分
…………………11分
∵点 在圆
在圆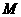 内,∴
内,∴ ,
,
∴ 的取值范围为
的取值范围为 .
……………………………………14分
.
……………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com