
题目列表(包括答案和解析)
3. 深圳一模
19.(本小题满分16分)已知椭圆 的离心率为
的离心率为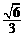 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且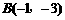 .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
 [解](1)由离心率
[解](1)由离心率 ,得
,得 ,即
,即 . ① ………………2分
. ① ………………2分
又点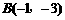 在椭圆
在椭圆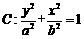 上,即
上,即 . ② ………………4分
. ② ………………4分
解 ①②得 ,
,
故所求椭圆方程为 . …………………6分
. …………………6分
由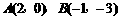 得直线l的方程为
得直线l的方程为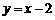 . ………8分
. ………8分
(2)曲线 ,
,
即圆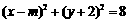 ,其圆心坐标为
,其圆心坐标为 ,半径
,半径 ,表示圆心在直线
,表示圆心在直线
 上,半径为
上,半径为 的动圆.
………………… 10分
的动圆.
………………… 10分
由于要求实数m的最小值,由图可知,只须考虑 的情形.
的情形.
设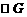 与直线l相切于点T,则由
与直线l相切于点T,则由 ,得
,得 ,………………… 12分
,………………… 12分
当 时,过点
时,过点 与直线l垂直的直线
与直线l垂直的直线 的方程为
的方程为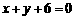 ,
,
解方程组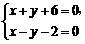 得
得 .
………………… 14分
.
………………… 14分
因为区域D内的点的横坐标的最小值与最大值分别为 ,
,
所以切点 ,由图可知当
,由图可知当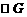 过点B时,m取得最小值,即
过点B时,m取得最小值,即 ,
,
解得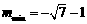 .
………………… 16分
.
………………… 16分
18.(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,
已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个
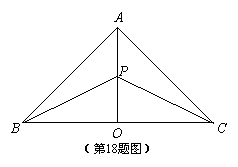 变电站. 记P到三个村庄的距离之和为y. (1)设
变电站. 记P到三个村庄的距离之和为y. (1)设 ,把y表示成
,把y表示成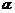 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?
[解](1)在 中,
中,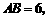 所以
所以 =OA=
=OA=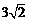 .
.
所以 由题意知
由题意知 . ……………………2分
. ……………………2分
所以点P到A、B、C的距离之和为
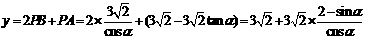 . ……………………6分
. ……………………6分
故所求函数关系式为 .
……………………7分
.
……………………7分
(2)由(1)得 ,令
,令 即
即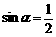 ,又
,又 ,从而
,从而 . ……………………9分.当
. ……………………9分.当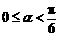 时,
时, ;当
;当 时,
时, 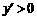 .
.
所以当 时,
时, 取得最小值, ………………… 13分
取得最小值, ………………… 13分
此时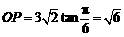 (km),即点P在OA上距O点
(km),即点P在OA上距O点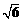 km处.
km处.
[答]变电站建于距O点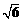 km处时,它到三个小区的距离之和最小. ………… 15分
km处时,它到三个小区的距离之和最小. ………… 15分
17.(本小题满分15分)设等差数列 的前
的前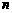 项和为
项和为 且
且 .
.
(1)求数列 的通项公式及前
的通项公式及前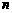 项和公式;
项和公式;
(2)设数列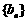 的通项公式为
的通项公式为 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得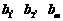
 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
[解](1)设等差数列 的公差为d. 由已知得
的公差为d. 由已知得 ……………………2分
……………………2分
即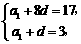 解得
解得 ……………………4分.故
……………………4分.故 . ………6分
. ………6分
(2)由(1)知 .要使
.要使 成等差数列,必须
成等差数列,必须 ,即
,即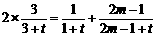 ,……8分.整理得
,……8分.整理得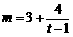 , ……………
11分
, ……………
11分
因为m,t为正整数,所以t只能取2,3,5.当 时,
时, ;当
;当 时,
时, ;当
;当 时,
时, .
.
故存在正整数t,使得 成等差数列. …………………
15分
成等差数列. …………………
15分
2.江苏一模
22. 解:(Ⅰ) ①
①
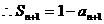 ②
②
②-①得

又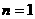 时,
时,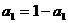

 --------------------------------4分
--------------------------------4分
(Ⅱ)
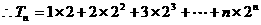 ③
③
 ④
④
③-④得
整理得: -------------------------8分
-------------------------8分
(III)
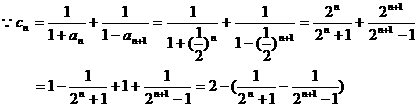
----------------------------------------------------10分
又
-----------------------------------------------------------12分

-----------------------------------------------------------14分
22.已知数列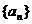 满足:
满足: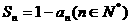 ,其中
,其中 为数列
为数列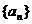 的前
的前 项和.
项和.
(Ⅰ)试求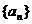 的通项公式;
的通项公式;
(Ⅱ)若数列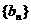 满足:
满足: ,试求
,试求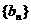 的前
的前 项和公式
项和公式 ;
;
(III)设 ,数列
,数列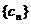 的前
的前 项和为
项和为 ,求证:
,求证: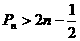 .
.
21.解:(Ⅰ)由题意 的定义域为
的定义域为

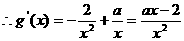
(i)若 ,则
,则 在
在 上恒成立,
上恒成立, 为其单调递减区间;
为其单调递减区间;
(ii)若 ,则由
,则由 得
得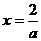 ,
,
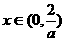 时,
时, ,
, 时,
时,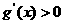 ,
,
所以 为其单调递减区间;
为其单调递减区间; 为其单调递增区间;----------6分
为其单调递增区间;----------6分
(Ⅱ)
所以 的定义域也为
的定义域也为 ,且
,且
令
因为 ,则
,则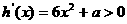 ,所以
,所以 为
为 上的单调递增函数,又
上的单调递增函数,又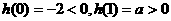 ,所以在区间
,所以在区间 内
内 至少存在一个变号零点
至少存在一个变号零点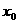 ,且
,且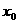 也是
也是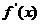 的变号零点,所以
的变号零点,所以 在区间
在区间 内有极值. --------------------12分
内有极值. --------------------12分
21. 已知关于 函数
函数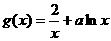 (
( ),
), ,
,
(Ⅰ)试讨论函数 的单调区间;
的单调区间;
(Ⅱ)若 试证
试证 在区间
在区间 内有极值.
内有极值.
20.解:(Ⅰ)由题意知椭圆的焦点在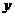 轴上,设椭圆方程为
轴上,设椭圆方程为 ,
,
由题意知 ,
, ,又
,又 则
则 ,
,
所以椭圆方程为 --------------------------------------4分
--------------------------------------4分
(Ⅱ)设 ,由题意,直线
,由题意,直线 的斜率存在,
的斜率存在,
设其方程为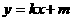 ,与椭圆方程联立
,与椭圆方程联立
即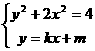 ,
,
则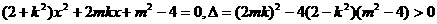
由韦达定理知 ;----------------------------------------6分
;----------------------------------------6分
又 ,即有
,即有
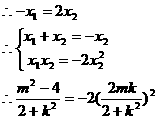 --------------------------------------------8分
--------------------------------------------8分
整理得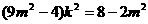
又 时不成立,所以
时不成立,所以 ---------------------------10分
---------------------------10分
得 ,此时
,此时
所以m的取值范围为 .-------------------------------------12分
.-------------------------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com