
题目列表(包括答案和解析)
21.(本小题满分12分)
设椭圆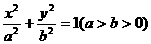 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和 轴正半轴于
轴正半轴于 ,
, 两点,且
两点,且 分向量
分向量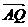 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过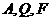 三点的圆恰好与直线
三点的圆恰好与直线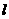 :
: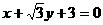 相切,求椭圆方程.
相切,求椭圆方程.
解:(1)设点 其中
其中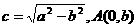 .
.
由 分
分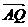 所成的比为8∶5,得
所成的比为8∶5,得 , 2分
, 2分
∴ .①, 4分
.①, 4分
而 ,
,
∴ .
.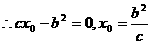 .②, 5分
.②, 5分
由①②知 .
.
∴ . 6分
. 6分
(2)满足条件的圆心为 ,
,
 , 8分
, 8分
圆半径 . 10分
. 10分
由圆与直线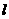 :
: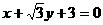 相切得,
相切得, ,
,
又 .
.
∴椭圆方程为 . 12分
. 12分
2.石家庄模拟
20. (本小题满分13分)
已知数列 的前n项和为
的前n项和为 ,且
,且 对任意自然数都成立,其中m为常数,且
对任意自然数都成立,其中m为常数,且 。
。
(I)求证数列 是等比数列;
是等比数列;
(II)设数列 的公比
的公比 ,数列
,数列 满足:
满足:
 ,试问当m为何值时,
,试问当m为何值时,
 成立?
成立?
解:(I)由已知
 (2)
(2)
由 得:
得: ,即
,即 对任意
对任意 都成立
都成立

(II)当 时,
时,
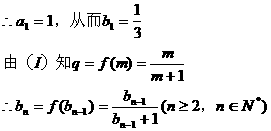



由题意知
 13分
13分
19. (本小题满分14分)
设双曲线 的两个焦点分别为
的两个焦点分别为 ,离心率为2。
,离心率为2。
(I)求此双曲线的渐近线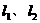 的方程;
的方程;
(II)若A、B分别为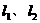 上的点,且
上的点,且 ,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(III)过点 能否作出直线
能否作出直线 ,使
,使 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且 。若存在,求出直线
。若存在,求出直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
解:(I)

 ,渐近线方程为
,渐近线方程为 4分
4分
(II)设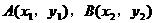 ,AB的中点
,AB的中点

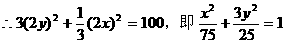
则M的轨迹是中心在原点,焦点在x轴上,长轴长为 ,短轴长为
,短轴长为 的椭圆。(9分)
的椭圆。(9分)
(III)假设存在满足条件的直线
设
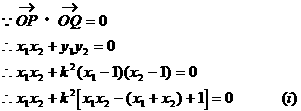

由(i)(ii)得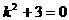
∴k不存在,即不存在满足条件的直线 。 14分
。 14分
1.北京丰台区二模
8、已知函数 ,当点
,当点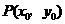 在
在 的图像上移动时,
的图像上移动时,
点 在函数
在函数 的图像上移动.
的图像上移动.
(1) 若点P坐标为( ),点Q也在
),点Q也在 的图像上,求
的图像上,求 的值;
的值;
(2) 求函数 的解析式;
的解析式;
(3) 当 时,试探求一个函数
时,试探求一个函数 使得
使得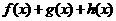 在限定定义域为
在限定定义域为
 时有最小值而没有最大值.
时有最小值而没有最大值.
解:(1)当点 坐标为(
坐标为( ),点
),点 的坐标为
的坐标为 ,…………2分
∵点
,…………2分
∵点 也在
也在 的图像上,∴
的图像上,∴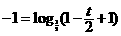 ,即
,即 .……5分
.……5分
(根据函数 的单调性求得
的单调性求得 ,请相应给分)
(2)设
,请相应给分)
(2)设 在
在 的图像上
则
的图像上
则 ,即
,即 ……………………………………8分
而
……………………………………8分
而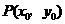 在
在 的图像上,∴
的图像上,∴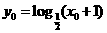 代入得,
代入得,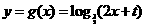 为所求.…………………………………11分
为所求.…………………………………11分
(3) ;或
;或 等. …………………15分
如:当
等. …………………15分
如:当 时,
时,
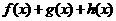

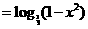
∵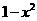 在
在 单调递减, ∴
单调递减, ∴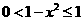 故
故  ,
即
,
即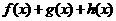 有最小值
有最小值 ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)
(参考思路)在探求 时,要考虑以下因素:①
时,要考虑以下因素:① 在
在 上必须有意义(否则不能参加与
上必须有意义(否则不能参加与 的和运算);②由于
的和运算);②由于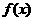 和
和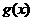 都是以
都是以 为底的对数,所以构造的函数
为底的对数,所以构造的函数 可以是以
可以是以 为底的对数,这样与
为底的对数,这样与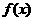 和
和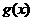 进行的运算转化为真数的乘积运算;③以
进行的运算转化为真数的乘积运算;③以 为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去
为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去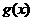 ;⑤乘积的结果可以是
;⑤乘积的结果可以是 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与 轴已有了一个公共点
轴已有了一个公共点 ,故对称轴又应该是
,故对称轴又应该是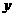 轴或在
轴或在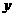 轴的右侧(否则该二次函数的值在
轴的右侧(否则该二次函数的值在 上的值不能恒为正数),即若抛物线与
上的值不能恒为正数),即若抛物线与 轴的另一个公共点是
轴的另一个公共点是 ,则
,则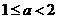 ,且抛物线开口向下.
,且抛物线开口向下.
7、⑴证明:当a>1时,不等式 成立。
成立。
⑵要使上述不等式 成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
⑶请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明。
解:(1)证: ,∵a>1,∴
,∵a>1,∴ >0,
>0,
∴原不等式成立 (6¢)
(2)∵a-1与a5-1同号对任何a>0且a¹1恒成立,∴上述不等式的条件可放宽
为a>0且a¹1 (9¢)
(3)根据(1)(2)的证明,可推知:若a>0且a¹1,m>n>0,则有 (12¢)
(12¢)
证:左式-右式= (14¢)
(14¢)
若a>1,则由m>n>0Þam-n>0,am+n>0Þ不等式成立;
若0<a<1,则由m>n>0Þ0<am-n<1, 0<am+n<1Þ不等式成立.(16¢)
6、已知函数 的最大值为正实数,集合
的最大值为正实数,集合
 ,集合
,集合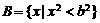 。
。
(1)求 和
和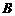 ;
;
(2)定义 与
与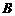 的差集:
的差集: 且
且 。
。
设 ,
, ,
, 均为整数,且
均为整数,且 。
。 为
为 取自
取自 的概率,
的概率, 为
为 取自
取自 的概率,写出
的概率,写出 与
与 的二组值,使
的二组值,使 ,
, 。
。
(3)若函数 中,
中, ,
, 是(2)中
是(2)中 较大的一组,试写出
较大的一组,试写出 在区间[
在区间[ ,n]上的最大值函数
,n]上的最大值函数 的表达式。
的表达式。
解:(1)∵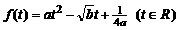 ,配方得
,配方得 ,由
,由 得最大值
得最大值 。……………………………………………………………3分
。……………………………………………………………3分
∴ ,
,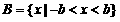 。…………………………6分
。…………………………6分
(2)要使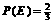 ,
, 。可以使①
。可以使① 中有3个元素,
中有3个元素, 中有2个元素,
中有2个元素,  中有1个元素。则
中有1个元素。则 。…………………………………………………9分
。…………………………………………………9分
② 中有6个元素,
中有6个元素, 中有4个元素,
中有4个元素,  中有2个元素。则
中有2个元素。则 …………………………………………………………………………12分
…………………………………………………………………………12分
(3)由(2)知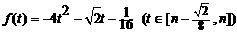 …………………………13分
…………………………13分
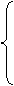

 ………………………………………………18分
………………………………………………18分
5、已知两个向量 ,
,
 .
.
(1)若t=1且 ,求实数x的值;
,求实数x的值;
(2)对tÎR写出函数 具备的性质.
具备的性质.
解:(1)由已知得 ……2分
……2分
 ……4分
……4分
解得 ,或
,或 ……6分
……6分
(2)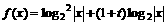 ……8分
……8分
具备的性质:
①偶函数;
②当 即
即 时,
时, 取得最小值
取得最小值 (写出值域为
(写出值域为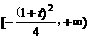 也可);
也可);
③单调性:在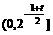 上递减,
上递减, 上递增;由对称性,在
上递增;由对称性,在 上递增,在
上递增,在 递减
……14分
递减
……14分
说明:写出一个性质得3分,写出两个性质得5分,写出三个性质得6分,包括写出函数的零点( ,
, )等皆可。写出函数的定义域不得分,写错扣1分
)等皆可。写出函数的定义域不得分,写错扣1分
14、已知二次函数 同时满足:①不等式
同时满足:①不等式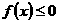 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式 成立。
成立。
设数列 的前
的前 项和
项和 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)试构造一个数列 ,(写出
,(写出 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数 都有
都有 ,且
,且 ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列 的变号数。令
的变号数。令 (
( 为正整数),求数列
为正整数),求数列 的变号数。
的变号数。
解:(1)∵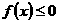 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴ ,
,
当 时,函数
时,函数 在
在 上递增,故不存在
上递增,故不存在 ,使得不等式
,使得不等式 成立。
成立。
当 时,函数
时,函数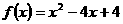 在
在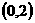 上递减,故存在
上递减,故存在 ,使得不等式
,使得不等式 成立。
成立。
综上,得 ,
,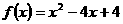 ,∴
,∴ ,
,

∴
(2)要使 ,可构造数列
,可构造数列 ,∵对任意的正整数
,∵对任意的正整数 都有
都有 ,
,
∴当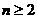 时,
时, 恒成立,即
恒成立,即 恒成立,即
恒成立,即 ,
,
又 ,∴
,∴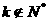 ,∴
,∴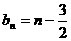 ,等等。
,等等。
(3)解法一:由题设 ,
,
∵ 时,
时, ,
,
∴ 时,数列
时,数列 递增,
递增,
∵ ,由
,由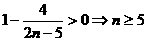 ,
,
可知 ,即
,即 时,有且只有
时,有且只有 个变号数;
个变号数;
又∵ ,即
,即 ,
,
∴此处变号数有 个。
个。
综上得 数列 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
解法二:由题设 ,
,
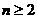 时,令
时,令 ;
;
又∵ ,∴
,∴ 时也有
时也有 。
。
综上得 数列 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com