
题目列表(包括答案和解析)
1. 我国儿童4岁前身高增长的速度最快的是在哪一个年龄段?答:
据有关统计资料, 我国儿童4岁前身高情况有一组统计数据
|
年龄/岁 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
… |
|
身高/米 |
0.52 |
0.63 |
0.73 |
0.85 |
0.93 |
1.01 |
1.06 |
1.12 |
… |
思路分析:: 要判断这一个问题.必须要计算每半年这个群体长高的平均增长率,再加以比较即可,通过计算每半年长高的平均增长率分别是2.2, 2, 2.4, 1.6, 1.6, 1, 1.2可知我国儿童在1.5岁至2岁这一时段身高增长的速度最快
9.某钢材厂要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表:
|
|
A规格 |
B规格 |
C规格 |
|
第一种钢板 |
1 |
2 |
1 |
|
第二种钢板 |
1 |
1 |
3 |
|
需求 |
12 |
15 |
27 |
每张钢板的面积,第一种为1m2,第二种为2 m2,今需要A、B、C三种规格的成品各12、15、27块,请你们为该厂计划一下,应该分别截这两种钢板多少张,可以得到所需的三种规格成品,而且使所用钢板的面积最小?只用第一种钢板行吗?
解:设需要截第一种钢板x张,第二种钢板y张,所用钢板面积为z m2,则
 目标函数z=x+2y
目标函数z=x+2y
作出可行域如图
作一组平行直线x+2y=t,
  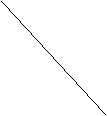    2x+y=15 x+y=12 x+3y=27 x+2y=0 |
由
可得交点 ,
,
但点 不是可行域内的整点,其附近的整点(4,8)或(6,7)可都使z有最小值,
不是可行域内的整点,其附近的整点(4,8)或(6,7)可都使z有最小值,
且zmin=4+2×8=20 或zmin=6+2×7=20
若只截第一种钢板,由上可知x≥27,所用钢板面积最少为z=27(m2);
若只截第二种钢板,则y≥15,最少需要钢板面积z=2×15=30(m2).它们都比zmin大,因此都不行.
|

|
版权所有:()
版权所有:()
8. 已知1 x-y
x-y 2,且2
2,且2 x+y
x+y 4,求4x-2y的范围.
4,求4x-2y的范围.
错解:由于 1 x-y
x-y 2 ①,
2 ①,
2 x+y
x+y 4 ②,
4 ②,
①+② 得3 2x
2x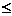 6 ③
6 ③
①×(-1)+② 得:0 2y
2y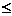 3 ④.
3 ④.
③×2+④×(-1)得. 3 4x-2y
4x-2y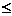 12
12
错因:可行域范围扩大了.
正解:线性约束条件是: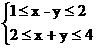
令z=4x-2y,
 画出可行域如右图所示,
画出可行域如右图所示,
由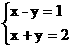 得A点坐标(1.5,0.5)此时z=4×1.5-2×0.5=5.
得A点坐标(1.5,0.5)此时z=4×1.5-2×0.5=5.
由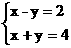 得B点坐标(3,1)此时z=4×3-2×1=10.
得B点坐标(3,1)此时z=4×3-2×1=10.
 5
5 4x-2y
4x-2y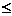 10
10
7. 由 围成的几何图形的面积是多少?
围成的几何图形的面积是多少?
解析:如下图由 围成的几何图形就是其阴影部分,
围成的几何图形就是其阴影部分,
且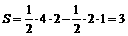 .
.

5.不等式组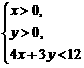 表示的平面区域内的整点(横坐标和纵坐标都是整数的点)共有_____个.
表示的平面区域内的整点(横坐标和纵坐标都是整数的点)共有_____个.
解析:(1,1),(1,2),(2,1),共3个.
6(汕头市金山中学2009届高三上学期11月月考)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
 产品
产品消耗量 资源 |
甲产品 (每吨) |
乙产品 (每吨) |
资源限额 (每天) |
|
煤(t) |
9 |
4 |
360 |
|
电力(kw·h) |
4 |
5 |
200 |
|
劳力(个) |
3 |
10 |
300 |
|
利润(万元) |
6 |
12 |
|
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
解:设此工厂应分别生产甲、乙两种产品x吨y吨,获得利润z万元…………1分
 依题意可得约束条件:
依题意可得约束条件: …………………………5分
…………………………5分
(图2分)
利润目标函数 ………………………………8分
………………………………8分
如图,作出可行域,作直线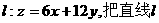 向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时
向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时 取最大值。……10分
取最大值。……10分
解方程组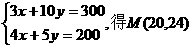 ………………………………12分
………………………………12分
所以生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润。……14分
综合拔高训练
3.(广东省梅州、揭阳两市四校2008届高三第三次联考)已知点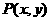 的坐标满足条件
的坐标满足条件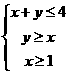 ,点
,点 为坐标原点,那么
为坐标原点,那么 的最大值等于_______,最小值等于____________.
的最大值等于_______,最小值等于____________. 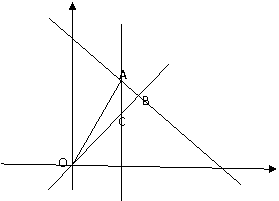
解析: 从图中看出
从图中看出  ,
,
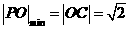 ,
,
4(惠州市2008届高三第三次调研考试)
已知点P(x,y)满足条件 y的最大值为8,则
y的最大值为8,则 .
.
解析:画图,联立方程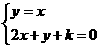 得
得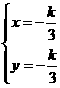 ,代入
,代入
2.已知:点P的坐标(x,y)满足: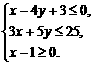 及A(2,0),则|
及A(2,0),则| |·cos∠AOP(O为坐标原点)的最大值是 5
.
|·cos∠AOP(O为坐标原点)的最大值是 5
.
[解析]| |·cos ∠AOP即为
|·cos ∠AOP即为 在
在 上的投影长
上的投影长
由 ∴|
∴| |·cos ∠AOP的最大值为5.
|·cos ∠AOP的最大值为5.
1.已知点 的坐标满足条件
的坐标满足条件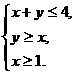 则
则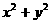 的最大值为.
的最大值为.
 A.
A.  B. 8 C.
16
D. 10
B. 8 C.
16
D. 10
解析:画出不等式组对应的可行域如图所示:易得A(1,1),OA=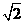 ,
,
B(2,2),OB= ,C(1,3),OC=
,C(1,3),OC= ,故|OP|的最大值为
,故|OP|的最大值为 ,
,
即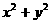 的最大值等于10.故选D.
的最大值等于10.故选D.
6. 定义符合条件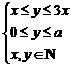 的有序数对
的有序数对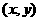 为“和谐格点”,则当
为“和谐格点”,则当 时,和谐格点的个
时,和谐格点的个
数是 .
[解析]作出可行域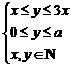 ,数出和谐格点个数为7.
,数出和谐格点个数为7.
考点3 线性规划在实际问题中的应用
题型:在线性规划模型下的最优化问题.
.例1.(2008·揭阳一模) 为迎接2008年奥运会召开,某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”.该厂所用的主要原料为A、B两种贵重金属,已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒,生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒.若奥运会标志每套可获利700元,奥运会吉祥物每套可获利1200元,该厂月初一次性购进原料A、B的量分别为200盒和300盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大利润为多少?
[解题思路] 将文字语言转化为数学式子建立线性规划模型.
将文字语言转化为数学式子建立线性规划模型.
解析:设该厂每月生产奥运会标志和奥运会吉祥物分别为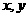 套,月利润为
套,月利润为 元,由题意得
元,由题意得
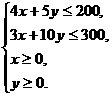 (
(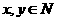 )
)
目标函数为
作出可行域如图所示
目标函数可变形为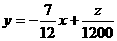 ,
,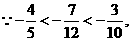
∴当 通过图中的点A时,
通过图中的点A时, 最大,这时Z最大。
最大,这时Z最大。
解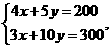 得点A的坐标为(20,24), …………10分
得点A的坐标为(20,24), …………10分
将点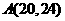 代入
代入 得
得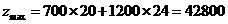 元
元
答:该厂生产奥运会标志和奥运会吉祥物分别为20,24套时月利润最大,最大利润为42800元.
[名师指引]要注意到生产的产品数量是整数这一隐含条件.
★ 抢 分 频 道 ★
基础巩固训练
5. 已知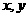 满足约束条件,
满足约束条件,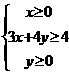 则
则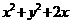 的最小值是( )
的最小值是( )
A.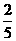 B.
B. C.
C.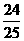 D.
D.
解析: 表示的可行域上的点
表示的可行域上的点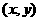 与点
与点 的距离的平方值减1.选D
的距离的平方值减1.选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com