
题目列表(包括答案和解析)
7.某中学高三年级共有12个班级,在即将进行的月考中,拟安排12个班主任老师监考数学,每班1人,要求有且只有8个班级是自己的班主任老师监考,则不同的监考安排方案共有( )
A. 4455种 B.495种 C.4950种 D.7425种
6.已知直线 和平面
和平面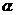 ,则
,则 的一个必要非充分条件是(
)
的一个必要非充分条件是(
)
A. 且
且 B.
B. 且
且
C. 且
且 D.
D. 与
与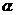 所成角相等
所成角相等
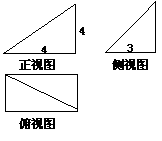
5.已知某几何体的三视图如下,则该几何体的表面积是( )
A. 24 B.
36+
C. 36 D. 36+
4. 设集合
设集合 ,则满足条件
,则满足条件 的集合P的个数是( )
的集合P的个数是( )
A.1 B.3 C.4 D.8
3.若 ,
, ,且
,且 ,则向量
,则向量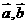 的夹角为( )
的夹角为( )
A. 45° B. 60° C. 120° D.135°
2.已知 ( )
( )
A. B.
B. C.
C. 或
或 D.
D.
1.已知复数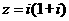 (i为虚数单位),则复数
(i为虚数单位),则复数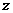 在复平面上所对应的点位于( )
在复平面上所对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19、已知 是二次函数,
是二次函数, 是它的导函数,且对任意的
是它的导函数,且对任意的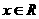 ,
,
恒成立.
(1)求 的解析表达式;
的解析表达式;
(2)设 ,曲线
,曲线 :
: 在点
在点 处的切线为
处的切线为 ,
, 与坐标轴围成的三角形面积为
与坐标轴围成的三角形面积为 .求
.求 的最小值.
的最小值.
解:(1)设 (其中
(其中 ),则
),则 ,
……2分
,
……2分
 .
.
由已知,得 ,
,
∴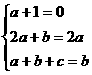 ,解之,得
,解之,得 ,
, ,
, ,
,
∴ . ………………5分
. ………………5分
(2)由(1)得, ,切线
,切线 的斜率
的斜率 ,
,
∴切线 的方程为
的方程为 ,即
,即 .
………………7分
.
………………7分
从而 与
与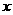 轴的交点为
轴的交点为 ,
, 与
与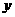 轴的交点为
轴的交点为 ,
,
∴ (其中
(其中 ).
…9分
).
…9分
∴ .
………11分
.
………11分
当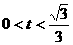 时,
时, ,
, 是减函数;
是减函数;
当 时,
时, ,
, 是增函数.
………………13分
是增函数.
………………13分
∴ .
………………14分
.
………………14分
说明:本题主要考查二次函数的概念、导数的应用等知识,以及运算求解能力.
19、如图,已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
,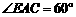 ,
, .
.
(1)在直线 上是否存在一点
上是否存在一点 ,使得
,使得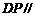 平面
平面 ?请证明你的结论;
?请证明你的结论;
(2)求平面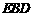 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值.
的余弦值.

 解:(1)线段
解:(1)线段 的中点就是满足条件的点
的中点就是满足条件的点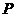 . ……1分
. ……1分
证明如下:
取 的中点
的中点 连结
连结 ,则
,则
 ,
,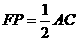 , …………………2分
, …………………2分
取 的中点
的中点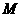 ,连结
,连结 ,
,
∵ 且
且 ,
,
∴△ 是正三角形,∴
是正三角形,∴ .
.
∴四边形 为矩形,
为矩形,
∴ .又∵
.又∵ ,………3分
,………3分
∴ 且
且 ,
,
四边形 是平行四边形.……………………4分
是平行四边形.……………………4分
∴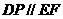 ,
,
而 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 . ……………………6分
. ……………………6分
 (2)(解法1)过
(2)(解法1)过 作
作 的平行线
的平行线 ,过
,过 作
作 的垂线交
的垂线交 于
于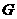 ,连结
,连结 ,
,
∵ ,
,
∴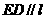 ,
,
 是平面
是平面 与平面
与平面 所成二面角的棱.……8分
所成二面角的棱.……8分
∵平面 平面
平面 ,
,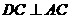 ,
,
∴ 平面
平面 ,
,
又∵ 平面
平面 ,∴
,∴ 平面
平面 ,
,
∴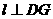 ,
,
∴ 是所求二面角的平面角.………………10分
是所求二面角的平面角.………………10分
设 ,则
,则 ,
, ,
,
∴ ,
,
∴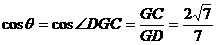 .
…………12分
.
…………12分
(解法2)∵ ,平面
,平面 平面
平面 ,
,
∴以点 为原点,直线
为原点,直线 为
为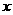 轴,直线
轴,直线 为
为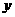 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,则
,则 轴在平面
轴在平面 内(如图).
内(如图).
设 ,由已知,得
,由已知,得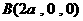 ,
, ,
, .
.
∴ ,
, ,
…………8分
,
…………8分
 设平面
设平面 的法向量为
的法向量为 ,
,
则 且
且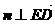 ,
,
∴
∴
解之得
取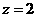 ,得平面
,得平面 的一个法向量为
的一个法向量为
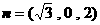 . …………10分
. …………10分
又∵平面 的一个法向量为
的一个法向量为 .
.
 .…………12分
.…………12分
说明:本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.
18、已知函数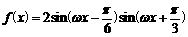 (其中
(其中 为正常数,
为正常数, )的最小正周期为
)的最小正周期为 .
.
(1)求 的值;
的值;
(2)在△ 中,若
中,若 ,且
,且 ,求
,求 .
.
解:(1)∵
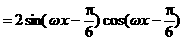
 . ……4分
. ……4分
而 的最小正周期为
的最小正周期为 ,
, 为正常数,
为正常数,
∴ ,
,
解之,得 . ………………………6分
. ………………………6分
(2)由(1)得 .
.
若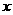 是三角形的内角,则
是三角形的内角,则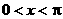 ,
,
∴ .
.
令 ,得
,得 ,
,
∴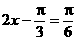 或
或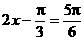 ,
,
解之,得 或
或 .
.
由已知,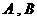 是△
是△ 的内角,
的内角, 且
且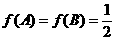 ,
,
∴ ,
, ,∴
,∴ .
………10分
.
………10分
又由正弦定理,得 . ………12分
. ………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com