
题目列表(包括答案和解析)
21.解:(I)双曲线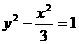 的两焦点为
的两焦点为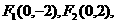
设已知定值为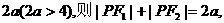
因此,动点P的轨迹E是以
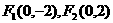 为焦点的长轴长为2a的椭圆; …………2分
为焦点的长轴长为2a的椭圆; …………2分
设椭圆的方程为
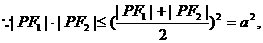
(当且仅当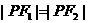 时等号成立) …………4分
时等号成立) …………4分
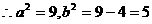
于是,动点P的轨迹E的方程为:
 …………5分
…………5分
(II)设
由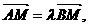
得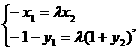
且M、A、B三点共线 …………6分
设三点所在的直线为
①当直线 的斜率存在时,
的斜率存在时,
设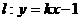
由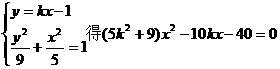 …………7分
…………7分
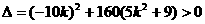 恒成立
恒成立
由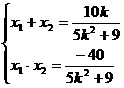
将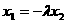 代入并消去
代入并消去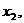
得 …………8分
…………8分
当k=0时,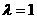
当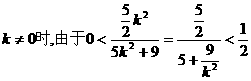
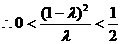
整理得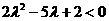
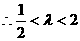 且
且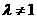 …………10分
…………10分
②当直线 的斜率不存在时,
的斜率不存在时,
A、B分别为椭圆长轴的两个端点;
此时,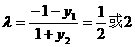 …………11分
…………11分
综上所述,实数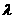 的取值范围为
的取值范围为 …………12分
…………12分
20.解(I)分数在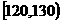 内的频率为:
内的频率为:

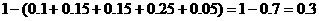 …………2分
…………2分
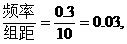
补全后的直方图如右。 …………3分
(II)平均分为:
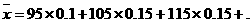
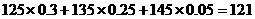 …………6分
…………6分
(III)学生成绩在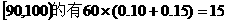 人,
人,
在 的有
的有 人,
人,
在 的有
的有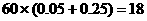 人。
人。
且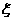 的可能取值0,1,2,3,4 …………8分
的可能取值0,1,2,3,4 …………8分
则

所以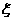 的分布列为:
的分布列为:
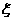 |
0 |
1 |
2 |
3 |
4 |
|
P |
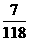 |
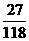 |
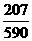 |
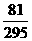 |
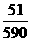 |
…………1分
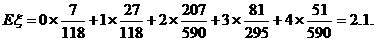 …………12分
…………12分
19.解:设P为AD的中点,
连结EP,PC,
则由已知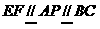
∴EP=PC,FA//EP,EC//BF,AB//PC …………2分
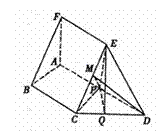 又FA⊥平面ABCD,
又FA⊥平面ABCD,
∴EP⊥平面ABCD
PC、AD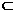 平面ABCD
平面ABCD
故EP⊥PC,EP⊥AD
设FA=a,则EP=PC=PD=a
 …………5分
…………5分
∵M为EC的中点,
∴DM⊥CE
∵BF//EC
∴DM⊥BF。 …………6分
(II)解:取CD的中点Q,连结PQ,EQ
由(I)知PC=PD,CE=DE
∴PQ⊥CD,EQ⊥CD
∴∠EQP为二面角A-CD-E的平面角 …………10分
由(I)可得,在等边 中
中
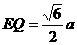
在等腰
在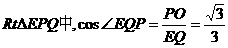
故二面角A-CD-E的余弦值为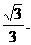 …………12分
…………12分
18.解:(I)由
得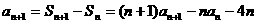
即 …………4分
…………4分
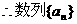 是以1为首项,4为公差的等差数列
是以1为首项,4为公差的等差数列
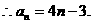 …………6分
…………6分
(II)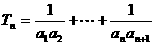

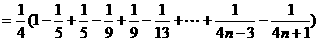
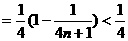 …………10分
…………10分
又易知 单调递增,
单调递增,
故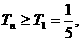
得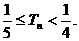 …………12分
…………12分
17.解:(I)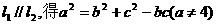
即 …………2分
…………2分
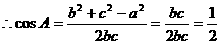
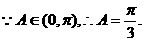 …………5分
…………5分
(II)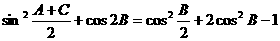
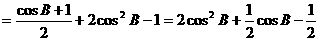
 …………8分
…………8分
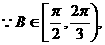
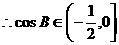 …………9分
…………9分
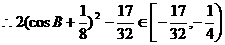 …………11分
…………11分
即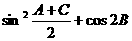 的取值范围为
的取值范围为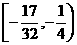 …………12分
…………12分
22.(本题满分14分)
设函数, f(x)=x2-alnx,g(x)=x2-x+m,令F(x)=f(x)-g(x)
(Ⅰ)当m=0,x∈(1,+∞)时,试求实数a的取值范围使得F(x)的图象恒在x轴上方
(Ⅱ)当a=2时,若函数F(x)在[1,3]上恰好有两个不同零点,求实数m的取值范围
(Ⅲ)是否存在实数a的值,使函数f(x)和函数g(x)在公共定义域上具有相同的单调性?若存在,求出a的值,若不存在,说明理由。
[2010淄博一模]答案
21.(本题满分12分)
已知双曲线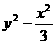 ,的两焦点F1、F2,动点P与F1,F2的距离之和为大于4的定值,且向量
,的两焦点F1、F2,动点P与F1,F2的距离之和为大于4的定值,且向量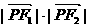 的最大值为9,
的最大值为9,
(1)求动点P的轨迹E的方程
(2)若A、B是曲线E上相异两点,点M(0.-1)满足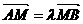 ,求λ的取值范围。
,求λ的取值范围。
20.(本题满分12分)
某校从参加高一年级期中考试的学生中随机抽取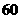 名学 生,将其数学成绩(均为整数)分成六段
名学 生,将其数学成绩(均为整数)分成六段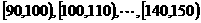 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(I)求分数在[120,130]内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
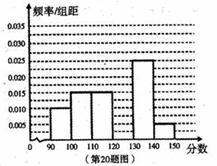 (Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[90,100]记0分,在[110,130]之间记1分,在[130,150)记2分,用ξ表示抽取结束后的总记分,求ξ的分布列和数学期望.
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[90,100]记0分,在[110,130]之间记1分,在[130,150)记2分,用ξ表示抽取结束后的总记分,求ξ的分布列和数学期望.
19.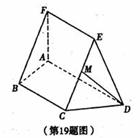 (本小题满分12分)
(本小题满分12分)
如图,在五面体ABCDEF中,FA 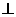 平面ABCD, AD//BC//FE,
平面ABCD, AD//BC//FE,
AB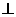 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=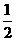 AD
AD
(I)求证:BF⊥DM
(Ⅱ)求二面角A-CD-E的余弦值。
18.(本小题满分12分)
设数列{an}的前n项和为Sn,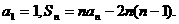
(I)求数列数列{an}的通项公式an,
(II)设数列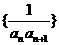 的前n项和为Tn,求证
的前n项和为Tn,求证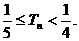
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com