
题目列表(包括答案和解析)
5、已知复数 ,
,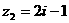 ,则复数
,则复数 的虚部等于________
的虚部等于________
4、直线x+ay+3=0与直线ax+4y+6=0平行的充要条件是__
3、在数列 中,若
中,若 ,
, ,
, ,则该数列的通项为
。
,则该数列的通项为
。
2、命题“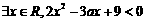 ”为假命题,则实数
”为假命题,则实数 的取值范围为______
的取值范围为______
1、已知向量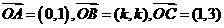 ,若
,若 ,则实数
,则实数 =
=
2.只要注意到 ,即可迅速得到答案.
,即可迅速得到答案.
例14、已知 ,复数
,复数 的实部为
的实部为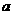 ,虚部为1,则
,虚部为1,则 的取值范围是( )
的取值范围是( )
A.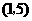 B.
B.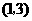 C.
C. D.
D.
[解析]由于0<a<2,故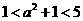 ∴
∴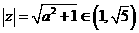 。
。
[答案]C
例15、知复数z=1-i,则 =( )
=( )
A.2i B.-2i C.2 D.-2
[解析]将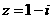 代入得
代入得 ,选B.
,选B.
[答案]B
例16、设z的共轭复数是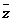 ,或z+
,或z+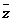 =4,z·
=4,z·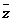 =8,则
=8,则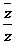 等于( )
等于( )
A.1 B.-i C.±1 D. ±i
[解析] 可设 ,由
,由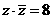 得
得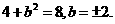

[答案]:D.
例17、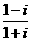 表示为
表示为
 ,则
,则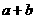 =
。
=
。
[解析] ,因此
,因此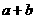 =1。
=1。
[答案]1
例18、若复数z满足z=i(2-z)(i是虚数单位),则z=
[解析]由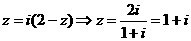 .
.
[答案]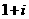
例19、若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b为实数),则b=
A -2
B - C
C  D 2
D 2
[解析](1+bi)(2+i)=(2-b)+(2b+1)i,故2b+1=0,故选B;
[答案]B;
例20、 若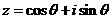 (
( 为虚数单位),则
为虚数单位),则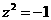 的
的 值可能是
值可能是
A  B
B  C
C  D
D 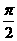
[解析]:把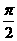 代入验证即得。
代入验证即得。
[答案] D
例21、已知 是实系数一元二次方程
是实系数一元二次方程 的两根,则
的两根,则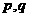 的值为 ( )
的值为 ( )
A、 B、
B、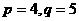 C、
C、 D、
D、
[解析] 因为2+ a i,b+i( i 是虚数单位)是实系数一元二次方程 的两个根,所以a=-1,b=2,所以实系数一元二次方程
的两个根,所以a=-1,b=2,所以实系数一元二次方程 的两个根是
的两个根是 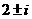 所以
所以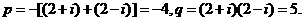
[答案]A
例22、.若复数(1+bi)(2+i)是纯虚数(i是虚数单位,b是实数),则b=
A.-2
B. C.
C. 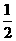 D.2
D.2
[解析]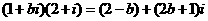 ,依题意
,依题意 ,
选 D .
,
选 D .
[答案]D
例23、已知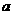 是实数,
是实数,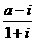 是春虚数,则
是春虚数,则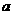 =( )
=( )
(A)1
(B)-1 (C) (D)-
(D)-
[解析]:由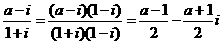 是纯虚数,则
是纯虚数,则 且
且 故
故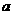 =1.
=1.
[答案]A
例24、复数 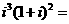 ( )
( )
A.2 B.-2 C.  D.
D. 
[解析]: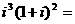
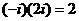
[答案]:A.
例25、若复数(a2-3a+2)+(a-1)i是纯虚数,则实数a的值为( )
A.1 B.2 C.1或2 D.-1
[解析]由 得
得 ,且
,且

[答案]B
例25、若复数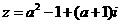 (
( )是纯虚数,则
)是纯虚数,则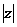 = .2
= .2
[解析]由 ,所以
,所以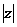 =2.
=2.
[答案].2
例26、.已知zi+z=2,则复数z=()
A.1-i B.1+i C.2i D.-2i
[解析]由zi+z=2得Z=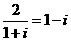 ,所以选A项.
,所以选A项.
[答案]A
例27、.已知i是虚数单位,
 R,且
R,且 是纯虚数,则
是纯虚数,则 等于( )
等于( )
A.1 B.-1 C.i D.-i
[解析]由 =
= 是纯虚数,得m=2,所以
是纯虚数,得m=2,所以 =
= .
.
例28、若z1=a+2i,z2=3-4i,且 为纯虚数,则实数a的值是 ▲ .
为纯虚数,则实数a的值是 ▲ .
[解析] =
= ,则由条件可得3a-8=0,得a=
,则由条件可得3a-8=0,得a= .
.
例29、已知 ,且
,且 (
( 为虚数单位),则z=_______;
为虚数单位),则z=_______;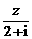 =_______.
=_______.
[解析]设Z=a+bi,则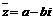 ,所以由条件
,所以由条件 得:
得: 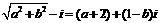 ,所以
,所以 ,即z=2i,
,即z=2i, 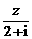 =
= .
.
 [答案]2i,
[答案]2i, .
.
例30、已知复数 ,则
,则 等于( )
等于( )
A.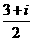 B.
B. C.
C.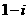 D.
D.
[解析]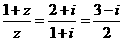 .
.
[答案] D
例30、若 ,则
,则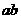 的值是( )。
的值是( )。
A.1 B.0 C.-1 D.-2
[解析]  .
.
[答案]B
例31、已知 的虚部为 (
)
的虚部为 (
)
A.1 B.-1 C. D.
D.
[解析] ,故虚部是1.
,故虚部是1.
[答案]A
 例32、复数
例32、复数 (
( 是虚数单位)在复平面上对应的点位于 ( )
是虚数单位)在复平面上对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[解析] ,所以在第二象限.
,所以在第二象限.
[答案]B
例33、若 (其中
(其中 是虚数单位,b是实数),则b= ( )
是虚数单位,b是实数),则b= ( )
A.-4 B.4 C.-8 D.8
[解析] ,所以b=-8.
,所以b=-8.
例59、若某几何体的三视图(单位: )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是
 .
.
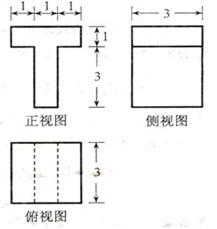 答案:18
答案:18
[解析]该几何体是由二个长方体组成,下面体积为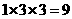 ,上面的长方体体积为
,上面的长方体体积为 ,因此其几何体的体积为18
,因此其几何体的体积为18
例60、如图,在长方形 中,
中, ,
, ,
, 为
为 的中点,
的中点, 为线段
为线段 (端点除外)上一动点.现将
(端点除外)上一动点.现将 沿
沿 折起,使平面
折起,使平面 平面
平面 .在平面
.在平面 内过点
内过点
作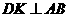 ,
, 为垂足.设
为垂足.设 ,则
,则 的取值范围是
.
的取值范围是
.
答案: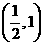
[解析]此题的破解可采用二个极端位置法,即对于F位于DC的中点时, ,随着F点到C点时,因
,随着F点到C点时,因 平面
平面 ,即有
,即有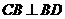 ,对于
,对于 ,又
,又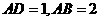 ,因此有
,因此有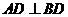 ,则有
,则有 ,因此
,因此 的取值范围是
的取值范围是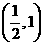 .
.
例62、设 和
和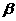 为不重合的两个平面,给出下列命题: (1)若
为不重合的两个平面,给出下列命题: (1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于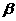 内的两条直线,则
内的两条直线,则 平行于
平行于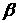 ;(2)若
;(2)若 外一条直线
外一条直线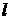 与
与 内的一条直线平行,则
内的一条直线平行,则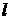 和
和 平行;(3)设
平行;(3)设 和
和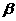 相交于直线
相交于直线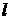 ,若
,若 内有一条直线垂直于
内有一条直线垂直于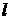 ,则
,则 和
和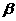 垂直;(4)直线
垂直;(4)直线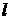 与
与 垂直的充分必要条件是
垂直的充分必要条件是 与
与 内的两条直线垂直。
内的两条直线垂直。
上面命题中,真命题的序号 (写出所有真命题的序号).
[解析] 考查立体几何中的直线、平面的垂直与平行判定的相关定理。真命题的序号是(1)(2)
例63、直三棱柱 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若 ,
, ,则此球的表面积等于
。
,则此球的表面积等于
。
解:在 中
中 ,
, ,可得
,可得 ,由正弦定理,可得
,由正弦定理,可得 外接圆半径r=2,设此圆圆心为
外接圆半径r=2,设此圆圆心为 ,球心为
,球心为 ,在
,在 中,易得球半径
中,易得球半径 ,故此球的表面积为
,故此球的表面积为 .
.
例64、对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。
1相对棱AB与CD所在的直线异面;
2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
[解析]①④⑤
例65、设某几何体的三视图如下(尺寸的长度单位为m)。
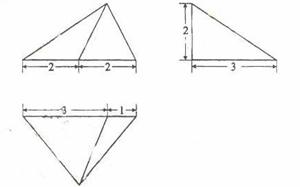 则该几何体的体积为
则该几何体的体积为 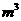
[解析]这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3, 体积等于 ×2×4×3=4
×2×4×3=4
[答案]4
例67、在半径为13的球面上有A , B, C 三点,AB=6,BC=8,CA=10,则
(1)球心到平面ABC的距离为 12 ;
(2)过A,B两点的大圆面为平面ABC所成二面角为(锐角)的正切值为 3
[答案]:(1)12;(2)3
 [解析](1)由
[解析](1)由 的三边大小易知此三角形是直角三角形,所以过
的三边大小易知此三角形是直角三角形,所以过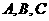 三点小圆的直径即为10,也即半径是5,设球心到小圆的距离是
三点小圆的直径即为10,也即半径是5,设球心到小圆的距离是 ,则由
,则由 ,可得
,可得 。(2)设过
。(2)设过 三点的截面圆的圆心是
三点的截面圆的圆心是 中点是
中点是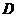 点,球心是
点,球心是 点,则连三角形
点,则连三角形 ,易知
,易知 就是所求的二面角的一个平面角,
就是所求的二面角的一个平面角, ,所以
,所以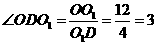 ,即正切值是3。.
,即正切值是3。.
例68、如图是一个几何体的三视图,若它的体积是 ,则
,则 _______
_______
[考点定位]本小题考查三视图、三棱柱的体积,基础题。
解析:知此几何体是三棱柱,其高为3,底面是底边长为2,底边上的高为 的等腰三角形,所以有
的等腰三角形,所以有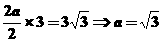 。
。
例69、如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为 。则该集合体的俯视图可以是
。则该集合体的俯视图可以是
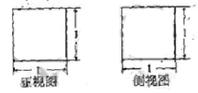

解析 解法1 由题意可知当俯视图是A时,即每个视图是变边长为1的正方形,那么此几何体是立方体,显然体积是1,注意到题目体积是 ,知其是立方体的一半,可知选C.
,知其是立方体的一半,可知选C.
解法2 当俯视图是A时,正方体的体积是1;当俯视图是B时,该几何体是圆柱,底面积是 ,高为1,则体积是
,高为1,则体积是 ;当俯视是C时,该几何是直三棱柱,故体积是
;当俯视是C时,该几何是直三棱柱,故体积是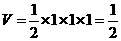 ,当俯视图是D时,该几何是圆柱切割而成,其体积是
,当俯视图是D时,该几何是圆柱切割而成,其体积是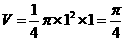 .故选C.
.故选C.
例70、在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;
④每个面都是等边三角形的四面体;
⑤每个面都是直角三角形的四面体.
解析:在正方体ABCD-A1B1C1D1上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是①矩形如ACC1A1;. ③有三个面为等腰直角三角形,有一个面为等边三角形的四面体,如A-A1BD;④每个面都是等边三角形的四面体,如ACB1D1;⑤每个面都是直角三角形的四面体,如AA1DC,所以填①③④⑤。
例73、如图,正方体 的棱长为1,过点A作平面
的棱长为1,过点A作平面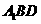 的垂线,垂足为点
的垂线,垂足为点 .
.
有下列四个命题
 A.点
A.点 是
是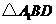 的垂心
的垂心
B. 垂直平面
垂直平面
C.二面角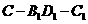 的正切值为
的正切值为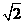
D.点 到平面
到平面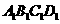 的距离为
的距离为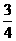
其中真命题的代号是 .(写出所有真命题的代号)
解析:因为三棱锥A-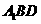 是正三棱锥,故顶点A在底面的射映是底面中心,A正确;面
是正三棱锥,故顶点A在底面的射映是底面中心,A正确;面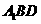 ∥面
∥面 ,而AH垂直平面
,而AH垂直平面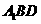 ,所以AH垂直平面
,所以AH垂直平面 ,B正确;
,B正确;
连接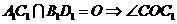 即为二面角
即为二面角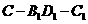 的平面角,
的平面角,
 C正确; 对于D,
连接
C正确; 对于D,
连接 面
面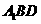 ,故点
,故点 是
是
的三等分点,故点 到平面
到平面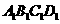 的距离为
的距离为 从而D错.
从而D错.
则应填A,B,C.
例74、若一个底面边长为 ,棱长为
,棱长为 的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .
解析:根据条件正六棱柱的最长的对角线为球的直径,由 得R=
得R= ,球体积为
,球体积为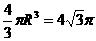
例75、已知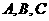 三点在球心为
三点在球心为 ,半径为
,半径为 的球面上,
的球面上, ,且
,且 那么
那么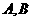 两点的球面距离为_______________,球心到平面
两点的球面距离为_______________,球心到平面 的距离为______________.
的距离为______________.
解:如右图,因为 ,所以AB是截面
,所以AB是截面
的直径,又AB=R,所以△OAB是等边三角形,
所以ÐAOB= ,故
,故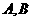 两点的球面距离为
两点的球面距离为 ,
,
于是ÐO1OA=30°,所以球心到平面 的距离
的距离
OO1=Rcos30°=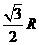 .
.
例76、如图,已知正三棱柱 的底面边长为1,高为8,一质点自
的底面边长为1,高为8,一质点自 点出发,沿着三棱柱的侧面绕行两周
点出发,沿着三棱柱的侧面绕行两周
到达 点的最短路线的长为 .
点的最短路线的长为 .

 解:将正三棱柱
解:将正三棱柱 沿
沿
侧棱CC1展开,其侧面展开图如
图所示,由图中路线可得结论。
例77、若一条直线与一个正四棱柱各个面所成的角都为 ,则
,则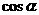 =______
=______
 [解析]不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故
[解析]不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故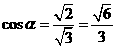 .
.
[点评]本题考查了直线与平面所成角的定义以及正四棱柱的概念,充分考查了转化思想的应用.
 例78、如图,在正三棱柱ABC-
例78、如图,在正三棱柱ABC- 中,所有棱长均为1,则点B
中,所有棱长均为1,则点B 到平面ABC
到平面ABC 的距离为 .
的距离为 .
解:利用等体积法,易知VB1-ABC1= ,
,
所以点B 到平面ABC
到平面ABC 的距离为
的距离为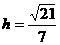
例79、水平桌面α上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球,它和下面4个球恰好都相切,则小球的球心到水平桌面α的距离是
解:水平桌面α上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球,它和下面4个球恰好都相切,5个球心组成一个正四棱锥,这个正四棱锥的底面边长为4R,侧棱长为3R,求得它的高为R,所以小球的球心到水平桌面α的距离是3R.
例80、如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
解:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”;
 例81、
例81、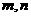 是空间两条不同直线,
是空间两条不同直线,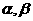 是两个不同平面,下面有四个命题:
是两个不同平面,下面有四个命题:
① ②
②
③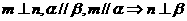 ④
④
其中真命题的编号是 ;(写出所有真命题的编号)
 解析:四个命题:①
解析:四个命题:① ,为真命题;②
,为真命题;② ,为假命题;③
,为假命题;③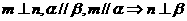 为假命题; ④
为假命题; ④ 为真命题,
为真命题,
所以真命题的编号是①、④.


例23、数列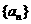 中,
中, 且满足
且满足
(Ⅰ)求数列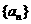 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设 求
求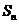 的解析式;
的解析式;
(Ⅲ)设计一个求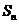 的程序框图.
的程序框图.
[解](Ⅰ)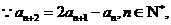
 所以数列
所以数列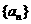 为等差数列. ………………………2分
为等差数列. ………………………2分
又

所以 ……………………………………4分
……………………………………4分
(Ⅱ)令 则有
则有 所以
所以
所以当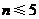 时,
时,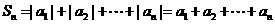
 ……………………6分
……………………6分
当 时,
时,

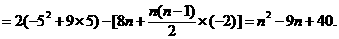 ……………8分
……………8分
 (Ⅲ)
(Ⅲ)
……………………………………………12分
例24、设数列 的前
的前 项和为
项和为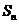 ,点
,点 在直线
在直线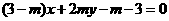 上,
上, 为常数,
为常数,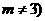 .
.
(Ⅰ)求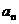 ;(Ⅱ)若数列
;(Ⅱ)若数列 的公比
的公比 ,数列
,数列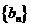 满足
满足 ,求证:
,求证: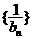 为等差数列,并求
为等差数列,并求 ;(III)设数列
;(III)设数列 满足
满足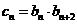 ,
,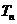 为数列
为数列 的前
的前 项和,且存在实数
项和,且存在实数 满足
满足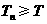 ,
,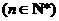 ,求
,求 的最大值.
的最大值.
[解](Ⅰ)由题设,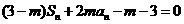 ①…………………1分
①…………………1分

由①, 时,
时, ② ………………2分
② ………………2分
① ②得,
②得,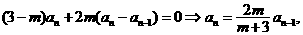
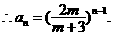 …………………………………………………………………5分
…………………………………………………………………5分
(Ⅱ)由(Ⅰ)知
化简得:  …………………………7分
…………………………7分
 为等差数列,
为等差数列,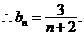 ………………………9分
………………………9分
(III)由(Ⅱ)知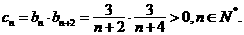
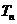 为数列
为数列 的前
的前 项和,因为
项和,因为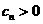 ,
,
所以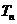 是递增的,
是递增的,  .……………………………………………12分
.……………………………………………12分
所以要满足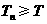 ,
,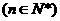 ,
,
所以 的最大值是
的最大值是 .……………………………………………………………………14分
.……………………………………………………………………14分
w. 例25、已知数列{ }中,
}中, 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(1)令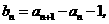 求证数列
求证数列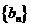 是等比数列(2)求数列
是等比数列(2)求数列
⑶ 设

 的前n项和,是否存在实数
的前n项和,是否存在实数 ,使得数列
,使得数列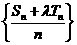 为等差数列?若存在,试求出
为等差数列?若存在,试求出 .若不存在,则说明理由。
.若不存在,则说明理由。
解:(I)由已知得
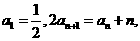

又
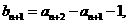

 是以
是以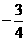 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,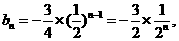

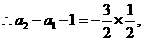
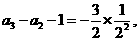


将以上各式相加得: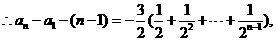


(III)解法一:存在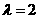 ,使数列
,使数列 是等差数列.
是等差数列.




数列 是等差数列的充要条件是
是等差数列的充要条件是 、
、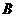 是常数
是常数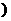 即
即
又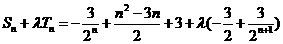

 当且仅当
当且仅当 ,即
,即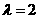 时,数列
时,数列 为等差数列.
为等差数列.
解法二:存在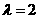 ,使数列
,使数列 是等差数列.由(I)、(II)知,
是等差数列.由(I)、(II)知,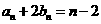


 又
又
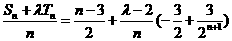
 当且仅当
当且仅当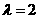 时,数列
时,数列 是等差数列.
是等差数列.
例26、如图, 是曲线
是曲线
 上的
上的 个点,点
个点,点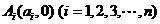 在
在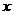 轴的正半轴上,
轴的正半轴上, 是正三角形(
是正三角形( 是坐标原点)
.(Ⅰ) 写出
是坐标原点)
.(Ⅰ) 写出 ;(Ⅱ)求出点
;(Ⅱ)求出点
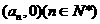 的横坐标
的横坐标 关于
关于 的表达式;
的表达式;
(Ⅲ)设 ,若对任意正整数
,若对任意正整数 ,当
,当 时,不等式
时,不等式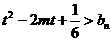 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ) 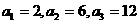 .…………………………………………… 2分
.…………………………………………… 2分
(Ⅱ)依题意 ,则
,则

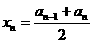 ,
,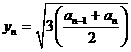 … 3分
… 3分
在正三角形 中,有
中,有
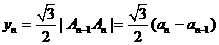 .
. .……………… 4分
.……………… 4分
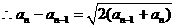 ,
,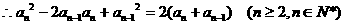 , ①
, ①
同理可得 .
②
.
②
①-②并变形得
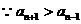 ,
, ,
… 6分
,
… 6分
 . ∴数列
. ∴数列 是以
是以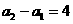 为首项,公差为
为首项,公差为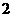 的等差数列.
的等差数列.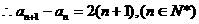 , …………………………………… 7分
, …………………………………… 7分

 ,
,
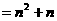 .
.
 .
………………………… 8分
.
………………………… 8分
(Ⅲ)解法1 :∵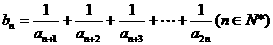 , ∴
, ∴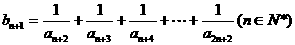 .
.

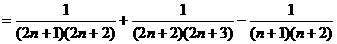
 .∴当
.∴当 时,上式恒为负值,∴当
时,上式恒为负值,∴当 时,
时,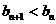 ,
,
∴数列 是递减数列.
是递减数列.
 的最大值为
的最大值为 .
……………… 11分
.
……………… 11分
若对任意正整数 ,当
,当 时,不等式
时,不等式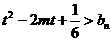 恒成立,则不等式
恒成立,则不等式 在
在 时恒成立,即不等式
时恒成立,即不等式 在
在 时恒成立.
时恒成立.
设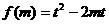 ,则
,则 且
且 ,∴
,∴
解之,得  或
或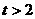 ,即
,即 的取值范围是
的取值范围是 .…………… 14分
.…………… 14分
解法2:∵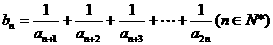 ,
,


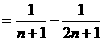
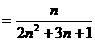 设
设 ,则
,则 .
.
当 时,
时,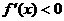 ,
,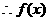 在
在 是增函数.∴数列
是增函数.∴数列 是递减数列.
是递减数列.  的最大值为
的最大值为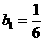 . …… 11分
. …… 11分
(以下解答过程与解法1相同)
例27、已知函数 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与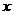 轴的交点为
轴的交点为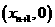 ,其中
,其中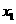 为正实数
(1)用
为正实数
(1)用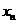 表示
表示 ;(2)
;(2) ,若
,若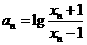 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
(3)若数列
的通项公式;
(3)若数列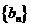 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 项和
项和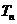 ,求
,求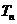 。解:(1)由题可得
。解:(1)由题可得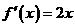 ,所以在曲线上点
,所以在曲线上点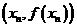 处的切线方程为
处的切线方程为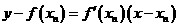 ,即
,即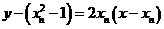 -2分
-2分
令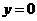 ,得
,得 ,即
,即 由题意得
由题意得 ,所以
,所以 --4分
--4分
(2)因为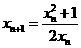 ,所以
,所以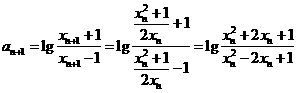

即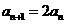 ,所以数列
,所以数列 为等比数列故
为等比数列故 ---8分
---8分
(3)当 时,
时,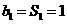 当
当 时,
时,
所以数列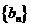 的通项公式为
的通项公式为 ,故数列
,故数列 的通项公式为
的通项公式为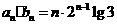
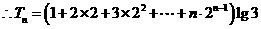 ① ①
① ①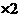 的
的 ②
②
① ②得
②得 故
故 --14分
--14分
例28、


例29、数列 的前
的前 项和为
项和为 ,已知
,已知
(Ⅰ)写出 与
与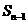 的递推关系式
的递推关系式 ,并求
,并求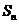 关于
关于 的表达式;
的表达式;
(Ⅱ)设 ,求数列
,求数列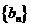 的前
的前 项和
项和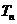 。
。
解:由
 得:
得: ,即
,即 ,所以
,所以 ,对
,对 成立。由
成立。由 ,
, ,…,
,…, 相加得:
相加得: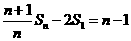 ,又
,又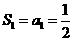 ,所以
,所以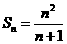 ,当
,当 时,也成立。
时,也成立。
(Ⅱ)由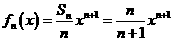 ,得
,得 。而
。而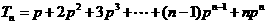 ,
,


例30、已知数列{ }中,
}中, 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令 (Ⅱ)求数列
(Ⅱ)求数列
(Ⅲ)设

 的前n项和,是否存在实数
的前n项和,是否存在实数 ,使得数列
,使得数列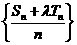 为等差数列?若存在,试求出
为等差数列?若存在,试求出 .若不存在,则说明理由。
.若不存在,则说明理由。
解:(I)由已知得 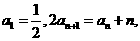

又
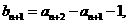

 是以
是以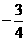 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,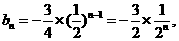

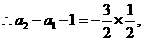
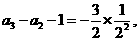

 将以上各式相加得:
将以上各式相加得:
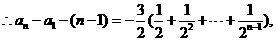


(III)解法一:存在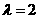 ,使数列
,使数列 是等差数列.
是等差数列.

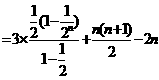
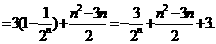

数列 是等差数列的充要条件是
是等差数列的充要条件是 、
、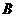 是常数
是常数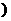 即
即
又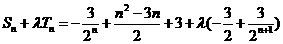

 当且仅当
当且仅当 ,即
,即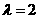 时,数列
时,数列 为等差数列.
为等差数列.
解法二:存在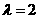 ,使数列
,使数列 是等差数列.
是等差数列.
由(I)、(II)知,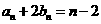


 又
又
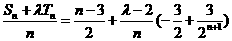
 当且仅当
当且仅当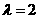 时,数列
时,数列 是等差数列.
是等差数列.
例32、在数列 中,
中, ,其中
,其中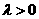 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列 的前
的前 项和
项和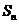 ;(Ⅲ)证明存在
;(Ⅲ)证明存在 ,使得
,使得 对任意
对任意 均成立.
均成立.
(Ⅰ)解法一: ,
, ,
,
 .由此可猜想出数列
.由此可猜想出数列 的通项公式为
的通项公式为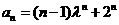 .
.
以下用数学归纳法证明.(1)当 时,
时, ,等式成立.
,等式成立.
(2)假设当 时等式成立,即
时等式成立,即 ,
,
那么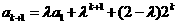

 .
.
就是说,当 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式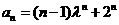 对任何
对任何 都成立.
都成立.
解法二:由 ,
,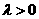 ,可得
,可得 ,
,
所以 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故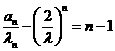 ,所以数列
,所以数列 的通项公式为
的通项公式为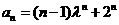 .
.
(Ⅱ)解:设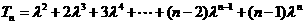 , ①
, ①
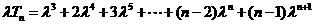 ②
②
当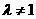 时,①式减去②式,得
时,①式减去②式,得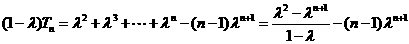 ,
,
 .这时数列
.这时数列 的前
的前 项和
项和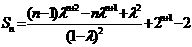 .当
.当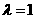 时,
时, .这时数列
.这时数列 的前
的前 项和
项和 .
.
(Ⅲ)证明:通过分析,推测数列 的第一项
的第一项 最大,下面证明:
最大,下面证明:
 . ③由
. ③由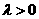 知
知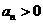 ,要使③式成立,只要
,要使③式成立,只要 ,
,
因为

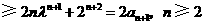 .所以③式成立.
.所以③式成立.
因此,存在 ,使得
,使得 对任意
对任意 均成立.
均成立.
例33、已知数列 中
中 ,
,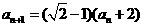 ,
, .
.
(Ⅰ)求 的通项公式;(Ⅱ)若数列
的通项公式;(Ⅱ)若数列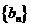 中
中 ,
,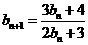 ,
, ,
,
证明: ,
, .
.
解:(Ⅰ)由题设: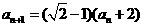

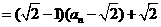 ,
,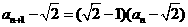 .
.
所以,数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,
,
即 的通项公式为
的通项公式为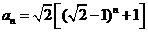 ,
, .
.
(Ⅱ)用数学归纳法证明.(ⅰ)当 时,因
时,因 ,
, ,所以
,所以
 ,结论成立.(ⅱ)假设当
,结论成立.(ⅱ)假设当 时,结论成立,即
时,结论成立,即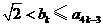 ,
,
也即 .当
.当 时,
时,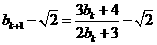

 ,又
,又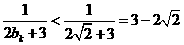 ,
,
所以 

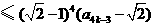
 .
.
也就是说,当 时,结论成立.
时,结论成立.
根据(ⅰ)和(ⅱ)知 ,
, .
.
例34、数列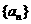 为等差数列,
为等差数列, 为正整数,其前
为正整数,其前 项和为
项和为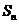 ,数列
,数列 为等比数列,且
为等比数列,且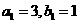 ,数列
,数列 是公比为64的等比数列,
是公比为64的等比数列, .(1)求
.(1)求 ;(2)求证
;(2)求证 .
.
解:(1)设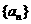 的公差为
的公差为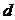 ,
, 的公比为
的公比为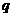 ,则
,则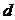 为正整数,
为正整数, ,
,
依题意有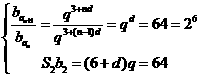 ①由
①由 知
知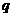 为正有理数,故
为正有理数,故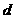 为
为 的因子
的因子 之一,
之一,
解①得 故
故
(2) ∴
∴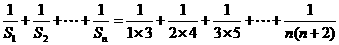

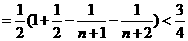
例35、 数列
(Ⅰ)求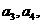 并求数列
并求数列 的通项公式;
的通项公式;
(Ⅱ)设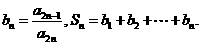 证明:当
证明:当
解: (Ⅰ)因为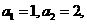 所以
所以

一般地,当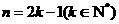 时,
时, =
= ,即
,即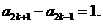
所以数列 是首项为1、公差为1的等差数列,因此
是首项为1、公差为1的等差数列,因此
当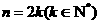 时,
时,
所以数列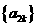 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此 故数列
故数列 的通项公式为
的通项公式为
(Ⅱ)由(Ⅰ)知,
 ①
①
 ②
②
①-②得,
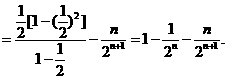
所以
要证明当 时,
时,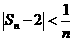 成立,只需证明当
成立,只需证明当 时,
时, 成立.
成立.
证法一(1)当n = 6时,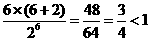 成立.
成立.
(2)假设当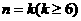 时不等式成立,即
时不等式成立,即
则当n=k+1时,
由(1)、(2)所述,当n≥6时, .即当n≥6时,
.即当n≥6时,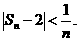
证法二 令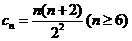 ,则
,则
所以当 时,
时, .因此当
.因此当 时,
时, 于是当
于是当 时,
时,
综上所述,当 时,
时,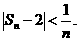
例36、已知数列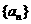 的首项
的首项 ,
, ,
,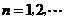 .
.
(Ⅰ)求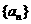 的通项公式;(Ⅱ)证明:对任意的
的通项公式;(Ⅱ)证明:对任意的 ,
,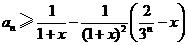 ,
,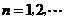 ;
;
(Ⅲ)证明:试题详情
(Ⅱ)
 (3)
(3)
 (4)
(4)
22.(1).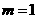 ,椭圆
,椭圆 的方程:
的方程: ;(2).
;(2). .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com