11.指出下列命题是全称命题还是特称命题,并判断真假.

(1)对任意a＞0且a≠1,y＝a^x的图象恒在x轴上方;

(2)对任意实数x₁,x₂,若x₁＜x₂,则tanx₁＜tanx₂;

(3)T∈R,使|sin(x+T)|＝|sinx|;

(4)x∈R,使x²+1＜0.

解:(1)(2)是全称命题,(3)(4)是特称命题.

(1)∵a^x＞0(a＞0,a≠1)恒成立,

∴命题(1)是真命题.

(2)存在x₁＝0,x₂＝π,x₁＜x₂,但tan0＝tanπ,

∴命题(2)是假命题.

(3)y＝|sinx|是周期函数,π就是它的一个周期,

∴命题(3)是真命题.

(4)对任意x∈R,x²+1＞0,

∴命题(4)是假命题.

10.若R(x):sinx+cosx＞m,s(x):x²+mx+1＞0,如果对x∈R,R(x)为假命题且s(x)为真命题,求实数m的取值范围.

解:由于sinx+cosx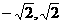＝∈［］,如果对任意的x∈R,r(x)为假命题,即对任意的x∈R,不等式sinx+cosx＞m恒不成立,则m≥.又对任意的x∈R,s(x)为真命题,即对任意的x∈R,不等式x²+mx+1＞0恒成立,所以Δ＝m²-4＜0,即-2＜m＜2.故如果对任意的x∈R,r(x)为假命题且s(x)为真命题,应有≤m＜2.

9.把下面不完整的命题补充完整,并使之成为真命题,若函数f(x)＝3+log₂x的图象与g(x)的图象关于______________对称,则函数g(x)＝______________.(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)

解析:运用函数图象关于x轴(或y轴或原点或直线y＝x)等对称原理可得出相应答案,本题是一个开放性问题.

方法一:将y＝f(x)中的y用-y代替,即得关于x轴对称的图象的解析式;将y＝f(x)中的x用-x代替,得关于y轴对称的图象的解析式;将y＝f(x)中的x,y对换,得关于直线y＝x对称的图象的解析式.

方法二:设点P(x₀,y₀)在f(x)的图象上,P关于x轴的对称点为M(x,y),则y₀＝f(x),　　　　　 ①

x₀＝x,y₀＝-y,　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　②

把②代入①,得y＝-f(x)＝-3-log₂x.(其余情况仿此解之,学生自己完成)

答案:x轴 -3-log₂x

8.下列三种说法:

①命题“x∈R,使得x²+1＞3x”的否定是“x∈R,都有x²+1≤3x”;

②设p、q是简单命题,若“p∨q”为假命题,则“p∧q”为真命题;

③把函数y＝sin(-2x)(x∈R)的图象上所有的点都向右平移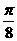个单位即可得到函数y＝sin()(x∈R)的图象.其中正确说法的序号是_________.

解析:本题考查了存在性命题的否定写法,真值表的应用,以及三角函数的图象及其性质.

答案:①②③

7.设数列{a_n}的前n项和为S_n(n∈N^*),关于数列{a_n}有下列三个命题:

①若{a_n}既是等差数列又是等比数列,则a_n＝a _n+1(n∈N^*);

②若S_n＝an²+bn(a,b∈R),则{a_n}为等差数列;

③若S_n＝1-(-1)ⁿ,则{a_n}是等比数列.

这些命题中正确命题的序号是__________.

解析:说明命题为真命题需证明,说明一个命题为假命题,只需举一个反例,主要考查判断命题真假的方法.

(1)∵{a_n}为等差数列,设公差为d,则由题意a_n-d、a_n、a_n+d为等比数列,

∴a_n²＝(a_n-d)(a_n+d).∴d＝0.

∴①正确.

(2)当n＝1时,a₁＝S₁＝a+b;当n≥2时,a_n＝S_n-S_n-1＝2an-a+b;∵n＝1适合上式,

∴a_n＝2an-a+b.

而a _n+1-a_n＝2a(常数),∴{a_n}为等差数列.

∴②正确.

(3)同(2)得a_n＝(-1)^n-1·2,而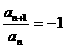(常数),∴{a_n}是等比数列.∴③正确.

答案:①②③

6.给出下列三个命题:①各侧面都是正方形的棱柱一定是正棱柱;②若直线l⊥平面α,l∥平面β,则α⊥β;③命题“异面直线a,b不垂直,则过a的任一平面与b都不垂直”的否命题.其中正确的命题是(　　 )

A.②　　　 　　　　　　　B.①③　　　　 　　　　　　C.①②　　 　　　　　　　D.②③

解析:此类题目应对所给命题逐个判断,若是真命题,给出简单推论,若是假命题,只要举出反例即可,对于①,若底面为菱形,则不是正棱柱;对于③,其命题的否命题为异面直线a,b垂直,则过a的任一平面与b都垂直,明显是假命题,综上所述,只有②是正确的命题,故选A.

答案:A

5.下列特称命题中,真命题的个数是(　　 )

①存在一个实数a,使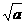为正整数

②存在一个实数x,使为正整数

③存在一个实数y,使为整数

A.0　　　 　　　　　　　　B.1 　　　　　　　　　　C.2　　　 　　　　　　　　　D.3

解析:对于①,当a＝4时, 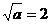为正整数;对于②,当x＝1时, 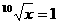为正整数;对于③,当y＝1时,为整数,故选D.

答案:D

4.设α,β为两个不同的平面,l、m为两条不同的直线,且lα,mβ,有如下两个命题:①若α∥β,则l∥m;②若l⊥m,则α⊥β,那么(　　 )

A.①是真命题,②是假命题　　　　　　　　　　　　　　　　　 B.①是假命题,②是真命题

C.①②都是真命题　　　　　　　　　　　　　　　　　　　　　 D.①②都是假命题

解析:①若α∥β,直线l和m可以平行,也可以异面,②若l⊥m,l与m可以异面垂直,此时平面α可以与平面β平行,故选D.

答案:D

3.给出如下三个命题:

①四个非零实数a,b,c,d依次成等比数列的充要条件是ad＝bc;

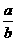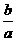②设a,b∈R,且ab≠0,若＜1,则＞1;

③若f(x)＝log₂x,则f(|x|)是偶函数.

其中不正确的命题是(　　 )

A.①②③　　　 　　　　　B.①②　 　　　　　　　　C.②③　　 　　　　　　　D.①③

解析:对于①,可举反例,如a,b,c,d依次取值为1,4,2,8,故①错;对于②,可举反例,如a,b异号,虽然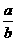＜1,但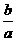＜0,故②错;对于③,y＝f(|x|)＝log₂(|x|),显然y＝f(|x|)为偶函数,故③正确,选B.

答案:B

2.下列全称命题中,真命题的个数是(　　 )

①任意的指数函数都是单调函数

②任意的对数函数都是单调函数

③对任意实数a,b,不等式|a|-|b|≤|a-b|成立

A.0　 　　　　　　　　B.1 　　　　　　　　　　C.2　　 　　　　　　　　　D.3

解析:由全称命题的真假判断方法的运用知①②③都正确,故选D.

答案:D