9.已知集合A＝{-1,3,m},集合B＝{3,4},若BA,则实数m＝_____________.

解析:∵集合A＝{-1,3,m},B＝{3,4},

当BA时,实数m＝4.

答案:4

8.(2008重庆高考,理11)设集合U＝{1,2,3,4,5},A＝{2,4},B＝{3,4,5},C＝{3,4},则(A∪B)∩(C)＝__________________.

解析:∵A∪B＝{2,3,4,5},C＝{1,2,5},(A∪B)∩(C)＝{2,5}.

答案:{2,5}

7.设集合M＝{x|x≤m},N＝{y|y＝2^-x,x∈R},若M∩N≠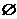,则实数m的取值范围是(　　 )

A.m≥0　　 　　　　　　　B.m＞0 　　　　　　　　C.m≤0　　 　　　　　　　D.m＜0

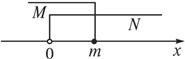
解析:由题意,知集合N＝{y|y＞0},借助数轴可知m＞0.

答案:B

6.设全集U＝R,A＝{x∈N|1≤x≤10},B＝{x∈R|x²+x-6＝0},则右图中阴影表示的集合为(　　 )

A.{2}　　　　　 　　　　　B.{3}　 　　　　　　　C.{-3,2}　　　　　　　　　 D.{-2,3}

解析:题图中阴影部分表示为A∩B,因为A＝{1,2,3,4,5,6,7,8,9,10},集合B＝{-3,2},

所以A∩B＝{2}.

答案：A

5.设a、b∈R,集合{1,a+b,a}＝{0,,b},则b-a等于(　　 )

A.1　　　　 　　　　　B.-1 　　　　　　　　　　　　C.2　　 　　　　　　　　　D.-2

解析:∵a、b∈R,集合{1,a+b,a}＝{0,,b},

∵a≠0,∴a+b＝0,a＝-b.

∴.

∴a＝-1,b＝1.则b-a＝2,故选C.

答案:C

4.(2008江西高考,2)定义集合运算:A*B＝{z|z＝xy,x∈A,y∈B},设A＝{1,2},B＝{0,2},则集合A*B的所有元素之和为(　　 )

A.0　　　　　　　　　 B.2 　　　　　　　　　　　　　C.3　　　 　　　　　　　　D.6

解析:由定义,知A*B＝{0,2,4},故元素之和为6.

答案:D

3.(2008安徽高考,理2)集合A＝{y∈R|y＝lgx,x＞1},B＝{-2,-1,1,2},则下列结论中正确的是(　　 )

A.A∩B＝{-2,-1}　　 B.(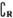A)∪B＝(-∞,0)　　　 C.A∪B＝(0,+∞)　　　 D.(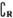A)∩B＝{-2,-1}

解析:∵x＞1,∴y＝lgx＞0.

∴A＝{y∈R|y＞0},(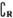A)＝{y|y≤0},

又B＝{-2,-1,1,2},

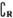∴(A)∩B＝{-2,-1},故选D.

答案:D

2.(2008陕西高考,理2)已知全集U＝{1,2,3,4,5},集合A＝{x|x²-3x+2＝0},B＝{x|x＝2a,a∈A},则集合(A∪B)中元素的个数为(　　 )

A.1　　　 　　　　　　　　B.2 　　　　　　　　　　C.3　　　　 　　　　　　D.4

解析:由题意,知A＝{1,2},B＝{2,4},

∴A∪B＝{1,2,4}.

∴(A∪B)＝{3,5}.

答案:B

1.若A、B、C为三个集合,A∪B＝B∩C,则一定有…(　　 )

A.AC　　　 　　　　　B.CA　　　 　　　　　　C.A≠C　　 　　　　　　　D.A＝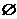

解析:因为AA∪B且B∩CC,A∪B＝B∩C,

由题意,得AC,所以选A.

答案:A

12.已知a＞0且a≠1.设P:关于x的不等式a^x＞1的解集是{x|x＜0},Q:函数y＝lg(ax²-x+a)的定义域为R,如果P和Q有且仅有一个正确,求a的取值范围.

解:若P真,则0＜a＜1;若P假,则a≥1,若Q真,由

得a＞;若Q假,则0＜a≤.

又P和Q有且仅有一个正确,当P真Q假时,0＜a≤;当P假Q真时,a≥1.

综上,得a∈(0,］∪［1,+∞).