
题目列表(包括答案和解析)
20、解:(1)当 时,
时,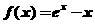 ,
,
∴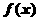 在
在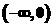 上单调减,在
上单调减,在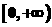 上单调增.
上单调增.
∴ ,
………5分
,
………5分
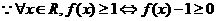 成立,
成立,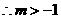 ………7分
………7分
(2)当 时,
时,
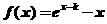 ,
, 在
在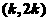 上恒成立. …9分
上恒成立. …9分
∴ 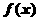 在
在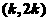 上单调增.(且连续)
上单调增.(且连续)
且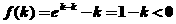 ,…………10分
,…………10分
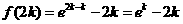

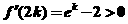 ,
, 在
在 时单调增,∴
时单调增,∴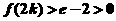 ………13分
………13分
∴由零点存在定理知,函数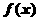 在
在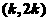 内存在零点.
…………14分
内存在零点.
…………14分
20.(本小题满分14分)已知函数
(1)当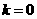 时,若函数
时,若函数 的定义域是R,求实数
的定义域是R,求实数 的取值范围;
的取值范围;
(2)试判断当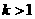 时,函数
时,函数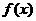 在
在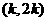 内是否存在零点.
内是否存在零点.
22.(本小题满分14分)
 如图,A为椭圆
如图,A为椭圆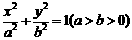 上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
(Ⅰ) 求椭圆的离心率;
(Ⅱ) 设 .
.
①当A点恰为椭圆短轴的一个端点时,
求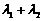 的值;
的值;
②当A点为该椭圆上的一个动点时,试判断是
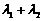 否为定值?若是,请证明;若不是,请说明理由.
否为定值?若是,请证明;若不是,请说明理由.
解(Ⅰ)设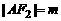 ,则
,则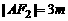 .由题设及椭圆定义得
.由题设及椭圆定义得
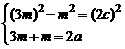 ,消去
,消去 得
得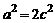 ,所以离心率
,所以离心率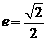 .―――――――3分
.―――――――3分
(Ⅱ)解法一:
由(1)知,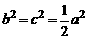 ,所以椭圆方程可化为
,所以椭圆方程可化为 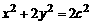 .
.
①当A点恰为椭圆短轴的一个端点时,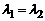 ,直线
,直线 的方程为
的方程为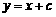 .
.
由 得
得  ,解得
,解得 ,
,
∴ 点 的坐标为
的坐标为 .
.
又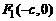 ,所以
,所以 ,
,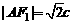 ,所以
,所以 ,
,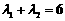 .―――6分
.―――6分
②当A点为该椭圆上的一个动点时,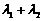 为定值6.
为定值6.
证明 设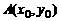 ,
, ,则
,则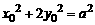 .
.
若 为椭圆的长轴端点,则
为椭圆的长轴端点,则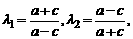 或
或 ,
,
所以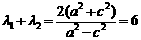 .――――――――――――――――――――――8分
.――――――――――――――――――――――8分
若 为椭圆上异于长轴端点的任意一点,则由
为椭圆上异于长轴端点的任意一点,则由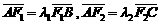 得,
得,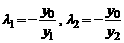 ,所以
,所以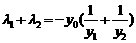 .
.
又直线 的方程为
的方程为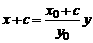 ,所以由
,所以由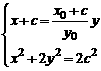 得
得
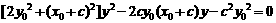 .
.
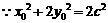 ,
,
∴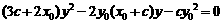 .
.
由韦达定理得  ,所以
,所以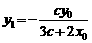 . 同理
. 同理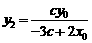 .
.
∴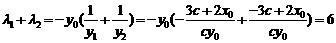 .
.
综上证得,当A点为该椭圆上的一个动点时,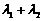 为定值6.―――――――14分
为定值6.―――――――14分
解法二:设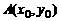 ,
, ,则
,则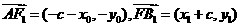
∵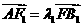 ,∴
,∴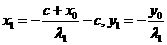 ;………………8分
;………………8分
又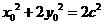 ①,
①,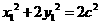 ②,将
②,将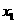 、
、 代入②得:
代入②得:
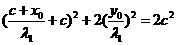 即
即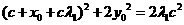 ③;
③;
③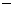 ①得:
①得: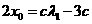 ;……………12分
;……………12分
同理:由 得
得 ,∴
,∴
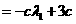 ,∴
,∴ .…14分
.…14分
21.(本小题满分12分)
设函数
(1)证明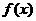 有两个不同的极值点
有两个不同的极值点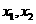 ;
;
(2)对于⑴中的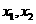 ,若不等式
,若不等式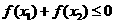 成立,求
成立,求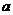 的取值范围.
的取值范围.
解(1)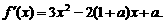 ……………1分
……………1分
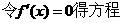 :
: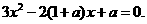
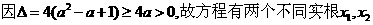 ,…………3分
,…………3分
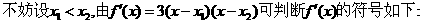
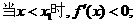
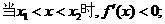
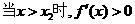
因此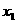 是极大值点,
是极大值点,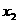 是极小值点.…………………6分
是极小值点.…………………6分
(II)因 :
: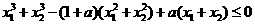 ,
,
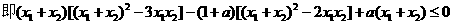 ………8分
………8分
又由(I)知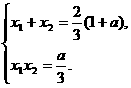 ……………………10分
……………………10分
代入前面不等式,两边除以(1+a),并化简得

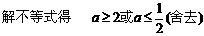
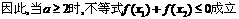 .……………12分
.……………12分
20.(本小题满分12分)
已知数列 是等比数列,
是等比数列, ,如果
,如果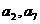 是关于
是关于 的方程:
的方程: 两个实根,(
两个实根,( 是自然对数的底数)
是自然对数的底数)
(1)求 的通项公式;
的通项公式;
(2)设: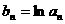 ,
,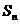 是数列
是数列 的前
的前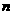 项的和,当:
项的和,当: 时,求
时,求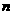 的值;
的值;
(3)对于(2)中的 ,设:
,设: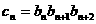 ,而
,而 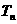 是数列
是数列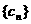 的前
的前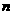 项和,求
项和,求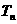 的最大值,及相应的
的最大值,及相应的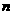 的值。
的值。
解:(1)由于
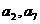 是已知方程的两根,所以,有:
是已知方程的两根,所以,有: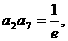 即:
即: 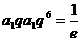 ,
,
而: ,得
,得 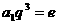 两式联立得:
两式联立得: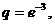 所以,
所以,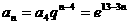
故 得数列 的通项公式为:
的通项公式为: 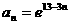 ……………………………………4分
……………………………………4分
(2)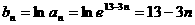 ,所以,数列
,所以,数列 是等差数列,由前
是等差数列,由前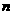 项和公式得:
项和公式得:
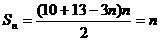 ,得
,得 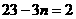 ,所以有:
,所以有: 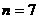 ………………7分
………………7分
(3)由于  得:
得: 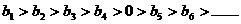 又因为
又因为
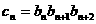 ,所以有:
,所以有: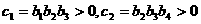 , 而
, 而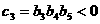
 且 当:
且 当: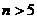 时,都有
时,都有 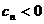 ,但是,
,但是,
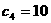 即:
即: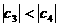 所以,只有当:
所以,只有当: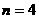 时,
时,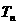 的值最大,此时
的值最大,此时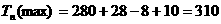 ………………………………………12分
………………………………………12分
21.(Ⅰ)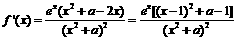 ………………3分
………………3分
⑴ 当 时,
时,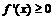 恒成立,
恒成立,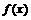 在
在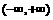 上是增函数;
上是增函数;
⑵ 当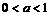 时,令
时,令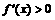 ,即
,即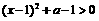 ,解得
,解得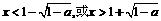 .
.
因此,函数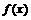 在区间
在区间  内单调递增,在区间
内单调递增,在区间 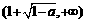 内也单调递增.
内也单调递增.
令 ,解得
,解得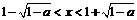 .
.
因此,函数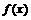 在区间
在区间 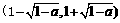 内单调递减. ………………8分
内单调递减. ………………8分
(Ⅱ)当 时,函数
时,函数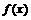 取得极值,即
取得极值,即 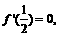
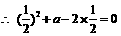 ,
,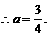
由(Ⅰ)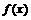 在
在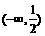 单调递增,在
单调递增,在 单调递减,
单调递减,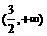 单调递增.
单调递增.
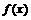 在
在 时取得极大值
时取得极大值 ;
;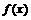 在
在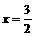 时取得极小值
时取得极小值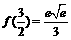 ,
,
故在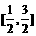 上,
上,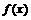 的最大值是
的最大值是 ,最小值是
,最小值是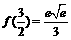 ;
;
对于任意的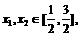
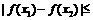
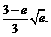 ………………14分
………………14分
21.(本小题满分14分)
设 ,函数
,函数 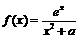 .
.
(Ⅰ)求函数 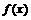 的单调区间;
的单调区间;
(Ⅱ)当 时,函数
时,函数 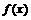 取得极值,证明:对于任意的
取得极值,证明:对于任意的 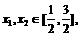
 .
.
20.(Ⅰ)由 得
得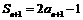 ,相减得:
,相减得: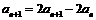 ,∴
,∴ 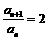
又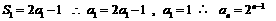 ………………5分
………………5分
(Ⅱ)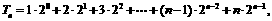 ①
①
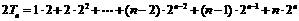 ,②
,②
①-②得 ,
,
则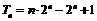 . ………………9分
. ………………9分
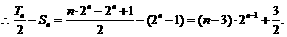
当n=1时,
即当n=1或2时,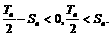
当n>2时,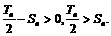 ……………13分
……………13分
20. (本小题满分13分)
设数列 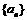 的前项和为
的前项和为 ,且
,且  .
.
(I)求数列 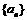 的通项公式;
的通项公式;
(Ⅱ)设数列 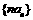 的前n项和为
的前n项和为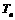 ,对任意
,对任意 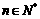 ,比较
,比较 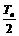 与
与  的大小.
的大小.
19.(Ⅰ)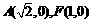 .椭圆
.椭圆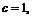
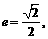 ,
,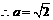 ,
,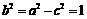 ,
,
 .
………………5分
.
………………5分
(Ⅱ)设点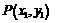 ,过点的圆的切线方程为
,过点的圆的切线方程为 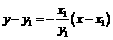 即
即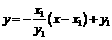 。
。
由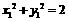 得
得 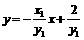 ,令
,令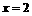 得
得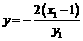 ,故点
,故点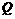

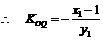 ,又
,又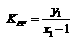
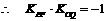
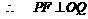 .
………………………………12分
.
………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com