
题目列表(包括答案和解析)
2.复数z= 在复平面上对应的点位于 [A]
在复平面上对应的点位于 [A]
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
1.集合A={x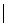 -1≤x≤2},B={x
-1≤x≤2},B={x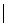 x<1},则A∩B= [D]
x<1},则A∩B= [D]
(A){x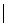 x<1} (B){x
x<1} (B){x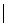 -1≤x≤2}
-1≤x≤2}
(C) {x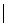 -1≤x≤1}
(D) {x
-1≤x≤1}
(D) {x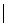 -1≤x<1}
-1≤x<1}
21.本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵
 ,
,
 ,且
,且
 。
。
(Ⅰ)求实数 的值; (Ⅱ)求直线
的值; (Ⅱ)求直线 在矩阵
在矩阵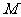 所对应的线性变换作用下的像的方程。
所对应的线性变换作用下的像的方程。
(2)(本小题满分7分)选修4-4分:坐标系与参数方程
在直角坐标系 中,直线
中,直线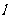 的参数方程为
的参数方程为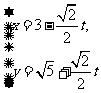 (
( 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为 。
。
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设圆 与直线
与直线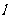 交于点
交于点 .若点
.若点 的坐标为(3,
的坐标为(3, ),求
),求 .
.
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数 (
( )=
)= .
.
(Ⅰ)若不等式 (
( )≤3的解集为{
)≤3的解集为{ -1≤
-1≤ ≤5},求实数
≤5},求实数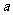 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若 (
( )+
)+ (
( )≥
)≥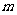 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数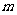 的取值范围。
的取值范围。
20.(本小题满分14分)
(1)已知函数f(x)=x3=x,其图像记为曲线C.
(i)求函数f(x)的单调区间;
(ii)证明:若对于任意非零实数x1,曲线C与其在点P1(x1,f(x1)处的切线交于另一点P2(x2,f(x2).曲线C与其在点P2处的切线交于另一点P3 (x3 f(x3)),线段P1P2,P2P3与曲线C所围成封闭图形的面积分别记为S1,S2,则 为定值:
为定值:
(Ⅱ)对于一般的三次函数g(x)=ax3+bx2+cx+d(a 0),请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
0),请给出类似于(Ⅰ)(ii)的正确命题,并予以证明。
19.(本小题满分13分)
某港口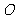 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口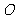 北偏西30°且与该港口相距20海里的
北偏西30°且与该港口相距20海里的 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。
18.(本小题满分13分 )
 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
(I)证明:平面A1ACC1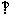 平面B1BCC1;
平面B1BCC1;
(II)设AB=AA1,在圆柱OO1内随机选取一点,记该点取自三棱柱ABC-A1B1C1内的概率为p。
(i)当点C在圆周上运动时,求p的最大值;
(ii)圭亚那平面A1ACC1与平面B1OC所成的角为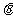 (
( )。当p取最大值时,求cos
)。当p取最大值时,求cos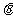 的值。
的值。
17. (本小题满分13分 )
已知在坐标原点O的椭圆C经过点A(2 , 3),且点F(2 ,0)为其右焦点。
(I)求椭圆C的方程;
(II)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由。
16.(本小题满分13分 )
设S是不等式 的解集,m,n
的解集,m,n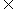 S。
S。
(I)记“使得m + n = 0 成立的有序数组(m , n)”为事件A,试列举A包含的基本事件;
(II)设 =
= ,求
,求 的分布列及其数学期望
的分布列及其数学期望 。
。
15. 已知定义域为(0,+  )的函数f(x)满足:(1)对任意x
)的函数f(x)满足:(1)对任意x 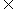 (0,+
(0,+  ),恒有f(2x)=2f(x)成立;(2)当x
),恒有f(2x)=2f(x)成立;(2)当x 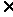 (1,2]时,f(x)=2-x 。给出如下结论:
(1,2]时,f(x)=2-x 。给出如下结论:
①对任意m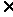 Z,有f(
Z,有f( )= 0;
②函数f(x)的值域为[0, +
)= 0;
②函数f(x)的值域为[0, +  ]; ③ 存在n
]; ③ 存在n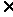 Z,使得f(
Z,使得f( )=9;④“函数f(x)在区间(a、b)上单调递减”的充要条件是“存在k
)=9;④“函数f(x)在区间(a、b)上单调递减”的充要条件是“存在k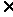 Z,使得(a、b)
Z,使得(a、b) ”。
”。
其中所有正确结论的序号是 。
14.已知函数f(x)=3sin 和g(x)=2cos(
和g(x)=2cos( )+1的图象的对称轴完全相同。若x
)+1的图象的对称轴完全相同。若x 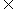 [0,
[0, ],则f(x)的取值范围是
。
],则f(x)的取值范围是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com