
题目列表(包括答案和解析)
8.(2010上海文数)动点 到点
到点 的距离与它到直线
的距离与它到直线 的距离相等,则
的距离相等,则 的轨迹方程为 y2=8x 。
的轨迹方程为 y2=8x 。
解析:考查抛物线定义及标准方程
定义知 的轨迹是以
的轨迹是以 为焦点的抛物线,p=2所以其方程为y2=8x
为焦点的抛物线,p=2所以其方程为y2=8x
(2010浙江理数)(13)设抛物线 的焦点为
的焦点为 ,点
,点
 .若线段
.若线段 的中点
的中点 在抛物线上,则
在抛物线上,则 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。
解析:利用抛物线的定义结合题设条件可得出p的值为 ,B点坐标为(
,B点坐标为( )所以点B到抛物线准线的距离为
)所以点B到抛物线准线的距离为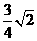 ,本题主要考察抛物线的定义及几何性质,属容易题
,本题主要考察抛物线的定义及几何性质,属容易题
(2010全国卷2理数)(15)已知抛物线 的准线为
的准线为 ,过
,过 且斜率为
且斜率为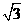 的直线与
的直线与 相交于点
相交于点 ,与
,与 的一个交点为
的一个交点为 .若
.若 ,则
,则 .
.
[答案]2
[命题意图]本题主要考查抛物线的定义与性质.
[解析]过B作BE垂直于准线 于E,∵
于E,∵ ,∴M为中点,∴
,∴M为中点,∴ ,又斜率为
,又斜率为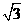 ,
, ,∴
,∴ ,∴
,∴ ,∴M为抛物线的焦点,∴
,∴M为抛物线的焦点,∴ 2.
2.
(2010全国卷2文数)(15)已知抛物线C:y2=2px(p>0)的准线l,过M(1,0)且斜率为 的直线与l相交于A,与C的一个交点为B,若
的直线与l相交于A,与C的一个交点为B,若 ,则p=_________
,则p=_________
[解析]2:本题考查了抛物线的几何性质
设直线AB: ,代入
,代入 得
得 ,又∵
,又∵  ,∴
,∴  ,解得
,解得 ,解得
,解得 (舍去)
(舍去)
2. (2010江苏卷)9、在平面直角坐标系xOy中,已知圆 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是______▲_____[来源
上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是______▲_____[来源
[解析]考查圆与直线的位置关系。 圆半径为2,
圆心(0,0)到直线12x-5y+c=0的距离小于1, ,
, 的取值范围是(-13,13)。
的取值范围是(-13,13)。
12. .设圆心为
.设圆心为 ,则
,则 ,解得
,解得 .
.
(2010四川文数)(14)直线 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 .
.
解析:方法一、圆心为(0,0),半径为2


 w_w w. k#s5_
w_w w. k#s5_
圆心到直线 的距离为d=
的距离为d=
故
得|AB|=2
答案:2
(2010山东理数)

[解析]由题意,设所求的直线方程为 ,设圆心坐标为
,设圆心坐标为 ,则由题意知:
,则由题意知:
 ,解得
,解得 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以 ,故圆心坐标为(3,0),因为圆心(3,0)在所求的直线上,所以有
,故圆心坐标为(3,0),因为圆心(3,0)在所求的直线上,所以有 ,即
,即 ,故所求的直线方程为
,故所求的直线方程为 。
。
[命题意图]本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
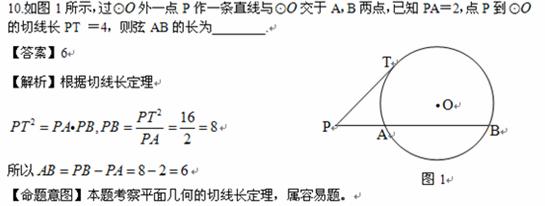
(2010湖南理数)
12.(2010广东理数)已知圆心在x轴上,半径为 的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
14.(2010湖南文数)若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线l的斜率为 -1 ,圆(x-2)2+(y-3)2=1关于直线对称的圆的方程为 
(2010全国卷2理数)(16)已知球 的半径为4,圆
的半径为4,圆 与圆
与圆 为该球的两个小圆,
为该球的两个小圆, 为圆
为圆 与圆
与圆 的公共弦,
的公共弦, .若
.若 ,则两圆圆心的距离
,则两圆圆心的距离
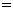 .
.
[答案]3
[命题意图]本试题主要考查球的截面圆的性质,解三角形问题.
[解析]设E为AB的中点,则O,E,M,N四点共面,如图,∵ ,所以
,所以 ,∴
,∴ ,由球的截面性质,有
,由球的截面性质,有 ,∵
,∵ ,所以
,所以 与
与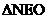 全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
 (2010全国卷2文数)(16)已知球
(2010全国卷2文数)(16)已知球 的半径为4,圆
的半径为4,圆 与圆
与圆 为该球的两个小圆,
为该球的两个小圆, 为圆
为圆 与圆
与圆 的公共弦,
的公共弦, ,若
,若 ,则两圆圆心的距离
,则两圆圆心的距离 。
。
[解析]3:本题考查球、直线与圆的基础知识
∵ ON=3,球半径为4,∴小圆N的半径为 ,∵小圆N中弦长AB=4,作NE垂直于AB,∴ NE=
,∵小圆N中弦长AB=4,作NE垂直于AB,∴ NE= ,同理可得
,同理可得 ,在直角三角形ONE中,∵
NE=
,在直角三角形ONE中,∵
NE= ,ON=3,∴
,ON=3,∴  ,∴
,∴ 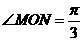 ,∴ MN=3
,∴ MN=3
(2010山东文数)(16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l: 被该圆所截得的弦长为
被该圆所截得的弦长为 ,则圆C的标准方程为
.
,则圆C的标准方程为
.
答案:
(2010四川理数)(14)直线 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 .
.
解析:方法一、圆心为(0,0),半径为2
圆心到直线 的距离为d=
的距离为d=


 w_w w. k#s5_
w_w w. k#s5_
故 w_w_w.k*s 5*
w_w_w.k*s 5*
得|AB|=2
答案:2
(2010天津文数)(14)已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切。则圆C的方程为 。
[答案]
本题主要考查直线的参数方程,圆的方程及直线与圆的位置关系等基础知识,属于容易题。
令y=0得x=-1,所以直线x-y+1=0,与x轴的交点为(-1.0)
因为直线与圆相切,所以圆心到直线的距离等于半径,即 ,所以圆C的方程为
,所以圆C的方程为
[温馨提示]直线与圆的位置关系通常利用圆心到直线的距离或数形结合的方法求解。
7.(2010上海文数)圆 的圆心到直线
的圆心到直线 的距离
的距离 3 。
3 。
解析:考查点到直线距离公式
圆心(1,2)到直线 距离为
距离为
21.(本小题满分13分)
数列 中,
中, 是函数
是函数 的极小值点
的极小值点
(Ⅰ)当a=0时,求通项 ;
;
(Ⅱ)是否存在a,使数列 是等比数列?若存在,求a的取值范围;若不存在,请说明理由。
是等比数列?若存在,求a的取值范围;若不存在,请说明理由。
20.

 (本小题满分13分)
(本小题满分13分)
已知函数 对任意的
对任意的 ,恒有
,恒有

 。
。
(Ⅰ)证明:当 时,
时, ;
;
(Ⅱ)若对满足题设条件的任意b,c,不等式 恒成立,求M的最小值。
恒成立,求M的最小值。
19.(本小题满分13分)
为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地。视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的的垂直平分线为y轴建立平面直角坐标系(图6)在直线x=2的右侧,考察范围为到点B的距离不超过 km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过
km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过 km区域。
km区域。
(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图6所示,设线段P1P2,P2P3是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间。


18.(本小题满分12分)
如图5所示,在正方体 E是棱
E是棱 的中点。
的中点。
(Ⅰ)求直线BE的平面 所成的角的正弦值;
所成的角的正弦值;
(II)在棱 上是否存在一点F,使
上是否存在一点F,使 平面
平面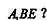 证明你的结论。
证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com