
题目列表(包括答案和解析)
(17)(本小题满分12分)
已知函数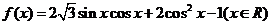
(Ⅰ)求函数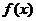 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若 ,求
,求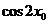 的值。
的值。
(18).(本小题满分12分)
某射手每次射击击中目标的概率是 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(Ⅰ)假设这名射手射击5次,求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次,求有3次连续击中目标。另外2次未击中目标的概率;
(Ⅲ)假设这名射手射击3次,每次射击,击中目标得1分,未击中目标得0分,在3次射击中,若有2次连续击中,而另外1次未击中,则额外加1分;若3次全击中,则额外加3分,记 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求 的分布列。
的分布列。
(19)(本小题满分12分)
 如图,在长方体
如图,在长方体 中,
中, 、
、 分别是棱
分别是棱 ,
,
上的点, ,
,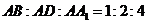
(1) 求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2) 证明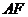
 平面
平面
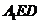
(3) 求二面角 的正弦值。
的正弦值。
(20)(本小题满分12分)
已知椭圆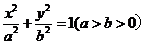 的离心率
的离心率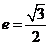 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(1) 求椭圆的方程;
(2) 设直线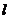 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点 的坐标为(
的坐标为(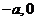 ),点
),点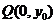 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且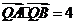 ,求
,求 的值
的值
(21)(本小题满分14分)
已知函数
(Ⅰ)求函数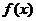 的单调区间和极值;
的单调区间和极值;
(Ⅱ)已知函数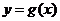 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,证明当
对称,证明当 时,
时,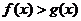
(Ⅲ)如果 ,且
,且 ,证明
,证明
(22)(本小题满分14分)
在数列 中,
中, ,且对任意
,且对任意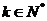 .
.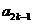 ,
, ,
, 成等差数列,其公差为
成等差数列,其公差为 。
。
(Ⅰ)若 =
= ,证明
,证明 ,
, ,
, 成等比数列(
成等比数列(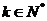 )
)
(Ⅱ)若对任意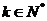 ,
, ,
, ,
, 成等比数列,其公比为
成等比数列,其公比为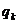 。
。
2010年普通高等学校招生全国统一考试(天津卷)
(11)甲、乙两人在10天中每天加工零件的个数用茎叶图表示如下图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数,则这10天甲、乙两人日加工零件的平均数分别为 和 。

(12)一个几何体的三视图如图所示,则这个几何体的体积为

(13)已知圆C的圆心是直线 与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为
与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为
(14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若 ,则
,则 的值为 。
的值为 。
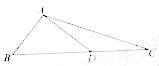 (15)如图,在
(15)如图,在 中,
中, ,
, ,
,
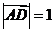 ,则
,则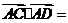 .
.
(16)设函数 ,对任意
,对任意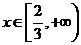 ,
, 恒成立,则实数
恒成立,则实数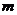 的取值范围是 .
的取值范围是 .
(17)(本小题满分12分)
在 ABC中,
ABC中, 。
。
(Ⅰ)证明B=C:
(Ⅱ)若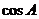 =-
=-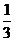 ,求sin
,求sin 的值。
的值。
(18)(本小题满分12分)
有编号为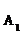 ,
, ,…
,… 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
 其中直径在区间[1.48,1.52]内的零件为一等品。
其中直径在区间[1.48,1.52]内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率。
(19)(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD= ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
(20)(本小题满分12分)
已知函数f(x)= ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间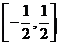 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
(21)(本小题满分14分)
已知椭圆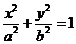 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(-a,0).
(i)若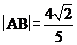 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 .求
.求 的值.
的值.
(22)(本小题满分14分)
在数列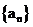 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,其公差为2k.
成等差数列,其公差为2k.
(Ⅰ)证明 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)记 ,证明
,证明 .
.
2010年普通高等学校招生全国统一考试(天津卷)
(11)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P。若PB=1,PD=3,则 的值为 。
的值为 。
(12)一个几何体的三视图如图所示,则这个几何体的体积为 。
 (13)已知双曲线
(13)已知双曲线 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点相同。则双曲线的方程为
。
的焦点相同。则双曲线的方程为
。
(14)已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切。则圆C的方程为 。
(15)设{an}是等比数列,公比 ,Sn为{an}的前n项和。记
,Sn为{an}的前n项和。记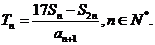 设
设 为数列{
为数列{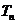 }的最大项,则
}的最大项,则 =
。
=
。
(16)设函数f(x)=x- ,对任意x
,对任意x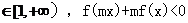 恒成立,则实数m的取值范围是________
恒成立,则实数m的取值范围是________
(15)(本小题共13分)
已知函数
 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值。
的最大值和最小值。
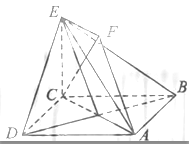
(16)(本小题共14分)
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
(17)(本小题共13分)
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为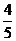 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为 ,
,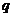 (
( >
>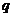 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
 |
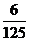 |
 |
 |
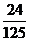 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求 ,
,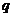 的值;
的值;
(Ⅲ)求数学期望 ξ。
ξ。
(18)(本小题共13分)
已知函数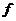 (
( )=In(1+
)=In(1+ )-
)- +
+ (
( ≥0)。
≥0)。
(Ⅰ)当 =2时,求曲线
=2时,求曲线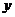 =
=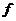 (
( )在点(1,
)在点(1,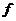 (1))处的切线方程;
(1))处的切线方程;
(Ⅱ)求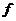 (
( )的单调区间。
)的单调区间。
(19)(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
(20)(本小题共13分)
已知集合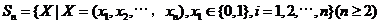 对于
对于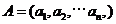 ,
,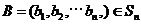 ,定义A与B的差为
,定义A与B的差为

A与B之间的距离为
(Ⅰ)证明: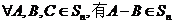 ,且
,且 ;
;
(Ⅱ)证明: 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅲ) 设P ,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为
,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为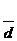 (P).
(P).
证明: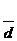 (P)≤
(P)≤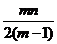 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
()
2010年普通高等学校招生全国统一考试
(9)在复平面内,复数 对应的点的坐标为
。
对应的点的坐标为
。
(10)在△ABC中,若b = 1,c = ,
,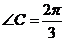 ,则a =
。
,则a =
。
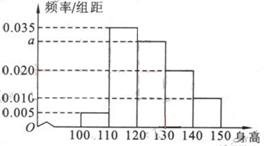 (11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。
(11)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图)。由图中数据可知a=
。若要从身高在[ 120 , 130),[130 ,140) , [140 , 150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140 ,150]内的学生中选取的人数应为
。

(12)如图, 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD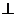 AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
 (13)已知双曲线
(13)已知双曲线 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆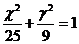 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
(14)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是 ,则
,则 的最小正周期为
;
的最小正周期为
; 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿 轴滚动”包括沿
轴滚动”包括沿 轴正方向和沿
轴正方向和沿 轴负方向滚动。沿
轴负方向滚动。沿 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿 轴负方向滚动。
轴负方向滚动。
(1) 集合 ,则
,则 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
(2)在等比数列 中,
中, ,公比
,公比 .若
.若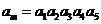 ,则m=
,则m=
(A)9 (B)10 (C)11 (D)12
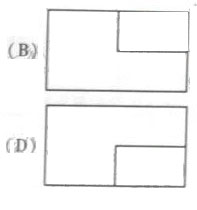
 (3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为

(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为
(A) (B)
(B)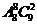 (C)
(C)
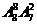 (D)
(D)
(5)极坐标方程(p-1)( )=(p
)=(p 0)表示的图形是
0)表示的图形是
(A)两个圆 (B)两条直线
(C)一个圆和一条射线 (D)一条直线和一条射线
(6)a、b为非零向量。“ ”是“函数
”是“函数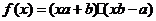 为一次函数”的
为一次函数”的
(A)充分而不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)设不等式组  表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y= 的图像上
的图像上
存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2]
(D )[ 3, 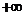 ]
]
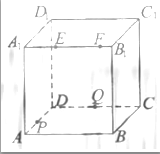 (8)如图,正方体ABCD-
(8)如图,正方体ABCD- 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱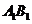 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1, E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关
(B)与x有关,与y,z无关
(C)与y有关,与x,z无关
(D)与z有关,与x,y无关
第II卷(共110分)
(13)设 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有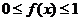 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分 ,先产生两组(每组N个)区间
,先产生两组(每组N个)区间 上的均匀随机数
上的均匀随机数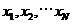 和
和 ,由此得到N个点
,由此得到N个点 ,再数出其中满足
,再数出其中满足 的点数
的点数 ,那么由随机模拟方案可得积分
,那么由随机模拟方案可得积分 的近似值为 。
的近似值为 。
(14)正视图为一个三角形的几何体可以是______(写出三种)
(15)过点A(4,1)的圆C与直线x-y=0相切于点B(2,1),则圆C的方程为____
(16)在△ABC中,D为边BC上一点,BD=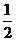 DC,
DC,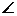 ADB=120°,AD=2,若△ADC的面积为
ADB=120°,AD=2,若△ADC的面积为 ,则
,则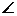 BAC=_______
BAC=_______
三,解答题:解答应写出文字说明,正明过程和演算步骤
(17)(本小题满分12分)
设数列 满足
满足
(1)
求数列 的通项公式;
的通项公式;
(2)
 令
令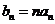 ,求数列的前n项和
,求数列的前n项和
(18)(本小题满分12分)
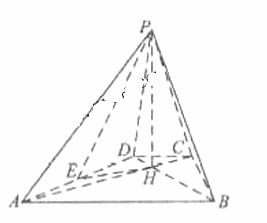
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB CD,AC
CD,AC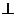 BD,垂足为H,PH是四棱锥的高 ,E为AD中点
BD,垂足为H,PH是四棱锥的高 ,E为AD中点
(1)
证明:PE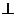 BC
BC
(2)
若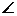 APB=
APB=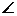 ADB=60°,求直线PA与平面PEH所成角的正弦值
ADB=60°,求直线PA与平面PEH所成角的正弦值
(19)(本小题12分)
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
|
是否需要志愿 性别 |
男 |
女 |
|
需要 |
40 |
30 |
|
不需要 |
160 |
270 |
(1) 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2) 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3) 根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
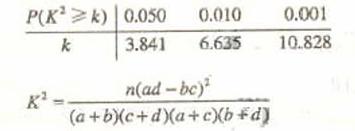 附:
附:
(20)(本小题满分12分)
设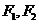 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 斜率为1的直线
斜率为1的直线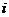 与
与 相交于
相交于 两点,且
两点,且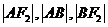 成等差数列。
成等差数列。
(1)求 的离心率;
的离心率;
(2) 设点 满足
满足 ,求
,求 的方程
的方程
(21)(本小题满分12分)
设函数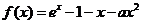 。
。
(1)
若 ,求
,求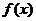 的单调区间;
的单调区间;
(2) 若当 时
时 ,求
,求 的取值范围
的取值范围
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,已经圆上的弧 ,过C点的圆切线与BA的延长线交于E点,证明:
,过C点的圆切线与BA的延长线交于E点,证明:
(Ⅰ)∠ACE=∠BCD;
(Ⅱ)BC2=BF×CD。

(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知直线C1 (t为参数),C2
(t为参数),C2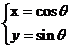 (
( 为参数),
为参数),
(Ⅰ)当 =
=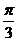 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为 ,P为OA中点,当
,P为OA中点,当 变化时,求P点的轨迹的参数方程,并指出它是什么曲线。
变化时,求P点的轨迹的参数方程,并指出它是什么曲线。
(24)(本小题满分10分)选修4-5,不等式选项
设函数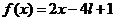
(Ⅰ)画出函数 的图像
的图像
(Ⅱ)若不等式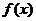 ≤
≤ 的解集非空,求a的取值范围。
的解集非空,求a的取值范围。

2010年普通高等学校招生全国统一考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com