3、(2010江西理数)6. 展开式中不含项的系数的和为(　 )

A.-1　　　　 B.0　　　　 C.1　　　　 D.2

[答案]B

[解析]考查对二项式定理和二项展开式的性质，重点考查实践意识和创新能力，体现正难则反。采用赋值法，令x=1得：系数和为1，减去项系数即为所求，答案为0.

2、(2010全国卷2文数)(9)将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有

(A) 12种　　　 (B) 18种　　　 (C) 36种　　　　 (D) 54种

[解析]B：本题考查了排列组合的知识

∵先从3个信封中选一个放1，2有3种不同的选法，再从剩下的4个数中选两个放一个信封有，余下放入最后一个信封，∴共有

1、(2010全国卷2理数)(6)将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中．若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有

(A)12种　　　　　 (B)18种　　　　　 (C)36种　　　　　 (D)54种

[答案]B

[命题意图]本试题主要考察排列组合知识，考察考生分析问题的能力.

[解析]标号1,2的卡片放入同一封信有种方法；其他四封信放入两个信封，每个信封两个有种方法，共有种，故选B.

46、(2010全国卷2理数)(17)(本小题满分10分)

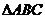中，为边上的一点，，，，求．

[命题意图]本试题主要考查同角三角函数关系、两角和差公式和正弦定理在解三角形中的应用，考查考生对基础知识、基本技能的掌握情况.

45、(2010浙江理数)(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c，已知

　 　　(I)求sinC的值；

(Ⅱ)当a=2， 2sinA=sinC时，求b及c的长．

解析：本题主要考察三角变换、正弦定理、余弦定理等基础知识，同事考查运算求解能力。

(Ⅰ)解：因为cos2C=1-2sin²C=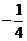，及0＜C＜π

所以sinC=.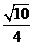

(Ⅱ)解：当a=2，2sinA=sinC时，由正弦定理，得

c=4

由cos2C=2cos²C-1=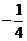，J及0＜C＜π得

cosC=±

由余弦定理c²=a²+b²-2abcosC，得

b²±b-12=0

所以　 b=　　　　　　 b=

　　　 c=4　　　 或　　　 c=4

44、(2010湖南文数)16. (本小题满分12分)

已知函数

(I)求函数的最小正周期。

(II)　 求函数的最大值及取最大值时x的集合。

43、(2010上海文数)19.(本题满分12分)

已知，化简：

.

解析：原式=lg(sinx+cosx)+lg(cosx+sinx)-lg(sinx+cosx)²=0．

42、(2010江苏卷)13、在锐角三角形ABC，A、B、C的对边分别为a、b、c，，则=____▲_____。

[解析] 考查三角形中的正、余弦定理三角函数知识的应用，等价转化思想。一题多解。

(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。

当A=B或a=b时满足题意，此时有：，，，

，= 4。

(方法二)，

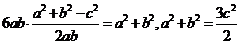
41、(2010江苏卷)10、定义在区间上的函数y=6cosx的图像与y=5tanx的图像的交点为P，过点P作PP₁⊥x轴于点P₁，直线PP₁与y=sinx的图像交于点P₂,则线段P₁P₂的长为_______▲_____。

[解析] 考查三角函数的图象、数形结合思想。线段P₁P₂的长即为sinx的值，

且其中的x满足6cosx=5tanx，解得sinx=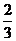。线段P₁P₂的长为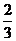

40、(2010福建理数)14．已知函数和的图象的对称轴完全相同。若，则的取值范围是　　　　 。

[答案]

[解析]由题意知，，因为，所以，由三角函数图象知：

的最小值为，最大值为，所以的取值范围是。