
题目列表(包括答案和解析)
5.A
[解析]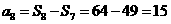 .
.
[方法技巧]直接根据 即可得出结论.
即可得出结论.
8、(2010安徽文数)(5)设数列 的前n项和
的前n项和 ,则
,则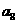 的值为
的值为
(A) 15 (B) 16 (C) 49 (D)64
7、(2010江西理数)4.  ( )
( )
A.  B.
B.  C. 2 D. 不存在
C. 2 D. 不存在
[答案]B
[解析]考查等比数列求和与极限知识.解法一:先求和,然后对和取极限。
6、(2010江西理数)5.等比数列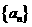 中,
中,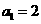 ,
,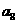 =4,函数
=4,函数
 ,则
,则 ( )
( )
A. B.
B. 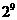 C.
C.  D.
D. 
[答案]C
[解析]考查多项式函数的导数公式,重点考查学生创新意识,综合与灵活地应用所学的数学知识、思想和方法。考虑到求导中,含有x项均取0,则 只与函数
只与函数 的一次项有关;得:
的一次项有关;得: 。
。
5、(2010全国卷2文数)(6)如果等差数列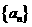 中,
中,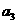 +
+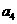 +
+ =12,那么
=12,那么 +
+ +•••…+
+•••…+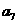 =
=
(A)14 (B) 21 (C) 28 (D) 35
[解析]C:本题考查了数列的基础知识。
∵  ,∴
,∴ 

4、(2010辽宁理数)(6)设{an}是有正数组成的等比数列, 为其前n项和。已知a2a4=1,
为其前n项和。已知a2a4=1, 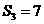 ,则
,则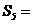
(A)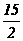 (B)
(B) (C)
(C) (D)
(D)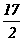
[答案]B
[命题立意]本题考查了等比数列的通项公式与前n项和公式,考查了同学们解决问题的能力。
[解析]由a2a4=1可得 ,因此
,因此 ,又因为
,又因为 ,联力两式有
,联力两式有 ,所以q=
,所以q=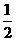 ,所以
,所以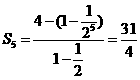 ,故选B。
,故选B。
3、(2010辽宁文数)(3)设 为等比数列
为等比数列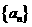 的前
的前 项和,已知
项和,已知 ,
,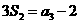 ,则公比
,则公比
(A)3 (B)4 (C)5 (D)6
解析:选B. 两式相减得,  ,
, .
.
2、(2010全国卷2理数)(4).如果等差数列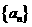 中,
中, ,那么
,那么
(A)14 (B)21 (C)28 (D)35
[答案]C
[命题意图]本试题主要考查等差数列的基本公式和性质.
[解析]
1、(2010浙江理数)(3)设 为等比数列
为等比数列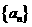 的前
的前 项和,
项和, ,则
,则
(A)11 (B)5
(C) (D)
(D)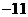
解析:解析:通过 ,设公比为
,设公比为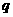 ,将该式转化为
,将该式转化为 ,解得
,解得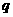 =-2,带入所求式可知答案选D,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式,属中档题
=-2,带入所求式可知答案选D,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式,属中档题
5、 设二次函数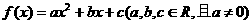 满足条件:
满足条件:
(1)当 时,
时,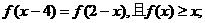
(2)当 ;
;
(3) 在R上的最小值为0.
在R上的最小值为0.
则 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com