
题目列表(包括答案和解析)
19 (12分)已知向量
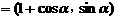 ,
,
 ,
, = (1,0),其中
= (1,0),其中 ,
,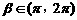 若
若 与
与 的夹角为
的夹角为 ,
, 与
与 的夹角为
的夹角为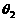 ,且
,且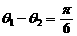 ,求
,求 的值
的值
 20 (12分)如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC = 90°,BE和CD都垂直于平面ABC,且BE = AB
= 2,CD = 1,点F是AE的中点
20 (12分)如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC = 90°,BE和CD都垂直于平面ABC,且BE = AB
= 2,CD = 1,点F是AE的中点
(1)求证:DF∥平面ABC;
(2)求AB与平面BDF所成角的大小
21 (14分)已知数列{an}的各项均为正数且a1 = 6,点 在抛物线
在抛物线 上;数列{bn}中,点
上;数列{bn}中,点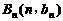 在过点(0,1)且方向向量为(1,2)的直线上
在过点(0,1)且方向向量为(1,2)的直线上
(1)求数列{an} {bn}的通项公式;
(2)对任意正整数n,不等式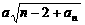 ≤
≤ …
…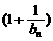 成立,求正数a的取值范围
成立,求正数a的取值范围
22 (14分)已知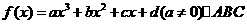 是定义在R上的函数,其图象交x轴于A、B、C三点 若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求| AC |的取值范围
是定义在R上的函数,其图象交x轴于A、B、C三点 若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求| AC |的取值范围
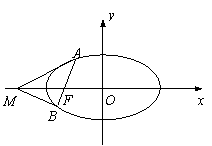 23 (14分)如图,过椭圆
23 (14分)如图,过椭圆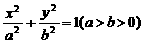 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”
(1)求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”
(1)求椭圆 的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆
 的“左特征点”M是一个怎样的点?并证明你的结论
的“左特征点”M是一个怎样的点?并证明你的结论
13 已知 ,
, 是两个不共线的向量,
是两个不共线的向量, = k2
= k2 + (
+ (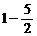 k)
k)  和
和 = 2
= 2 + 3
+ 3 是两个共线向量,则实数k =
是两个共线向量,则实数k =
 14 正方体
14 正方体 中,与
中,与 异面,且与
异面,且与 所成角为
所成角为 的面对角线共有 条
的面对角线共有 条
 15 将大小不同的两种钢板截成A B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示 现在需要A
B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张
15 将大小不同的两种钢板截成A B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示 现在需要A
B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张
16 若指数函数f(x)=ax (x∈R)的部分对
应值如右表:则不等式 (|x-1|)<0的
(|x-1|)<0的
解集为
17 在函数 中,若a,b,c成等比数列,且
中,若a,b,c成等比数列,且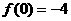 ,则
,则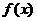 有最______值(填“大”或“小”),且该值为____________
有最______值(填“大”或“小”),且该值为____________
18 抛物线 上点P的纵坐标为
上点P的纵坐标为 ,则P点到焦点F的距离为____
,则P点到焦点F的距离为____
1 若非空数集A = {x|2a + 1≤x≤3a-5 },B = {x|3≤x≤22 },则能使 成立的所有a的集合是
( )
成立的所有a的集合是
( )
A {a|1≤a≤9} B
{a|6≤a≤9} C {a|a≤9} D 
2 不等式 的解集是
( )
A
{x︱x>
的解集是
( )
A
{x︱x> } B {x︱x<
} B {x︱x< }
C {x︱
}
C {x︱ <x<1或x>1} D {x|x<
<x<1或x>1} D {x|x< 或x>1}
或x>1}
3 若点P(3,4) Q(a,b)关于直线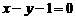 对称,则
( )
A
a = 1,b =
对称,则
( )
A
a = 1,b = B a = 2,b =
B a = 2,b = 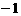 C a = 4,b = 3 D a = 5,b = 2
C a = 4,b = 3 D a = 5,b = 2
4 一质点在直角坐标平面上沿直线匀速行进,上午7时和9时该动点的坐标依次为 和
和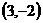 ,则下午5时该点的坐标是
( )
,则下午5时该点的坐标是
( )
A (9,11) B (11,-16) C (11,-18) D (13,-16)
5 已知直线m n,平面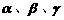 ,则
,则 的一个充分不必要条件为( )
A
的一个充分不必要条件为( )
A  B
B 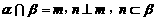 C
C  D
D 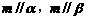
6 抛物线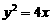 按向量
按向量 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为 A
(4,2) B
(2,2) C
(-2,-2)
D (2,3) ( )
平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为 A
(4,2) B
(2,2) C
(-2,-2)
D (2,3) ( )
7 设a、b、c都是正数,那么三个数

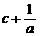 ( )
A
都不大于2 B 都不小于2
C
至少有一个不大于2 D 至少有一个不小于2
( )
A
都不大于2 B 都不小于2
C
至少有一个不大于2 D 至少有一个不小于2
8 已知椭圆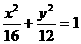 的左焦点是
的左焦点是 ,右焦点是
,右焦点是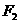 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
( )
轴上,那么
( )
A 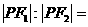
 B
B 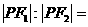
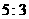
C 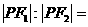
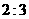 D
D 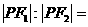
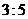
9 点P在直径为 的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是
( )
A
的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是
( )
A
 B 6 C
B 6 C  D
D 
10 已知函数 在区间(
在区间( ,1)上有最小值,则函数
,1)上有最小值,则函数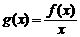 在区间(1,
在区间(1, 上一定
( )
A
有最小值 B 有最大值 C 是减函数 D 是增函数
上一定
( )
A
有最小值 B 有最大值 C 是减函数 D 是增函数
11 已知函数f (x)的定义域为[a,b],函数f (x)的图象如右图所示,
则函数f (| x |)的图象是 ( )

A B C D
 12 定义域和值域均为
12 定义域和值域均为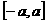 (常数
(常数 )的函数
)的函数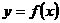 和
和 的图像如图所示,给出下列四个命题:
的图像如图所示,给出下列四个命题:
①方程 有且仅有三个解;
有且仅有三个解;
②方程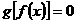 有且仅有三个解;
有且仅有三个解;
③方程 有且仅有九个解;
有且仅有九个解;
④方程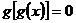 有且仅有一个解
有且仅有一个解
那么,其中正确命题的个数是 ( )
(A)①② (B)②③ (C)③④ (D)④①
17 (本小题满分12分)设向量 =(cos23°,cos67°),
=(cos23°,cos67°),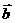 b=(cos68°,cos22°),
b=(cos68°,cos22°), (t∈R) (1)求
(t∈R) (1)求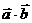 ;(2)求
;(2)求 u的模的最小值
u的模的最小值
18 (本小题满分12分)
(理)某系统是由四个整流二极管(串 并)联结而成,已知每个二极管的可靠度为0.8
(即正常工作时),若要求系统的可靠度大于0 . 85,请你设计至少两种不同的联结方式,并说明理由
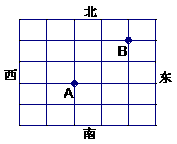 (文)如图是一个方格迷宫,甲
乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、 南、北四个方向之一行走 若甲向东、向西行走的概率均为
(文)如图是一个方格迷宫,甲
乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、 南、北四个方向之一行走 若甲向东、向西行走的概率均为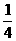 ,向南 、向北行走的概率分别为
,向南 、向北行走的概率分别为 和p,乙向东、南 、 西 、 北四个方向行走的概率均为q
和p,乙向东、南 、 西 、 北四个方向行走的概率均为q
(1)求p和q的值;
(2)设至少经过t分钟,甲 、乙两人能首次相遇,试确定t的值,并求t分钟时,甲乙两人相遇的概率
19 (本小题满分12分)
(理)已知函数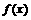 、
、 对任意实数
对任意实数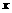 、
、 分别满足
分别满足
① 且
且 ;②
;②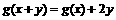 且
且 ,
, 为正整数
为正整数
(1)求数列 、
、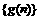 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和
(文)已知等比数列 ,
,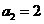 ,
,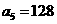
(1)求通项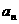 ;
;
(2)若 ,数列
,数列 的前
的前 项的和为
项的和为 ,且
,且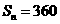 ,求
,求 的值
的值
20 (本小题满分12分)如图,在底面是菱形的四棱锥P-ABCD中,
∠ABC=600,PA=AC=a,PB=PD=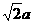 ,点E在PD上,且PE:ED=2:1
,点E在PD上,且PE:ED=2:1
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角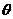 的大小;
的大小;
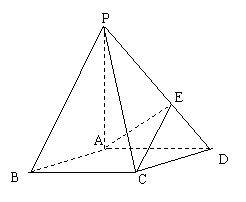 (3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论
21 (本小题满分12分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、 B(0,-2),点C满足 、
、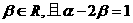
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线 交于两点M N,且以MN为直径的圆过原点,求证:
交于两点M N,且以MN为直径的圆过原点,求证:
22 (本小题满分14分)
(理)已知函数
(1)求函数 的最大值;
的最大值;
(2)当 时,求证
时,求证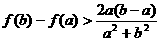
(文)设函数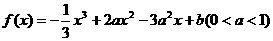
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈[a+1, a+2]时,不等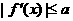 ,求a的取值范围
,求a的取值范围
19.已知函数 .
.
(1) 设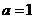 ,求函数
,求函数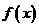 的极值;
的极值;
(2) 若 ,且当
,且当 时,
时,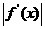
 12a恒成立,试确定
12a恒成立,试确定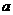 的取值范围.
的取值范围.
18.已知椭圆 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个项点到两个焦点的距离分别是7和1.
轴上,它的一个项点到两个焦点的距离分别是7和1.
(I)
求椭圆 的方程;
的方程;
(II) 若 为椭圆
为椭圆 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,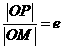 (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
17.某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
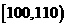 |
 |
 |
 |
 |
|
人数 |
4 |
8 |
 |
5 |
3 |
表2:
|
生产能力分组 |
 |
 |
 |
 |
|
人数 |
6 |
y |
36 |
18 |
(1) 先确定 ,并完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,并完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)

(ii)分别估计 类工人和
类工人和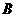 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
16.如图,在三棱锥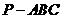 中,⊿
中,⊿ 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
(Ⅰ)证明:AB⊥PC
 (Ⅱ)若
(Ⅱ)若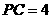 ,且平面
,且平面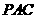 ⊥平面
⊥平面 , 求三棱锥
, 求三棱锥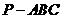 体积。
体积。
15.如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
, ,于A处测得水深
,于A处测得水深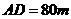 ,于B处测得水深
,于B处测得水深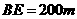 ,于C处测得水深
,于C处测得水深
 ,求∠DEF的余弦值。
,求∠DEF的余弦值。
14. 如图,正方体 的棱线长为1,线段
的棱线长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是
.
,则下列结论中错误的是
.
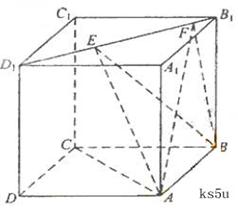 (A)
(A)
(B)
(C)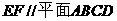
(D)三棱锥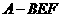 的体积为定值
的体积为定值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com